组合逻辑电路
三态门
有关于三态门:
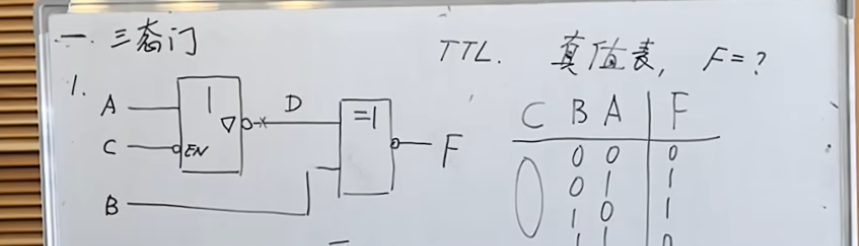
要求写出上面电路的真值表,并计算出
NOTE
三态门:
当
当
CMOS 中,如果三态门的使能端是
所以结果为当
得到真值表的结果为:

然后再看当
真值表得到是:
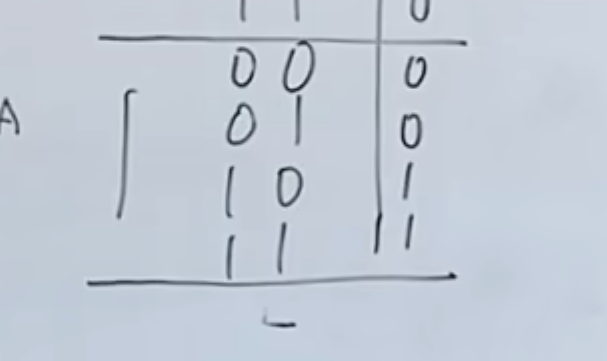
综合起来得到:
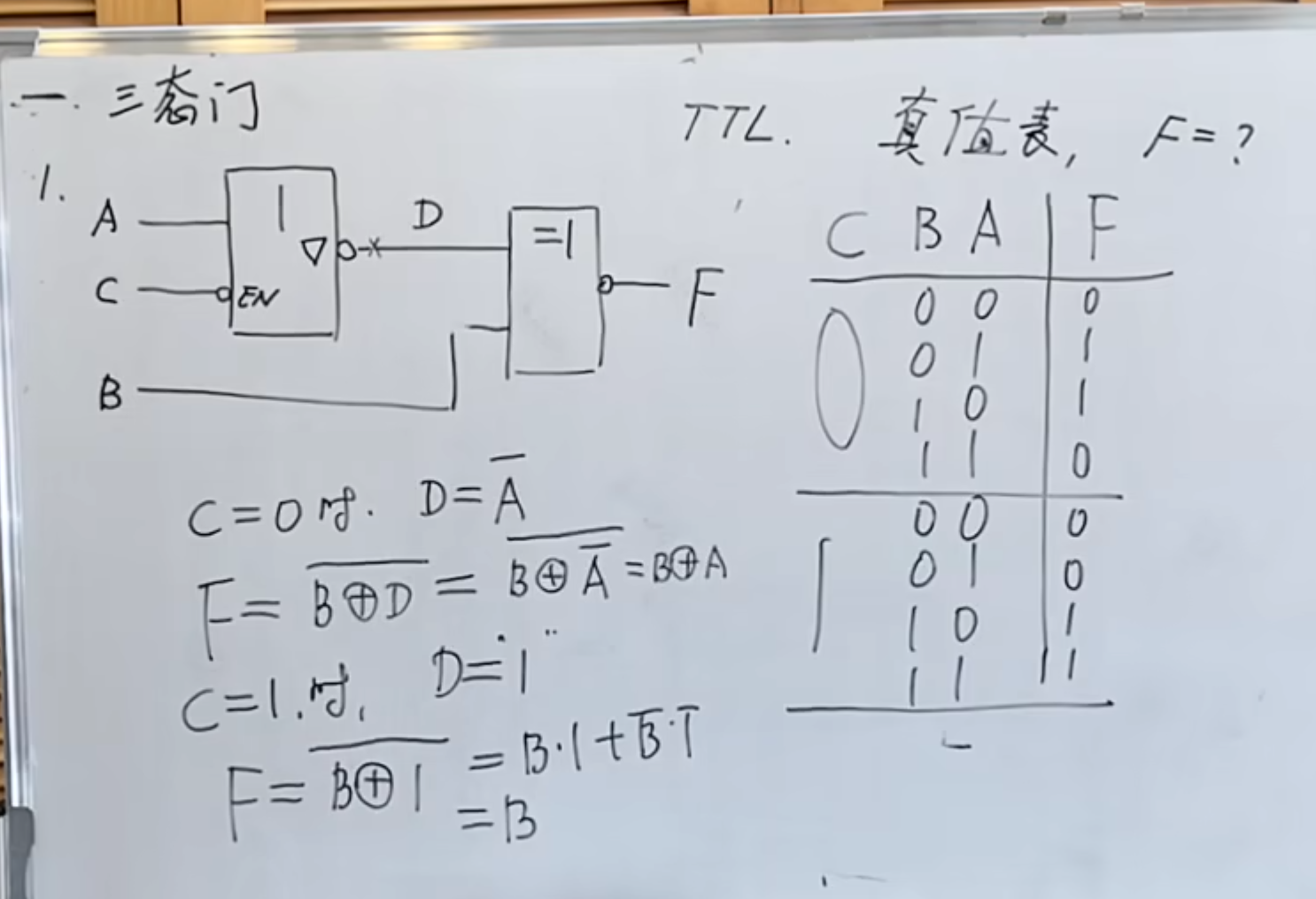
然后是计算得到
方法可以使用卡诺图的方法来得到:
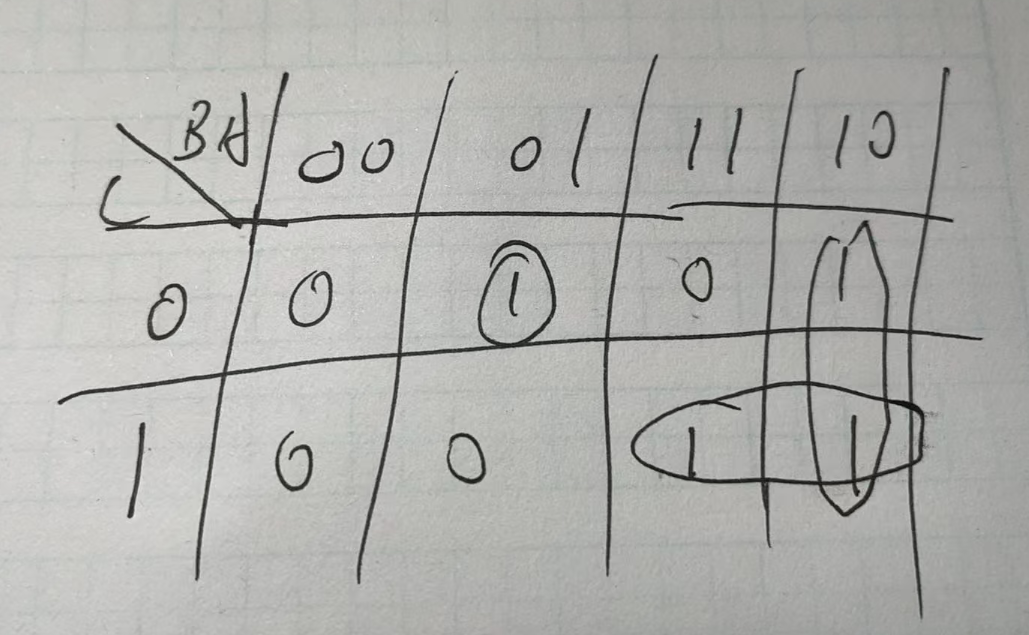
NOTE
需要注意的是变量的顺序,一定要按照真值表上的顺序来画卡诺图!
得到结果为:
三态门的第二个题:
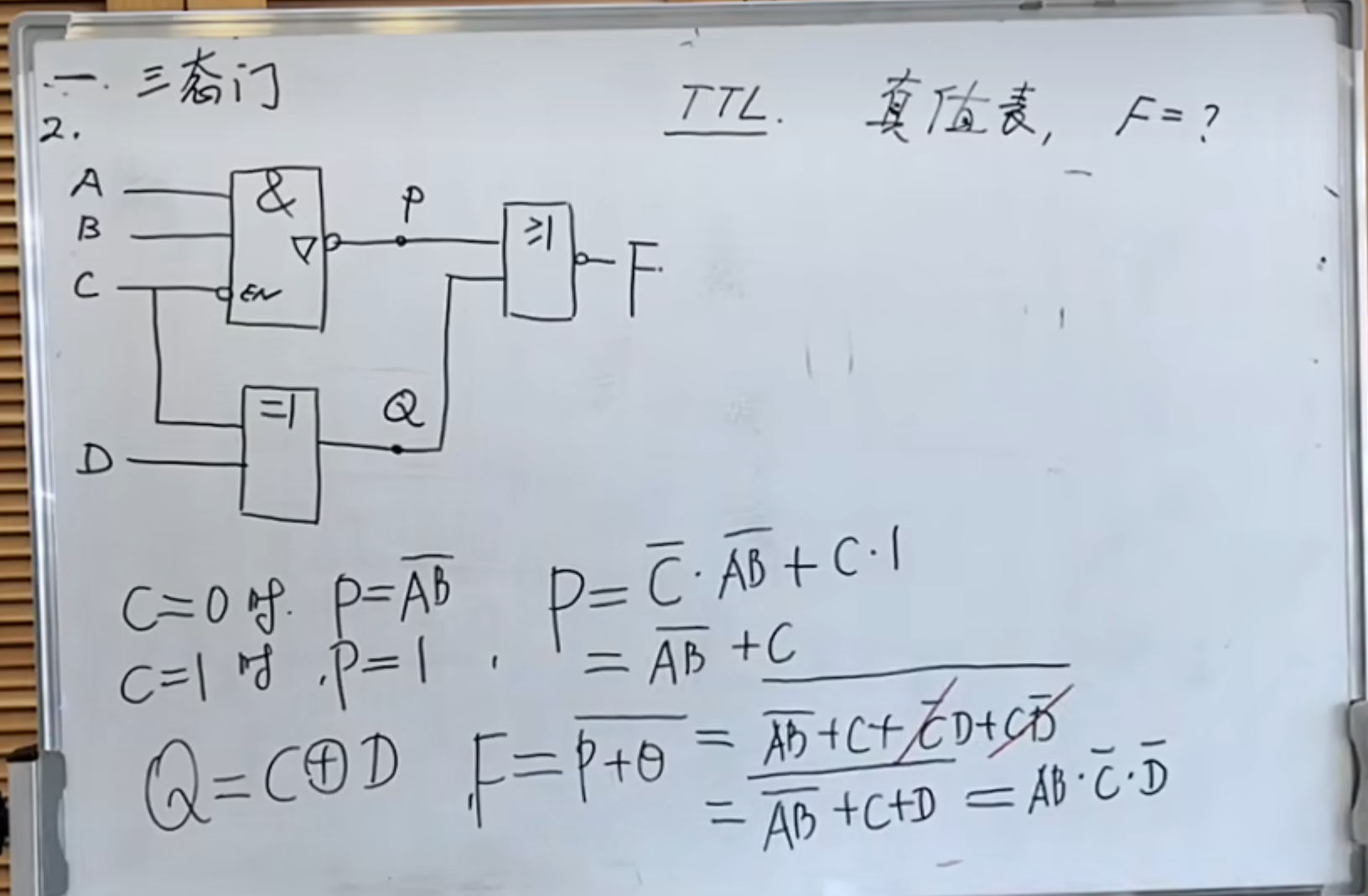
这个题当然可以使用真值表的方法计算得到,除此之外,可以使用逻辑表达式分析化简的方法来得到最后的结果。
首先看
这个时候可以得到 P 的表达式:
原因是要分析
NOTE
除了这里的与非门之外,如果换成别的门当然也可以使用同样的方式来分析。
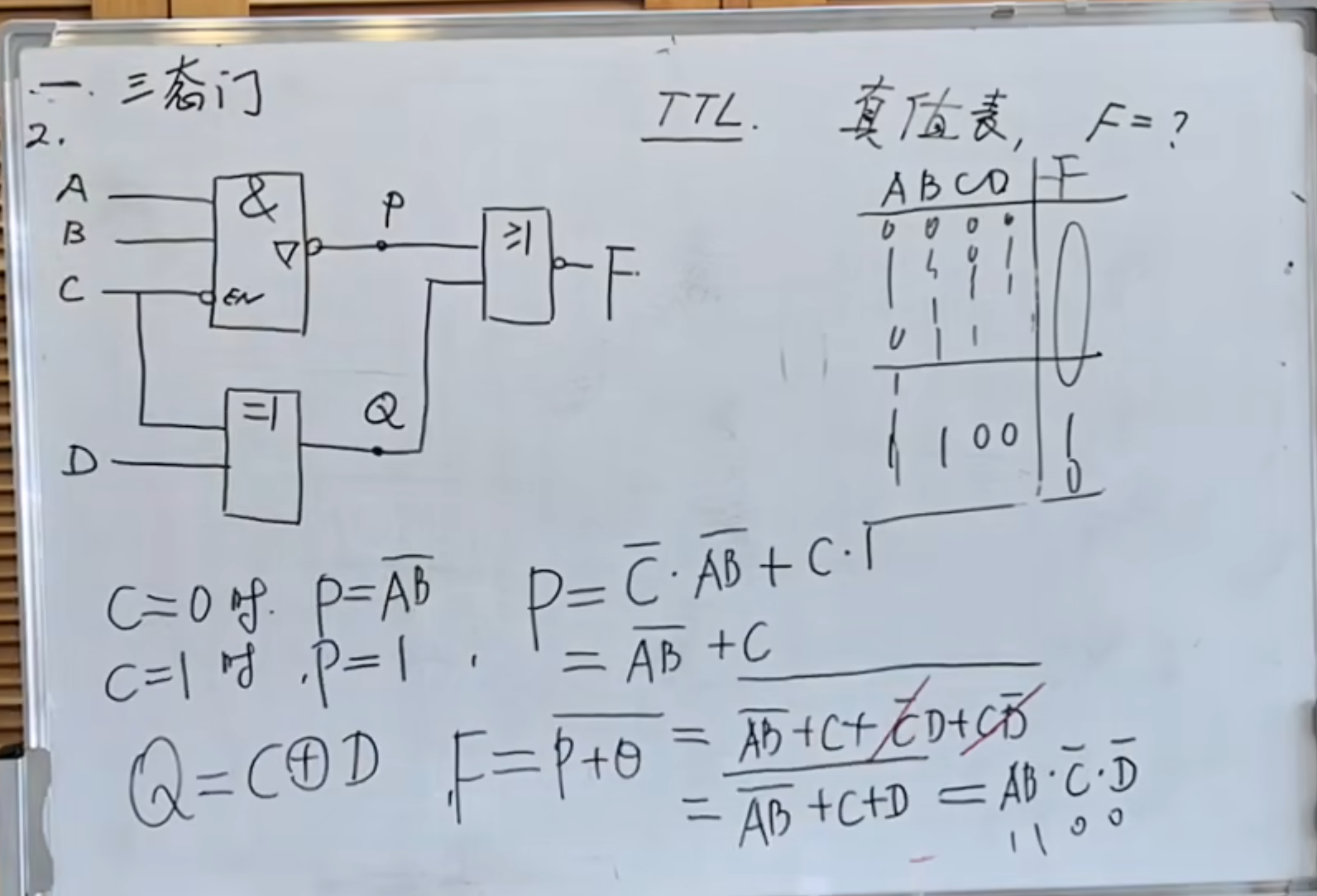
有关三态门的第三个题
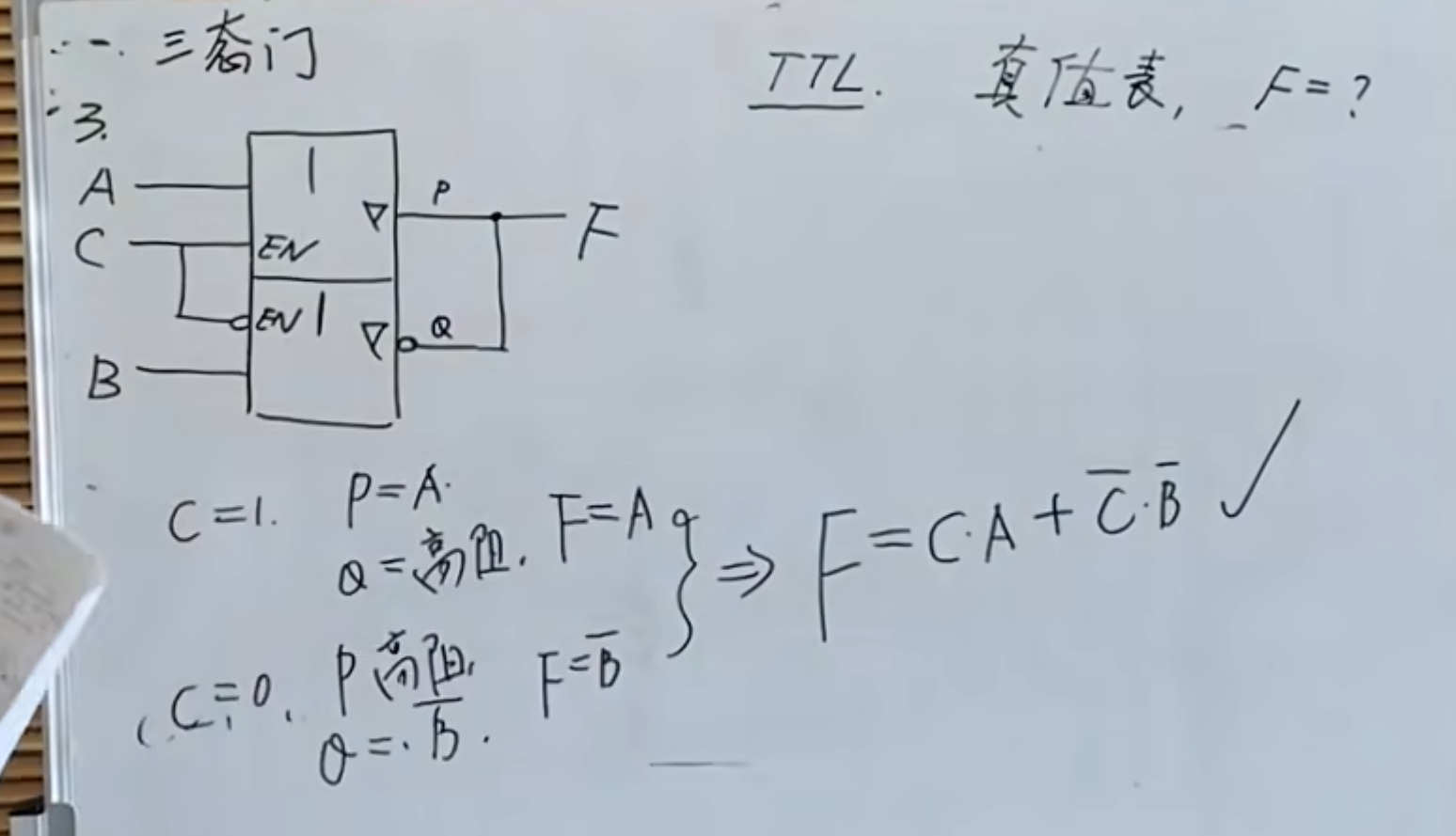
NOTE
注意后面的线与
线与只有在 OC\OD 门与三态门中可以使用,相当于与门
这里的分析依然是根据逻辑表达式的方法来计算的,当然如果使用真值表的方法也可以,但是会比较慢。
有关三态门的第四个题:
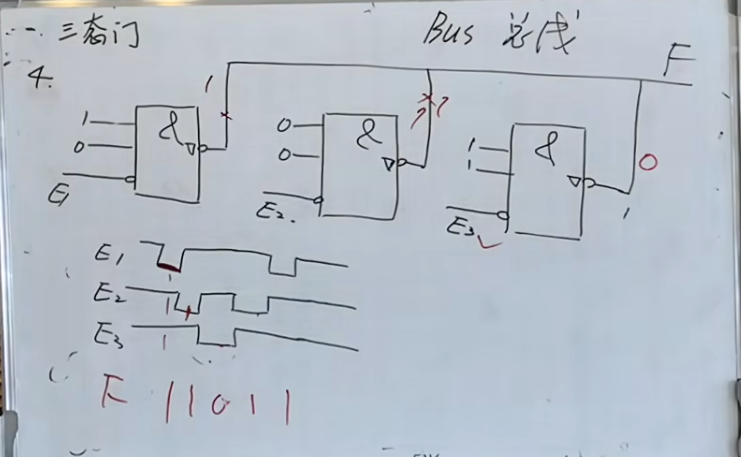
这里主要用的知识点是总线
NOTE
总线的含义是同一个时刻,只能有一个部分的值在总线上,也就是当第一部分有效的时候,其他几个部分必须是无效的,或者是高阻的
组合逻辑电路的竞争冒险
竞争冒险的第一个题:

具体方法就是用卡诺图来判断。
直接展示正确答案的卡诺图:
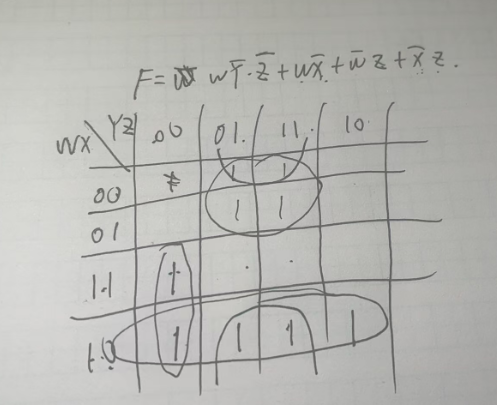
NOTE
尽管上面这部分有相切的部分,但是每个圈之间都有另外一个圈将他们连接起来,这样就消除了竞争冒险
竞争冒险第二个题

其使用的方法依然是卡诺图分析
下面这个题是电路分析题:
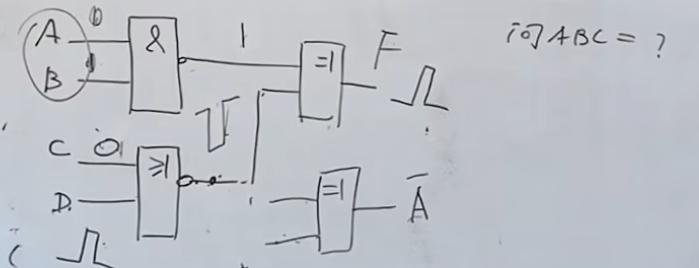
问题是,当
问题可以换成想要
NOTE
脉冲与单独
首先是当
从后往前分析,首先是 F 之前的异或门,这里要清晰知道异或门的反相器性质
在知道这个性质之后,首先来判断,当异或门上面的第一个输入为
或:有 1 为 1,全 0 为 0.
很明显,因为
所以这个时候就要改变异或门的第一个输入,让这个输入为
而,上面的
与:有 0 为 0,全 1 为 1.
然后来看 C:
由于当
那么反过来看当
那么这个时候
NOTE
这里其实是对或非门性质的理解。在或非门的输入中,当有一个输入为
所以结果就是:
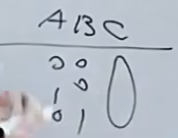
将题目稍微变换一下:
当
在上面的分析中已经提到,对于或非门,
而此时,当
再经过反相器,只需要不让反相器工作,也就是另外一个输入为
而只有当
所以结果为:
组合逻辑电路的设计

题目:有三个车间,每个车间的耗电功率如图上所示。还有两个配电站,提供的功率如图上所示。问题是设计一个供电控制电路,使其最节能。
具体解题步骤是
首先将对象抽象出来,然后将真值表画出来:
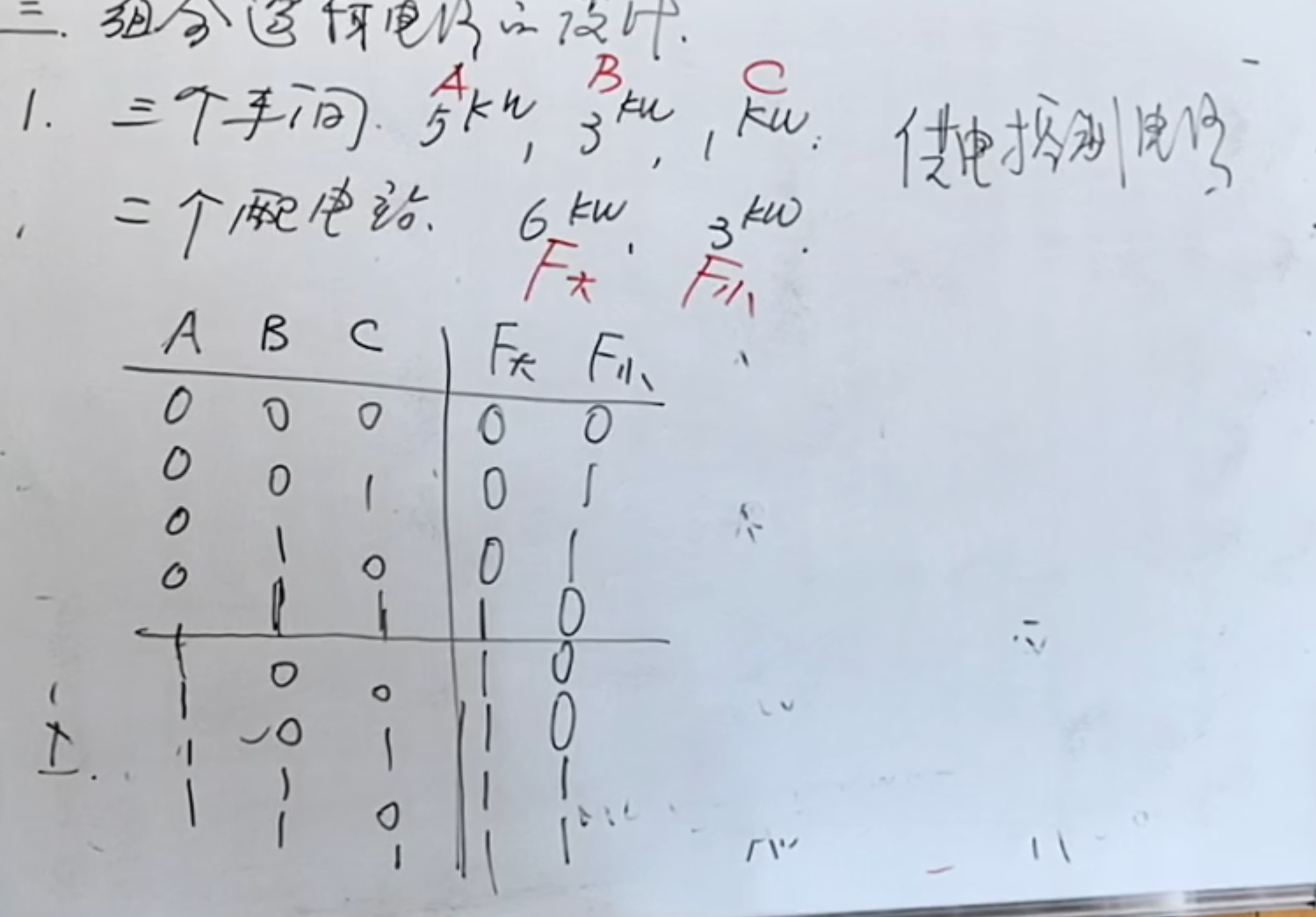
然后就是使用卡诺图化简,或者直接使用逻辑表达式化简。得到最后的结果。
第二个组合逻辑电路设计题:
设计一个由三处均可以控制灯的电路。
这里主要是抽象问题,在这里假设当输入发生一次改变的时候灯的状态也发生改变,初试状态为
那么真值表就可以画出来:
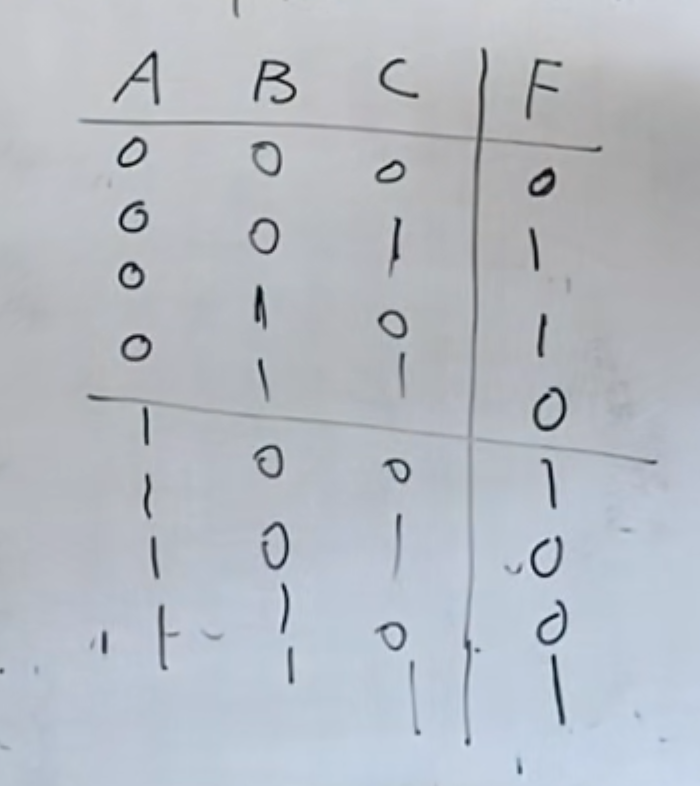
NOTE
本质上是奇偶校验设计
这里如果使用真值表,其实是不能实现化简的。但是使用逻辑表达式化简,根据图上的步骤结果就是

使用数据选择器
首先要明确数据选择器具备哪些输入、控制端。
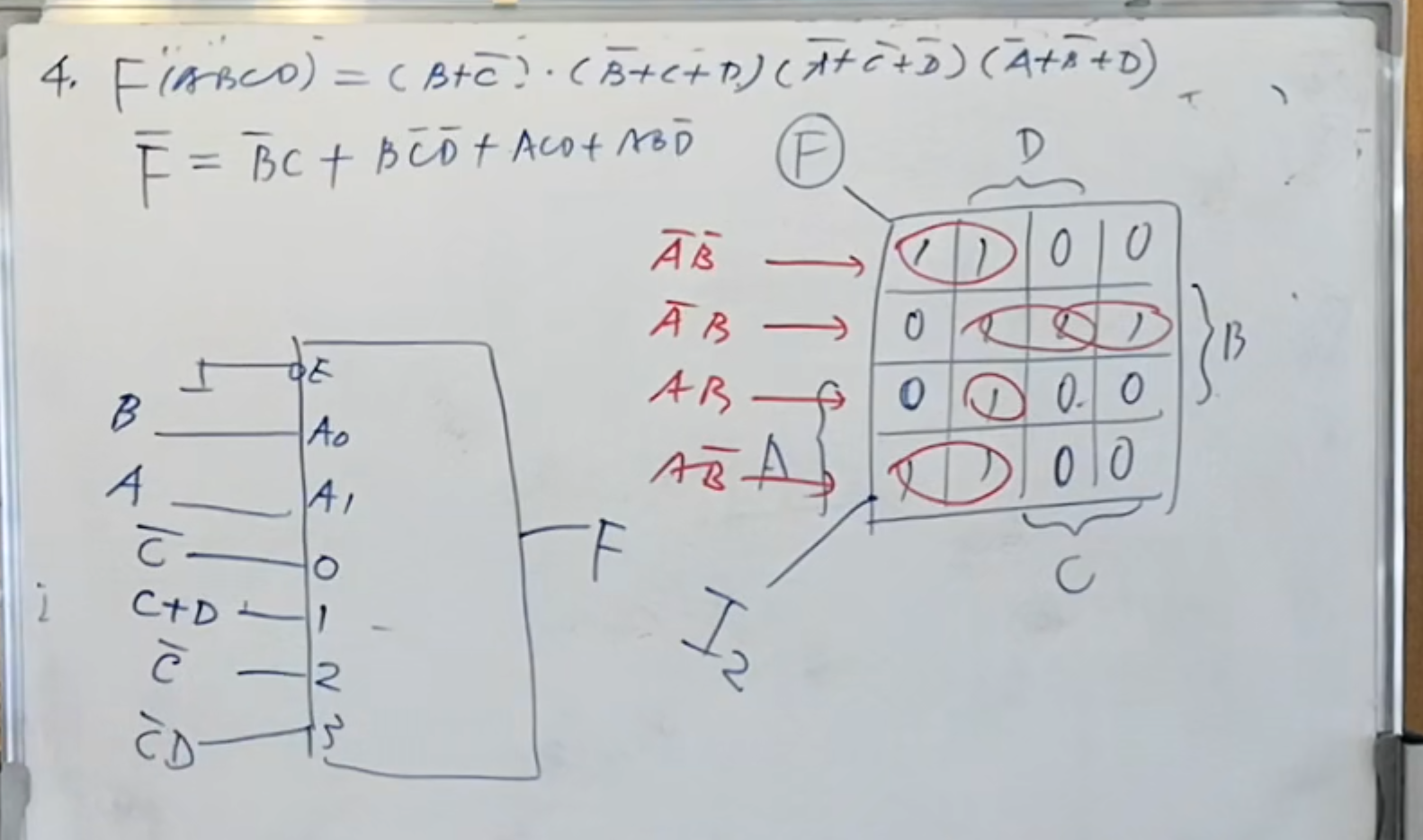
然后,根据提供的逻辑函数、最小项等条件画出卡诺图,如果是上面这种或与式,那么就需要对其化简,或者直接取反。
下面是第五题:
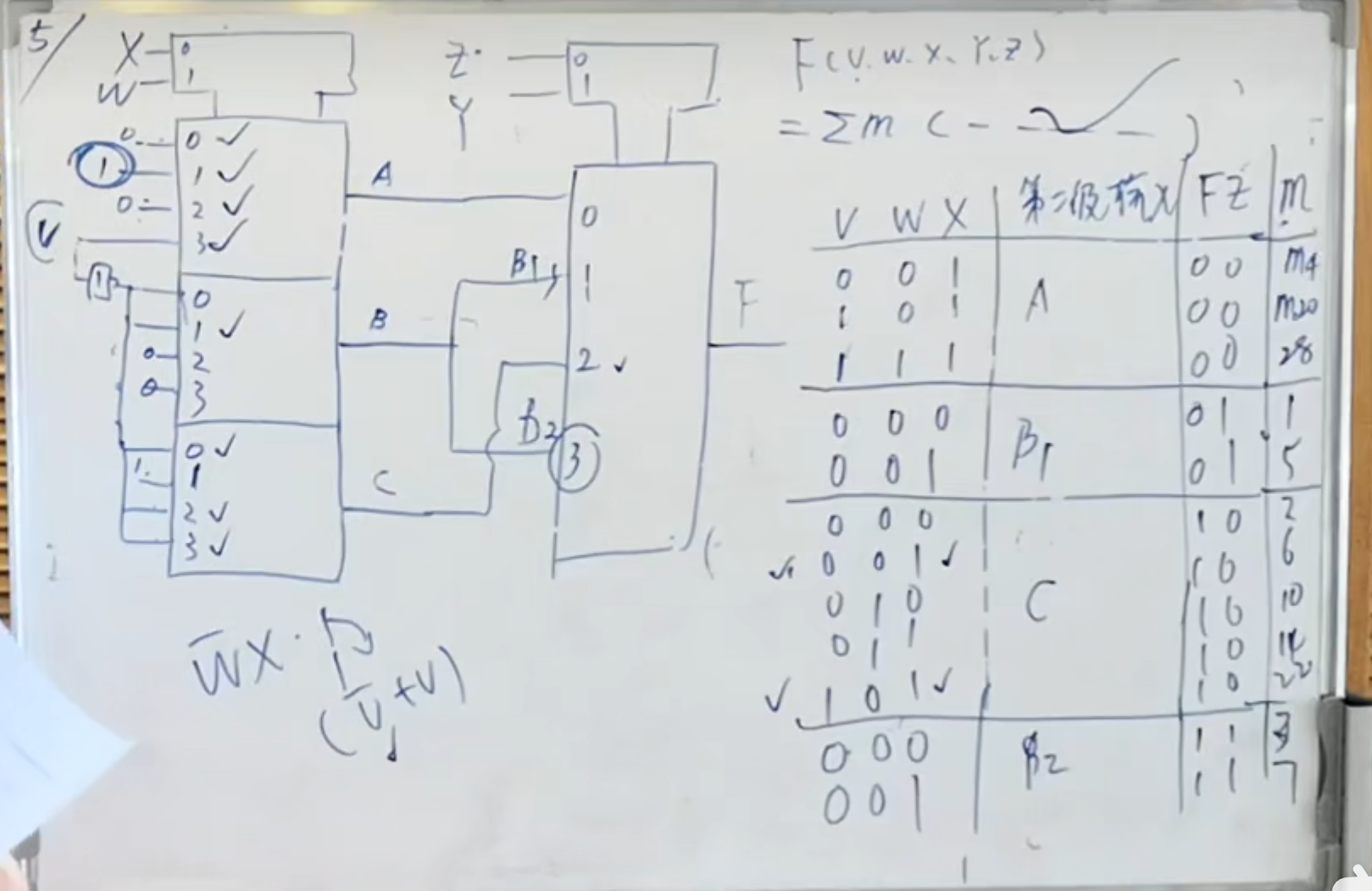
这个题比较复杂,原因在于是一个五变量的函数,对于卡诺图来说,最多只学过 4 变量的卡诺图。
勘误:上面图中右边的表,上面表头部分应该是
我们可以使用画表的方法来实现对此函数的分析。
首先是第一级的输入,关键在于是对
以
然后是对于
然后是
最后是
其他的部分亦是如此,按照以此类推的方法得到每一部分的结果。
然后再结合第二级的输入,也就是第一级的输出。由于这里第二级的输入是作为数据输入端,那么还需要结合第二级的数据选择端。
最后得到的每一行,按照顺序就是最小项的结果。
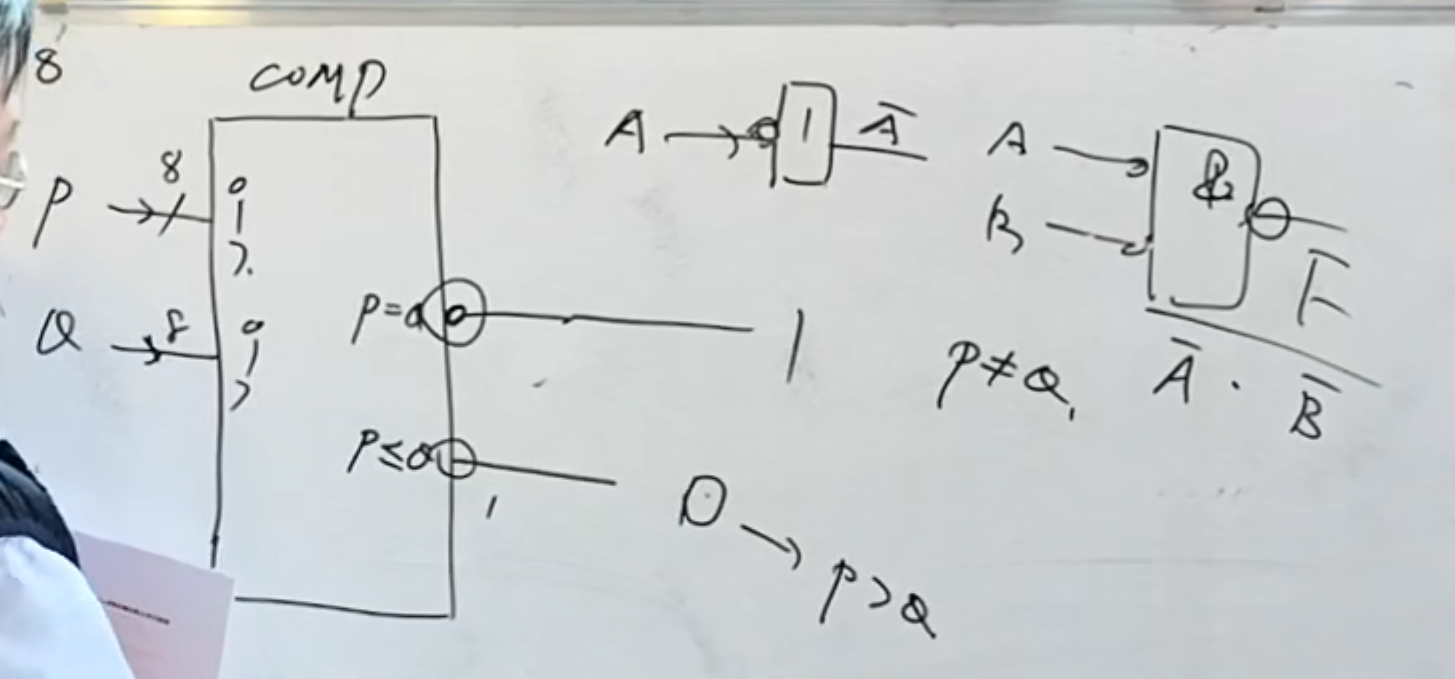
使用数据比较器
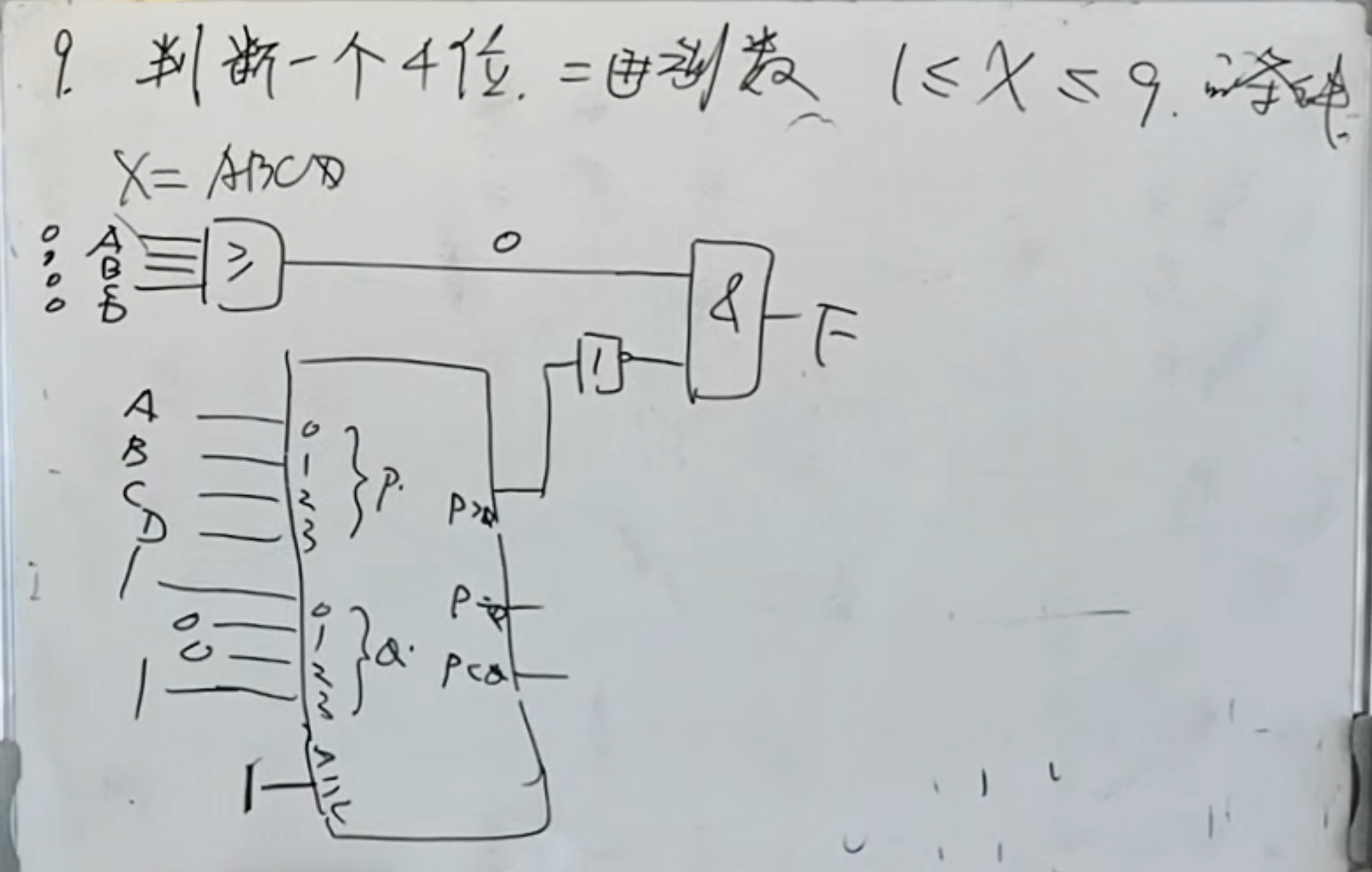
可以使用卡诺图的方法(逻辑电路的方法)来实现:
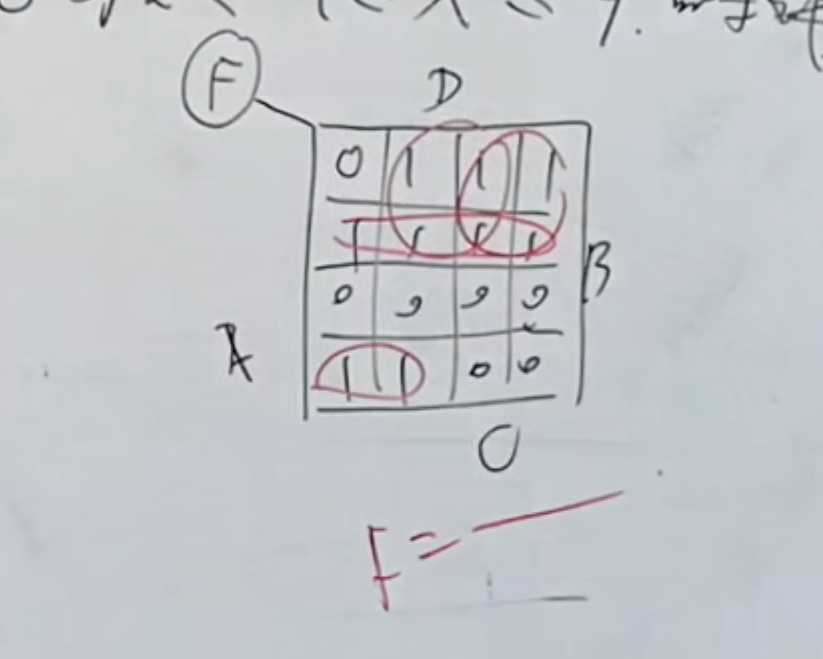
但是如果要使用中规模集成电路--比较器来实现:
那么就需要考虑选择范围。

TIP
勘误:上面图中的
如上图中所示。因为是
根据图中所得,上面或门主要是将
那么就能得到最后的结果。
下面是第十题:
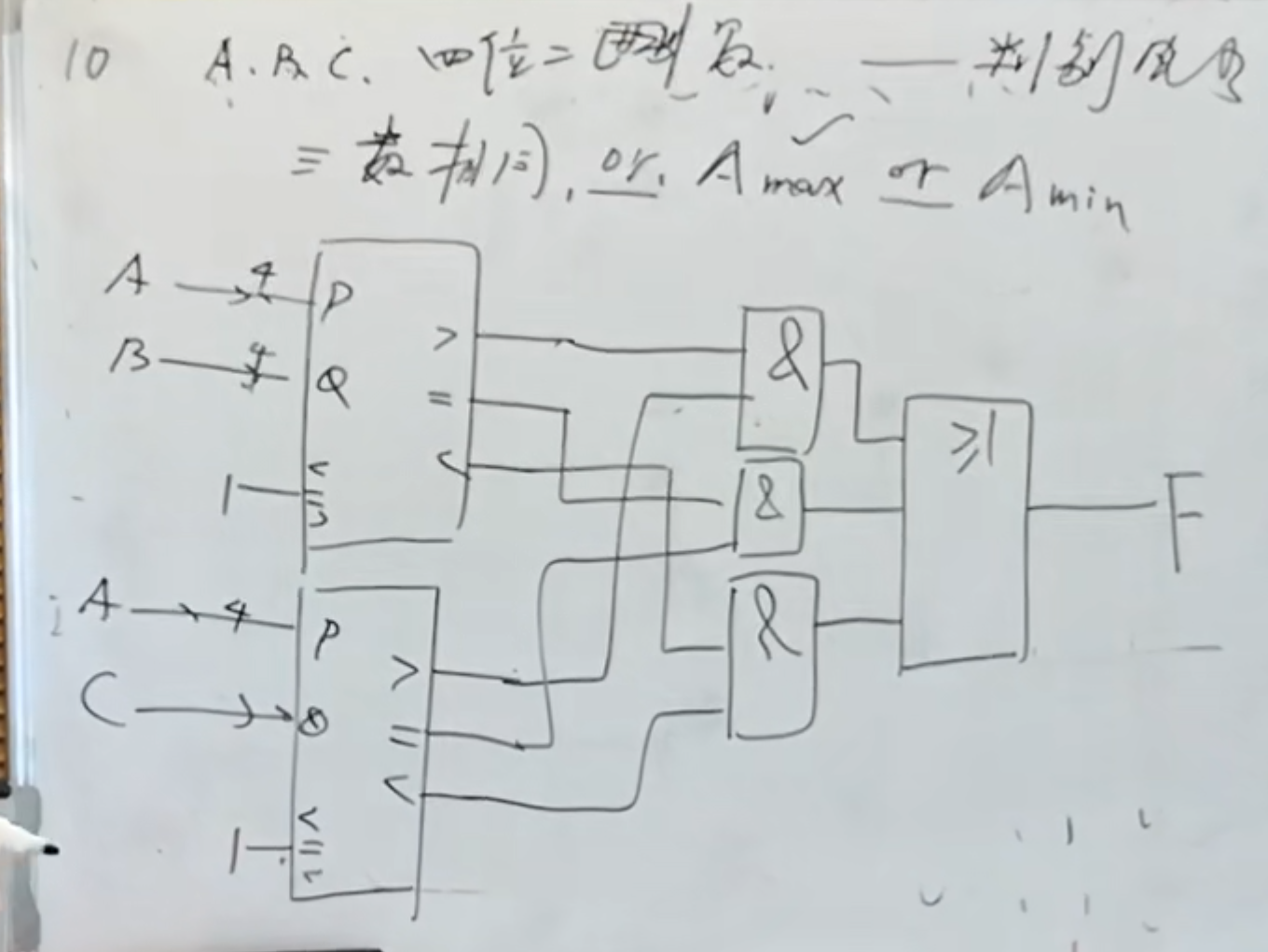
主要核心问题是理清楚逻辑。
此外,要注意观察每个接口处是否存在非,也就是小圆圈,一旦存在,意义相反。
触发器
这个例题是一个同步的,无反馈线的,
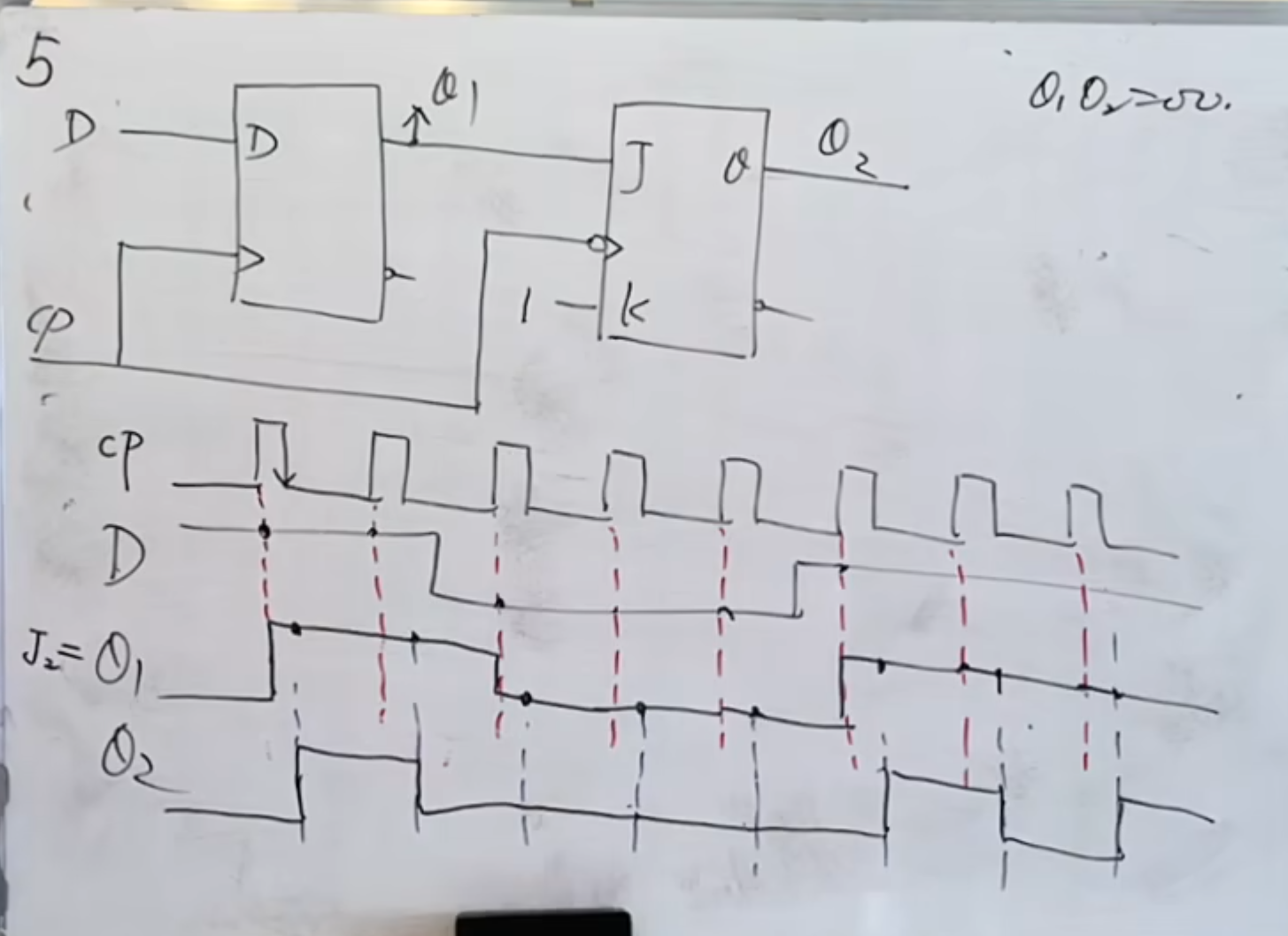
NOTE
只要是相连的,并且没有反馈线,那么做题顺序就是先
如果有反馈线,那么
下面是有反馈线的:
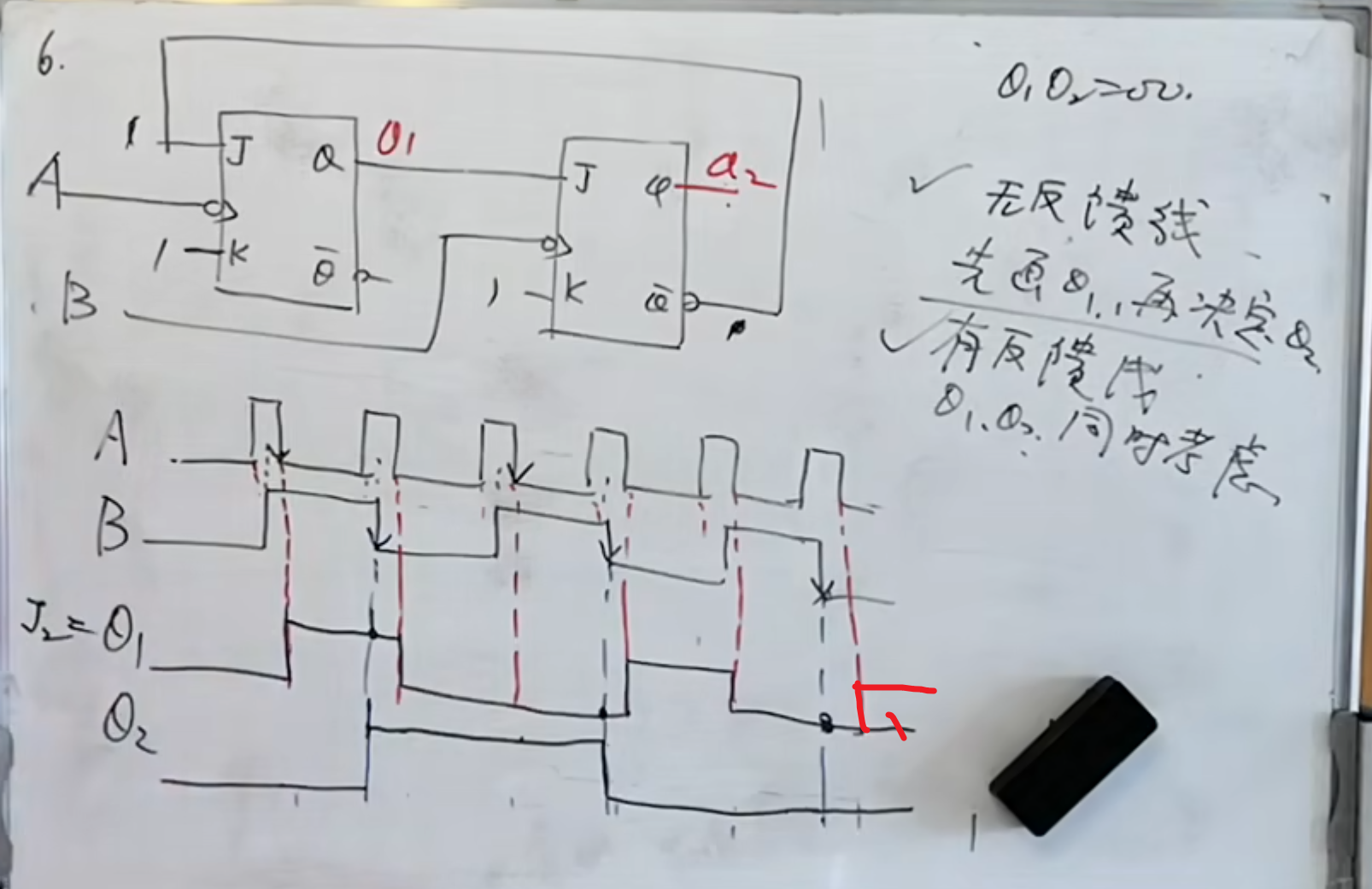
有反馈线的,就要慢慢分析,前后是有联系的,相对来说比较复杂。
再来一个例题:
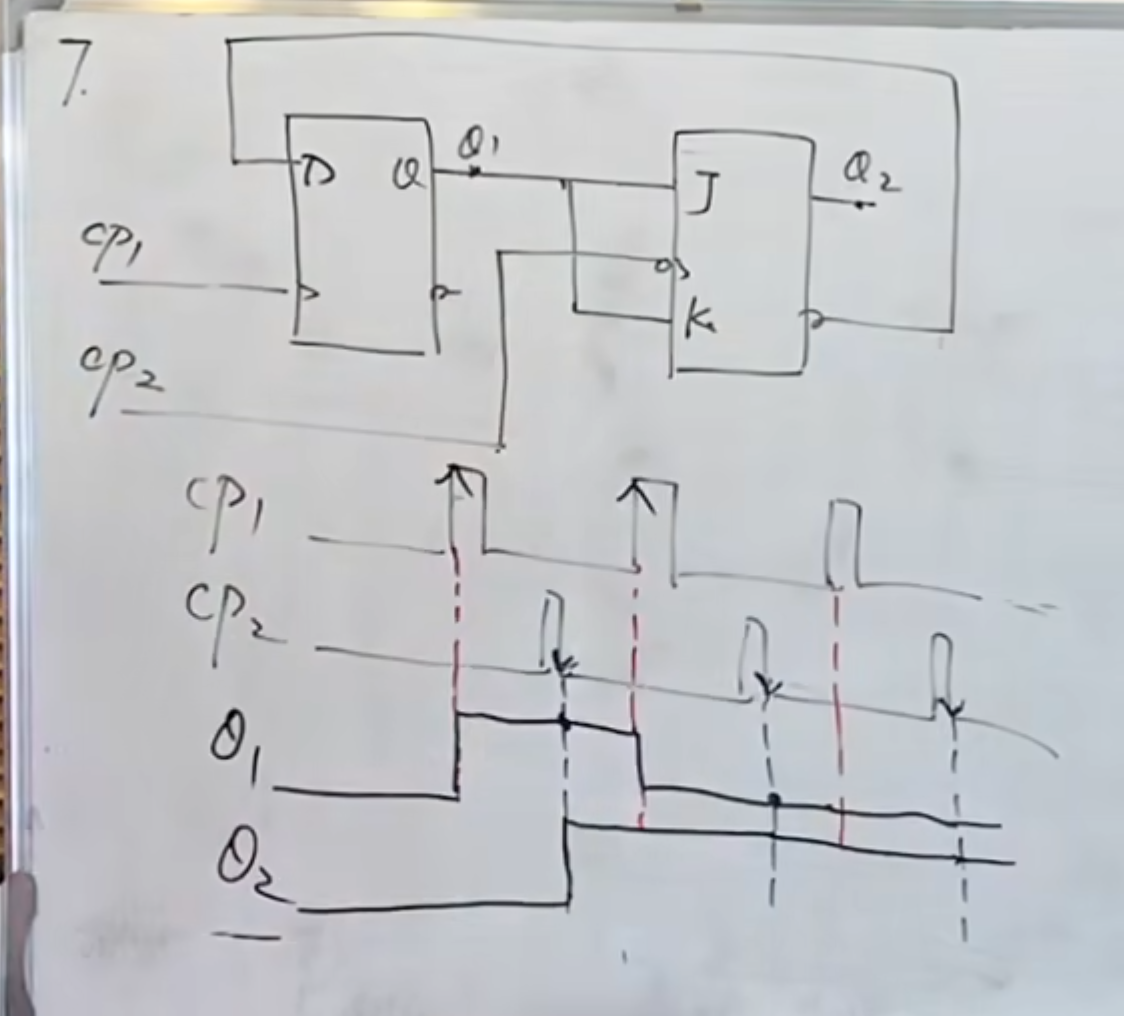
再来一个最复杂的:
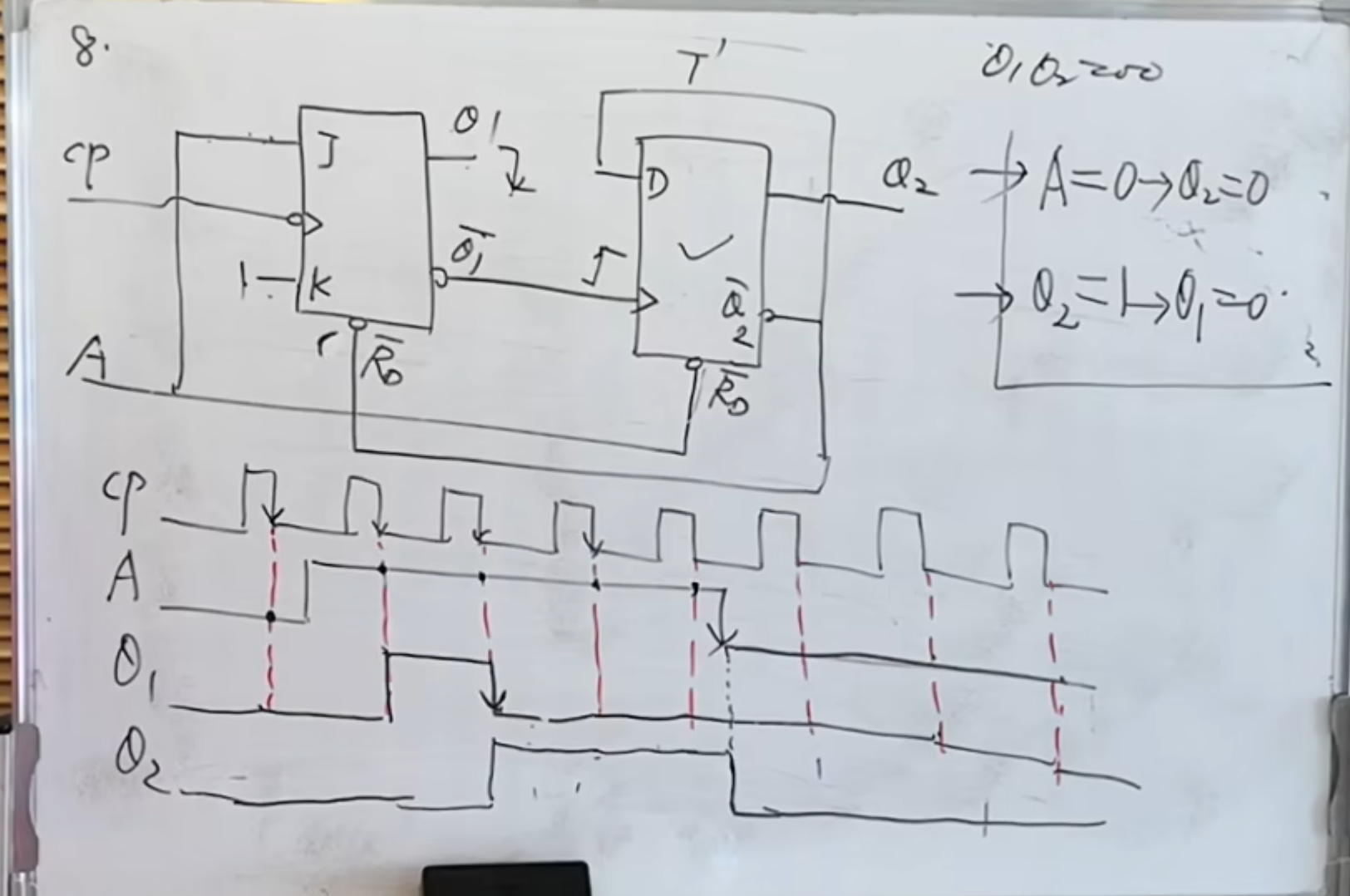
这个要注意的是第二个
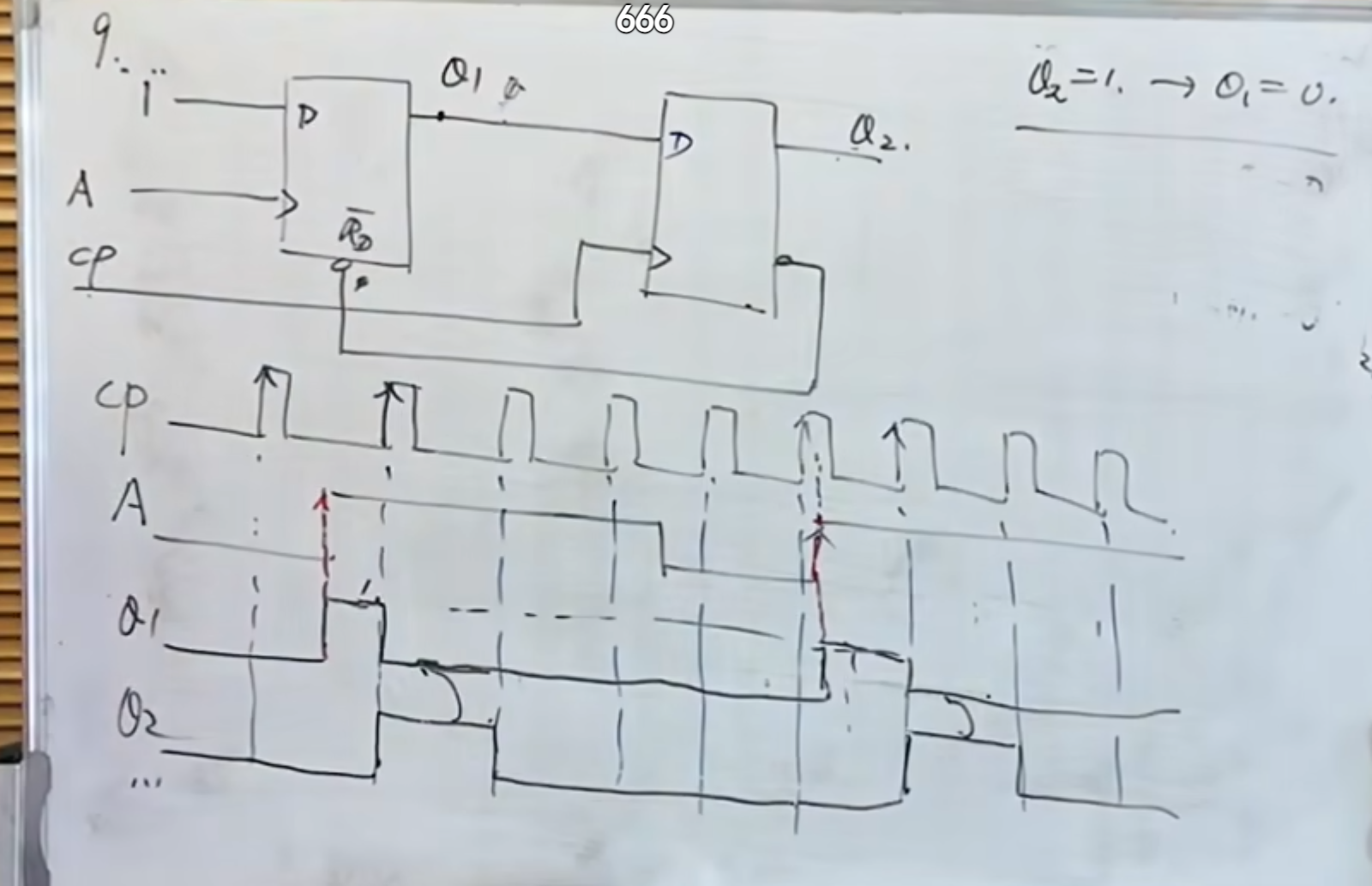
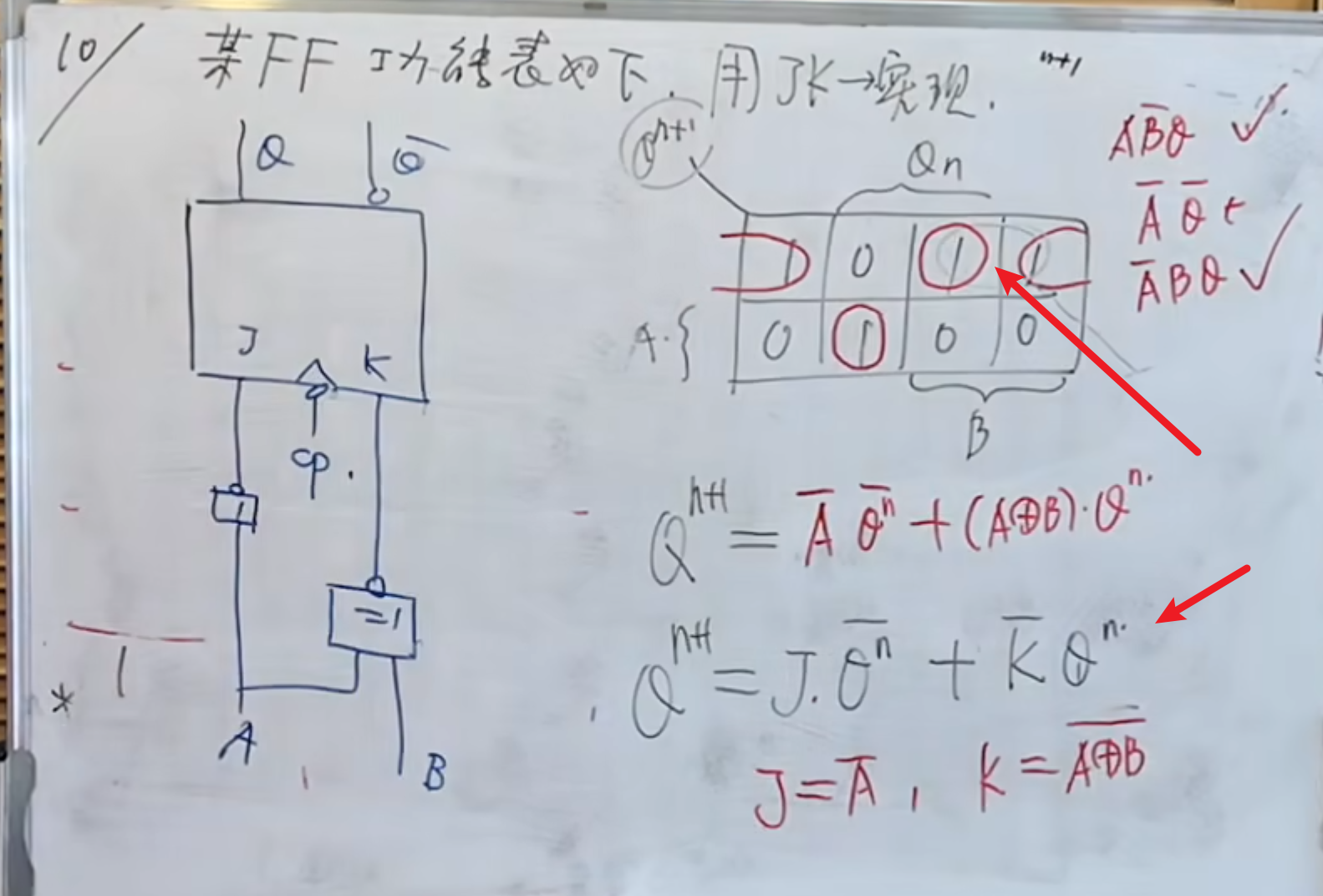
下面这个题则是利用功能表以及

实现方法也不难,主要是将函数表达式表达出来,然后对照
然后将函数表达式换成与
NOTE
注意,在这里有的时候表达式未必要化到最简。
时序逻辑电路
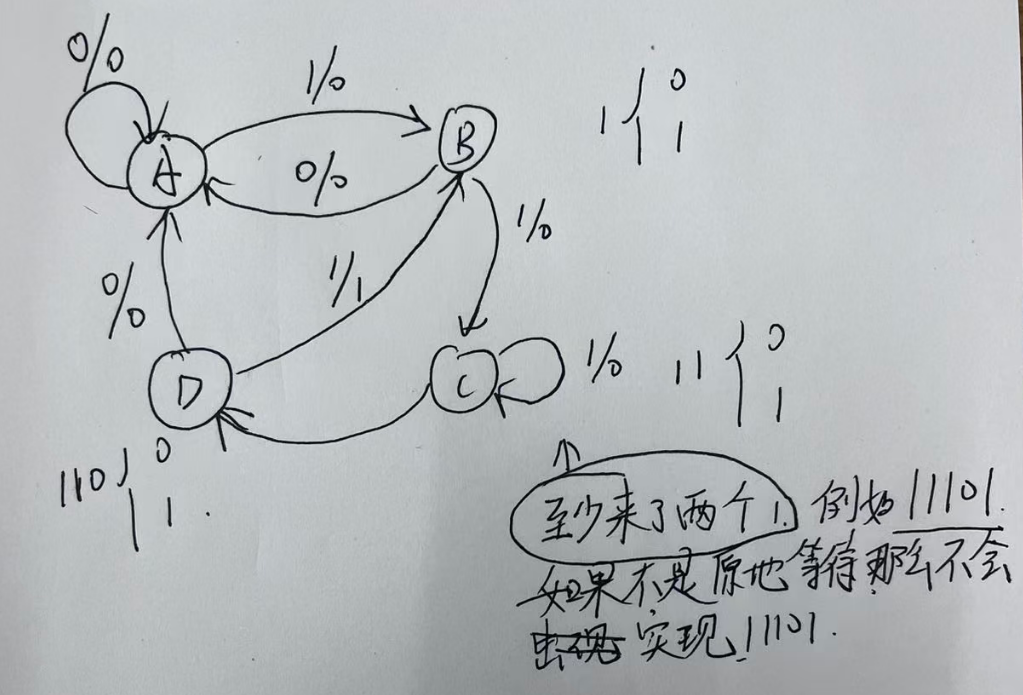
序列检测器的设计
1、使用
(状态分配:
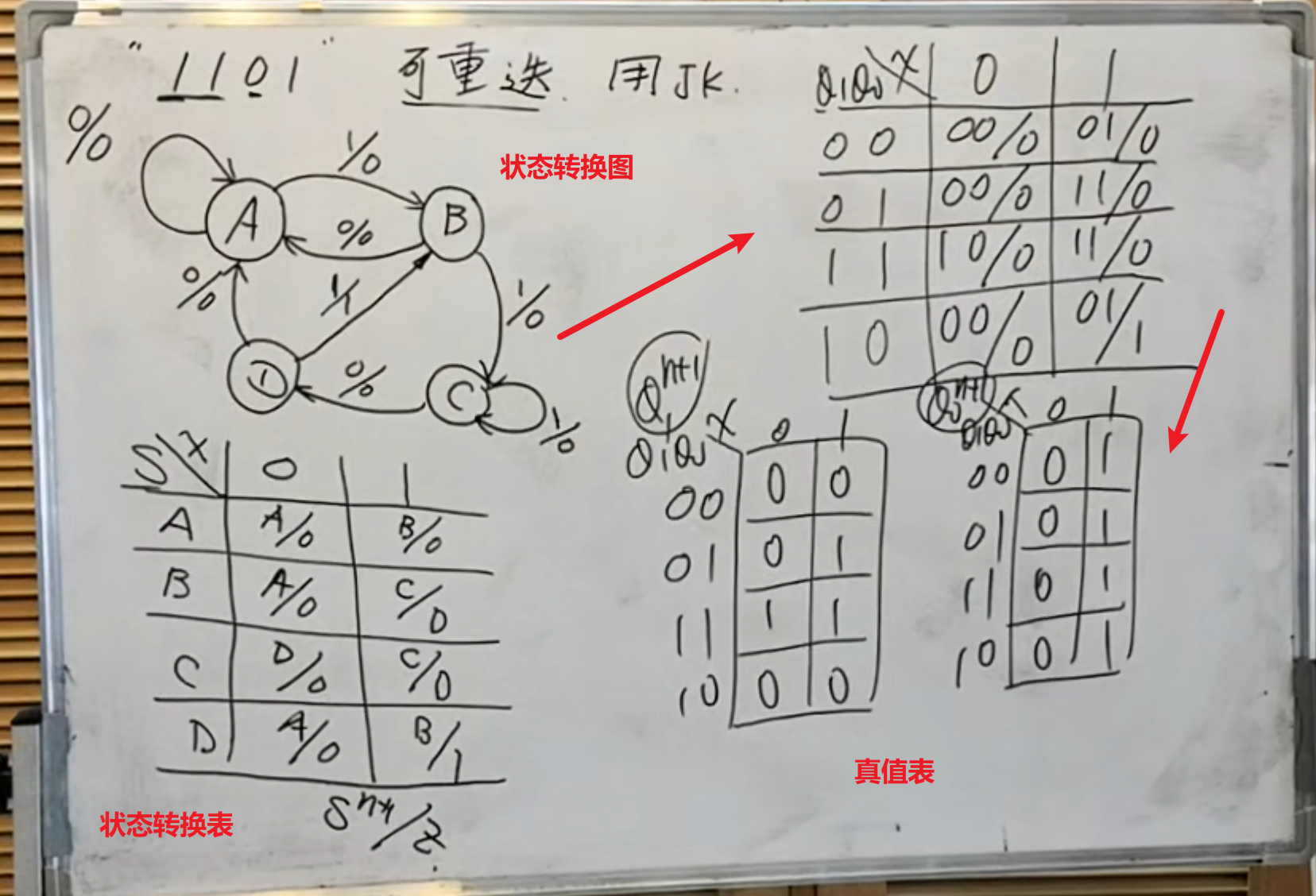
NOTE
注意,在这里已经事先确定好了状态对应关系,所以不需要改动。如果没有规定状态对应关系,需要将其按照真值表的顺序来排序。也就是
然后是根据真值表以及

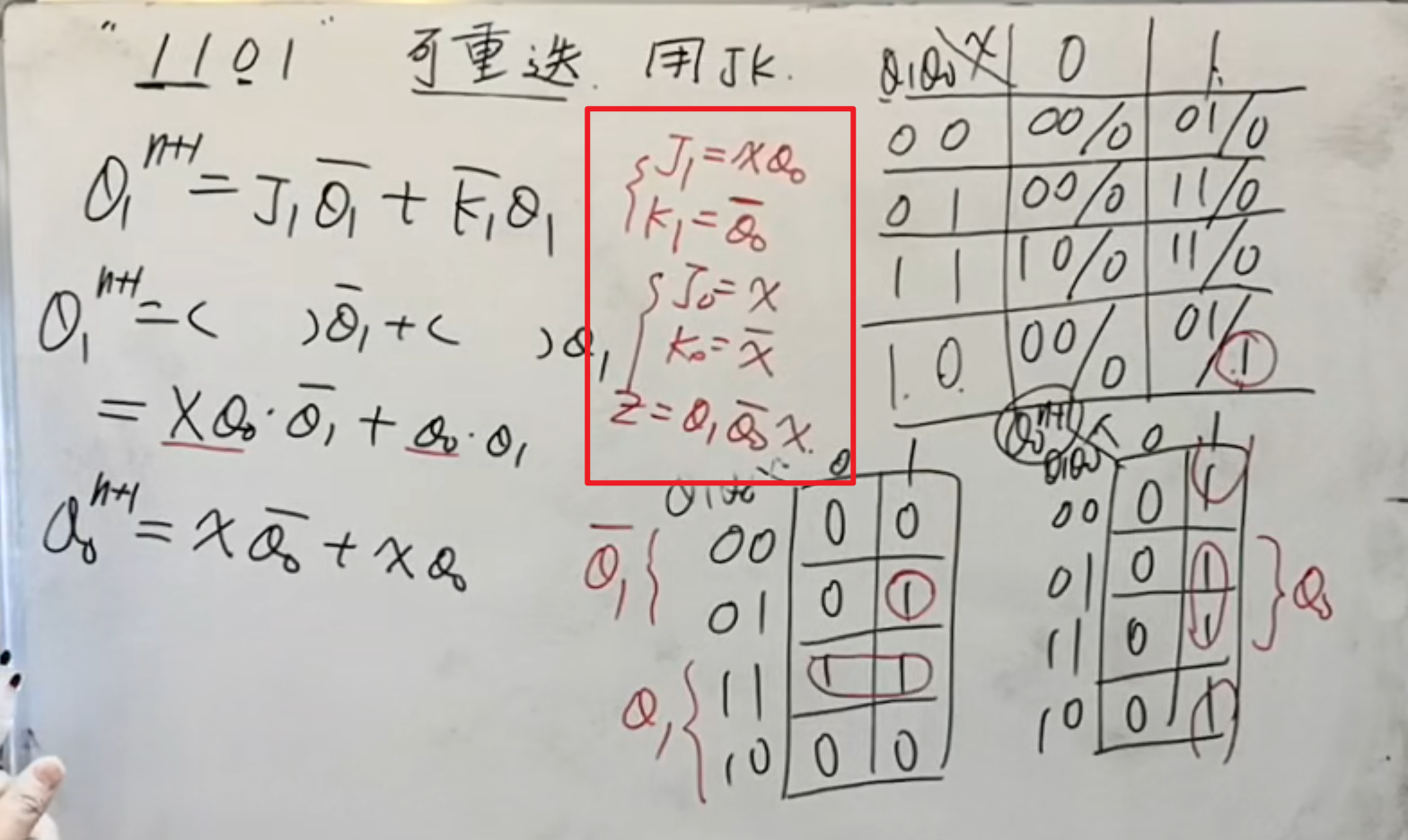
模 5 计数器的设计
使用
开始的时候直接写出状态转换真值表
NOTE
注意,过程中会有三个状态是不再循环中的,所以他们的输出设为
然是,将真值表画出来。当然在画圈化简但是依然要结合
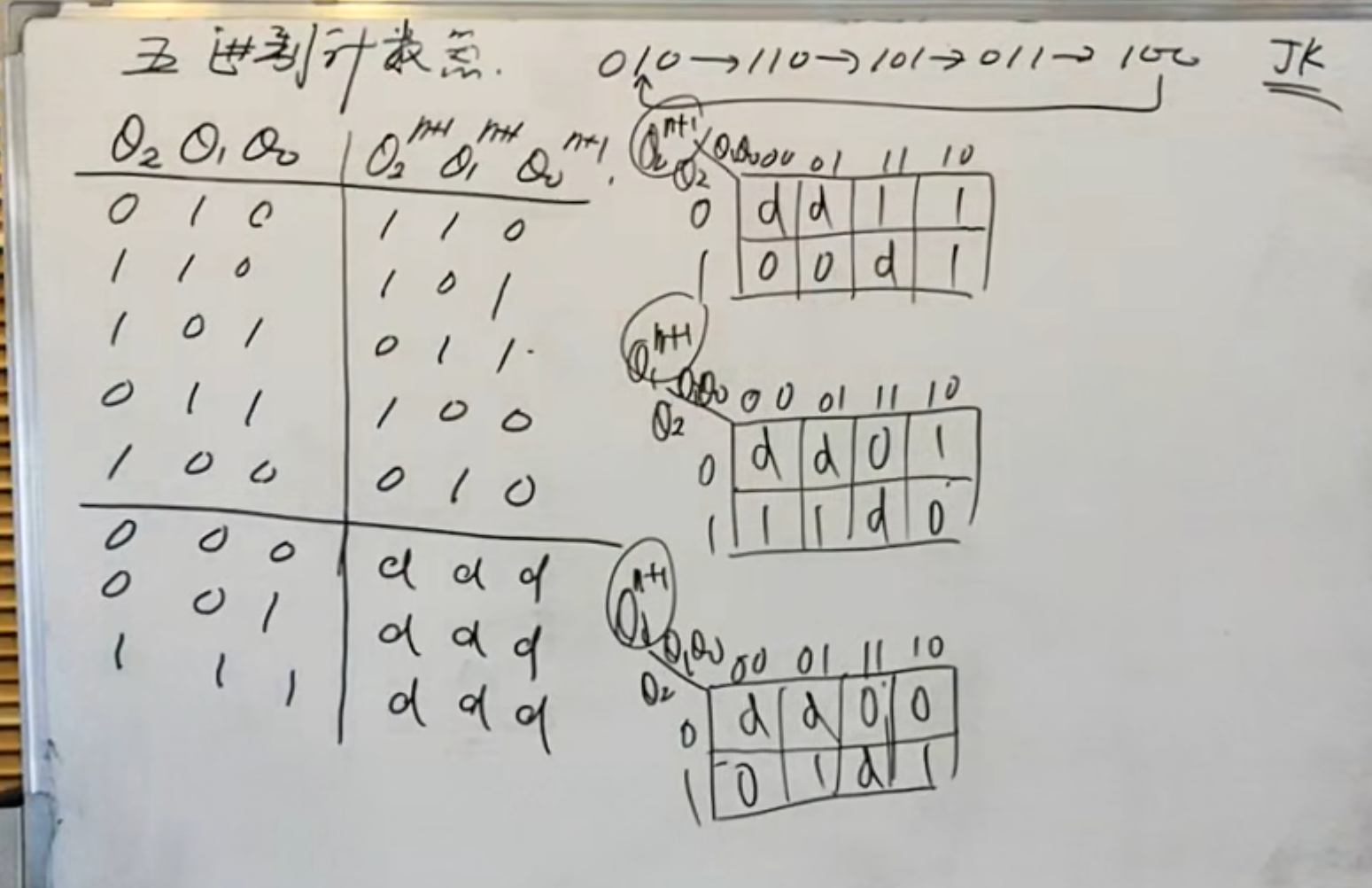

分析得到状态方程之后,还没完,还要讨论对于不在循环下是否会出现挂起的情况。
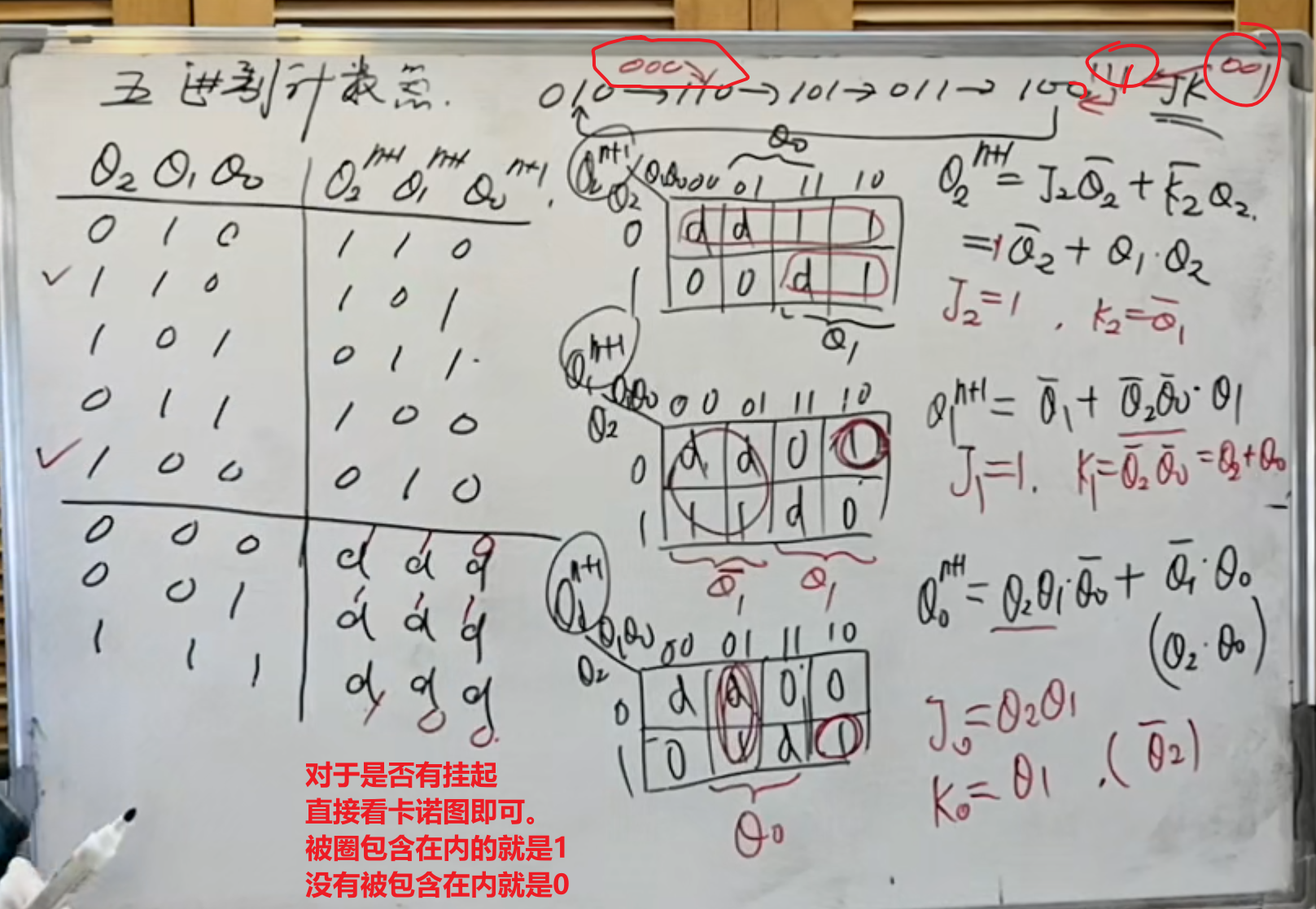
如果对与此类问题要求有输出,姑且当作
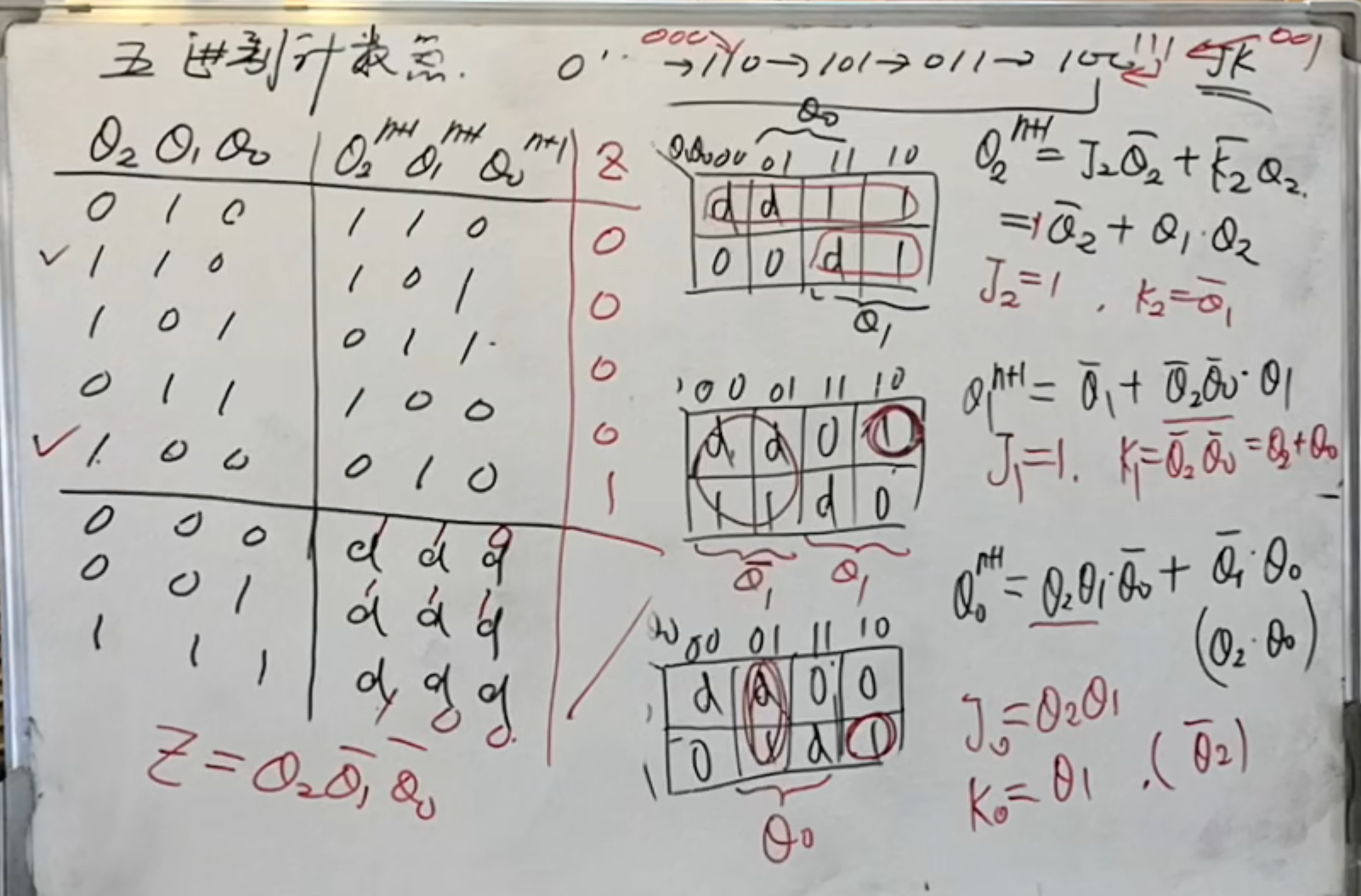
一般来说会规定在哪一位上输出
根据已知序列检测器的状态转换图设计电路

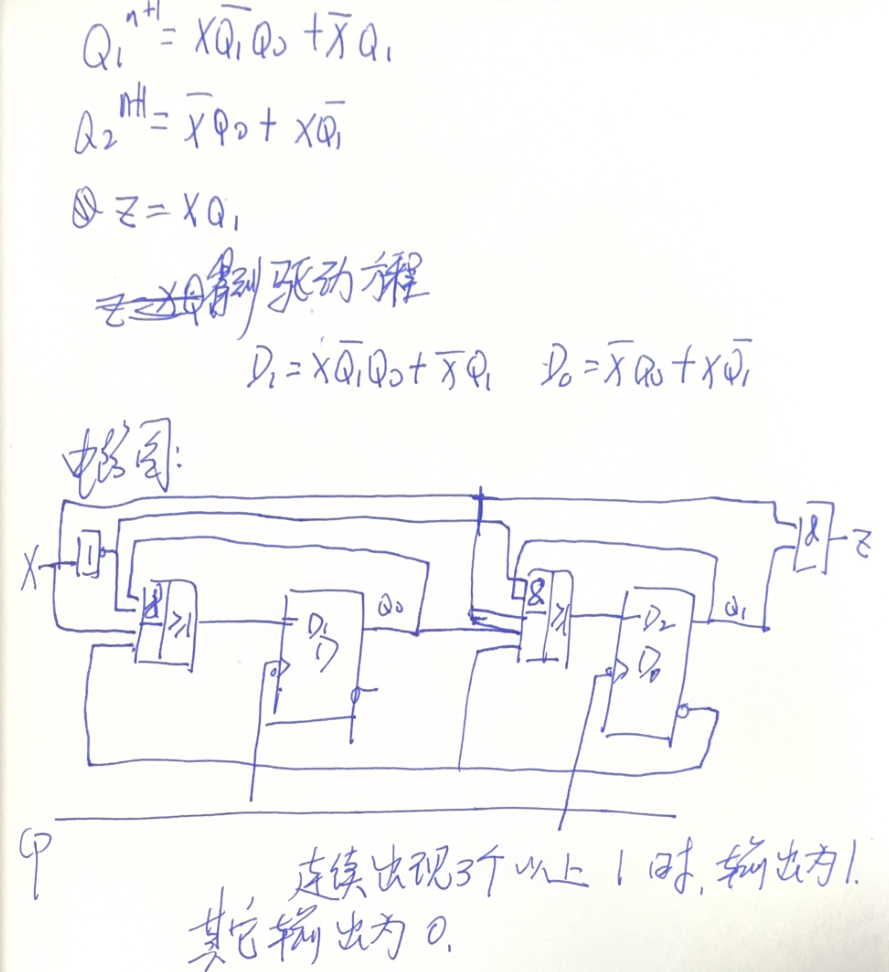
单稳态触发器
第一个题目是求

其中,
而
NOTE
稳态肯定是
如果稳态是
当来一个上升沿触发之后,会导致
如果没有阈值,那么
而在有非门的影响下,
计算
可以得到:
第二个题目:
这个题目也是求出

已经给定是负脉冲触发。
只需要逐步分析即可。

第三个题是:
设计一个可延迟触发的双脉冲产生电路

这道题目比较难,难点在于在原来基础上还要加上一个
 王海平
王海平