引言与例题分析
在时序逻辑电路中,应当都具备有下面三个方程:
从大的角度来说,时序逻辑电路分成:同步时序逻辑电路和异步时序逻辑电路
同步,意味着多个触发器的
异步,相对比较复杂,除了考虑状态变换之外还需要考虑

下面来分析一个时序逻辑电路:
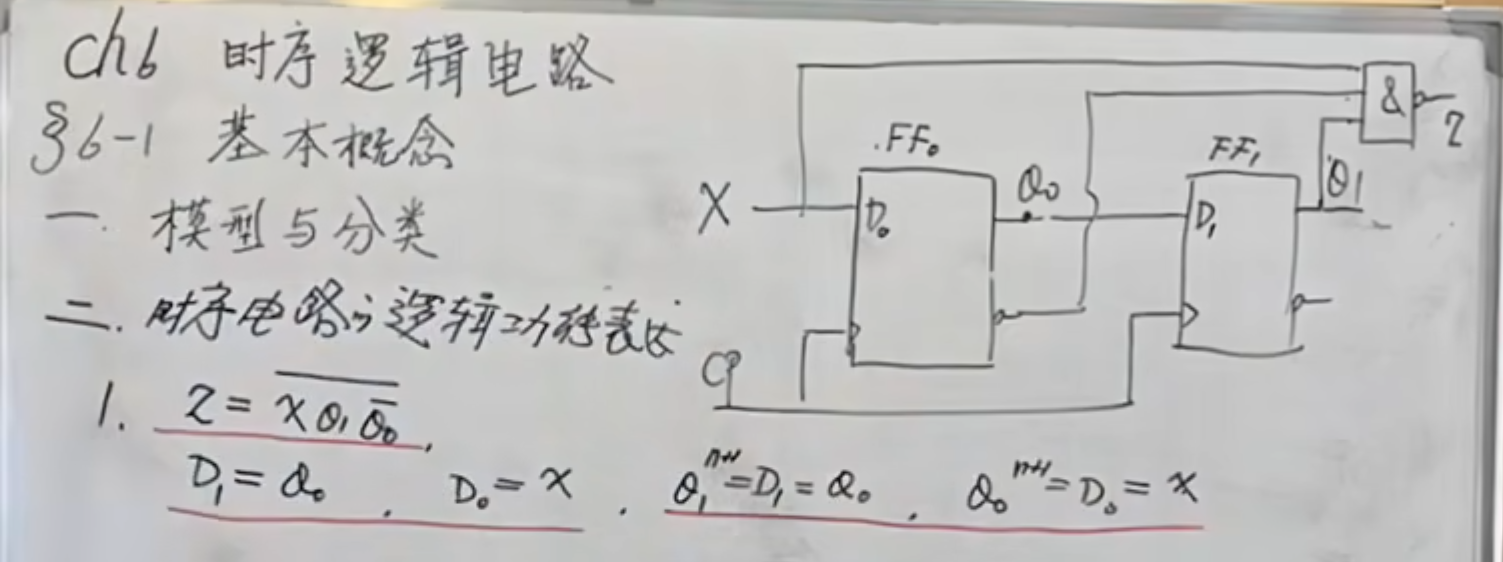
上图中列出来的方程就是全部的方程。
下面根据方程,画出真值表:

而状态表或者是状态图也都是根据真值表得到的:
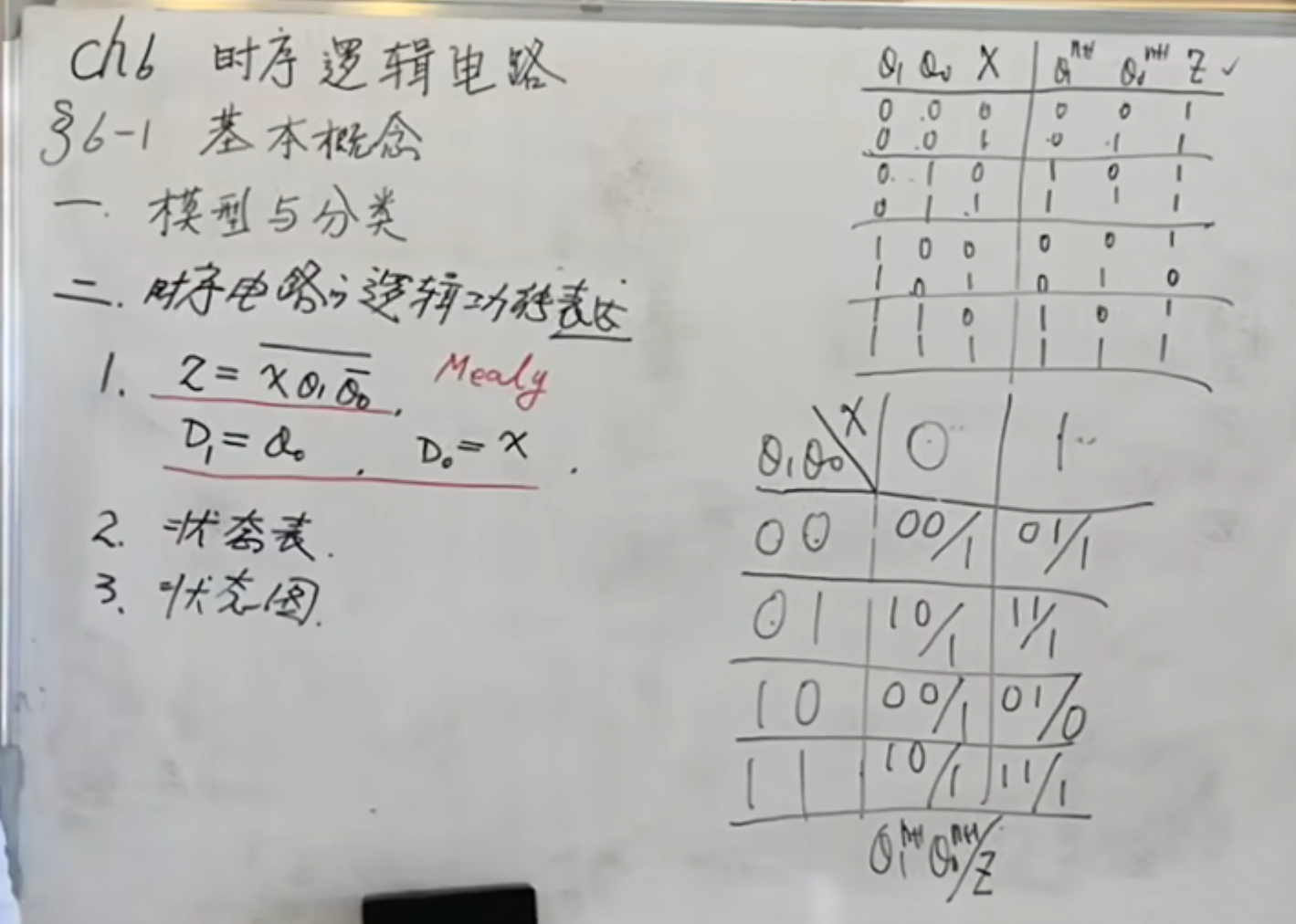
状态表要注意的是,里面的内容代表的是下一时刻的状态,下划线是对应的输出是什么。
换句话说,就是现在的状态由输入和前一时刻的状态决定。现在状态的输出同理。
状态图:
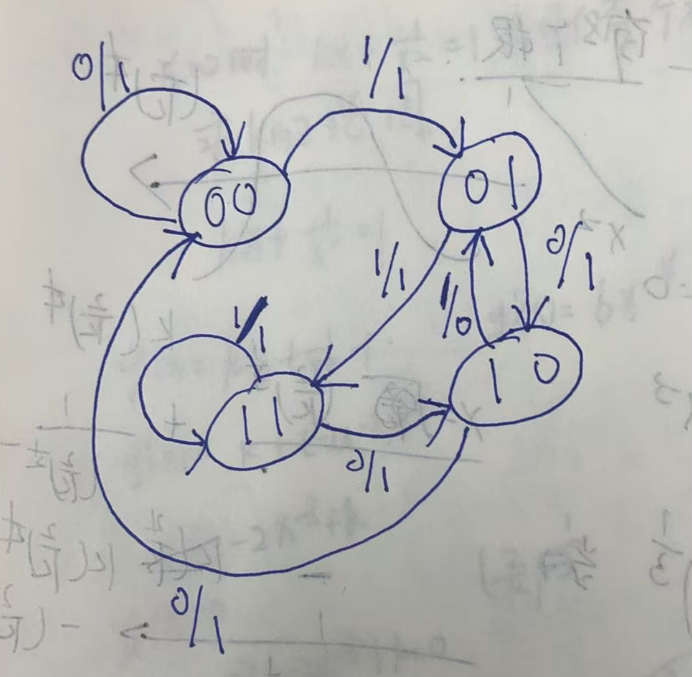
对于状态图,无论是对照真值表还是状态表,都是可以得到的。
NOTE
圆圈内代表的是状态。箭头则是代表从当前的状态变化到下一个状态,在变化的过程中,斜线上面的代表的是输入,而斜线下面的代表的是输出。
时序图:
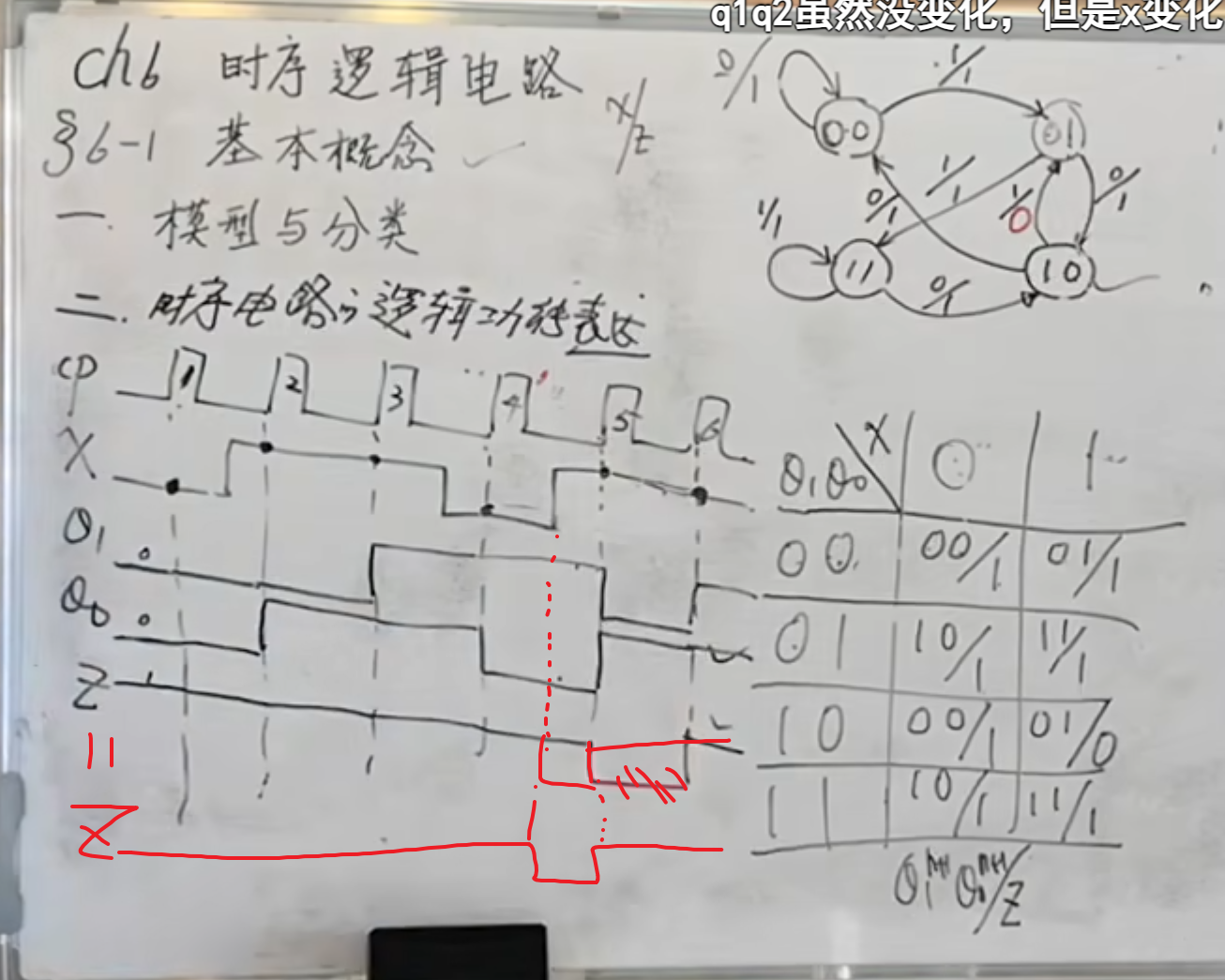
IMPORTANT
这里需要注意的是,
原因在于这里的输出是将输入与两个输出与到一起的,并不属于时序的范围内。
时序逻辑电路的分析
同步时序逻辑电路的分析
一般步骤与例题
时序电路的分析是从图得到其功能如何。
NOTE
一般步骤:
列方程组(3 个)
列状态表(功能表),画状态图
功能的说明(该电路的逻辑功能)
下面以一个例子来分析:

首先是将每一步的方程都写出来,包括每一个层级的输出。
写出方程之后,根据方程表达式画出真值表。
再根据真值表,将状态表画出:
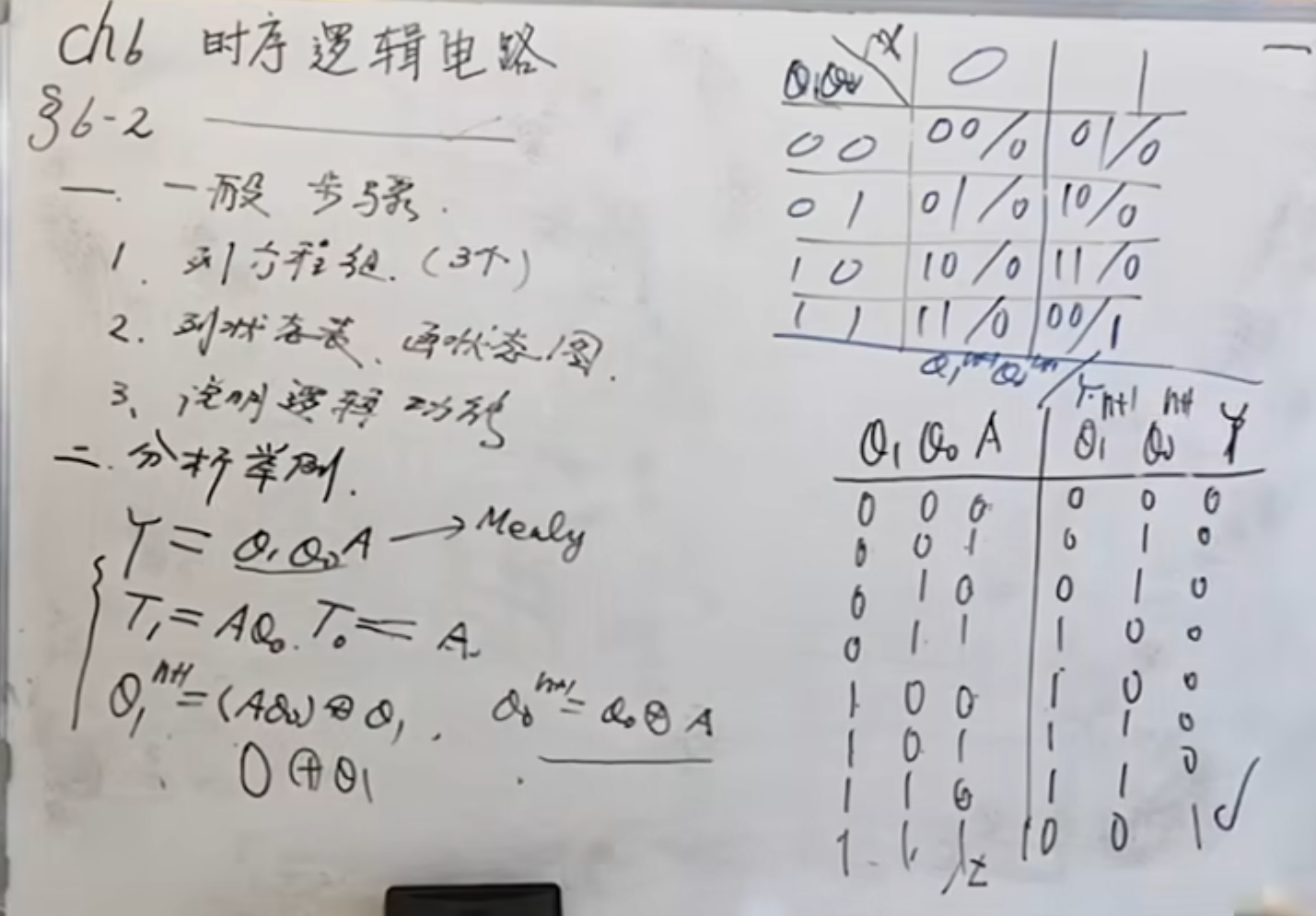
最后根据状态表将状态图画出来。
NOTE
对于一个状态来讲,有几个输入无所谓,但只能有两个输出

如果需要的话,还可以画一下时序图:
对于任意的输入
根据状态表、状态图可以得到时序图:
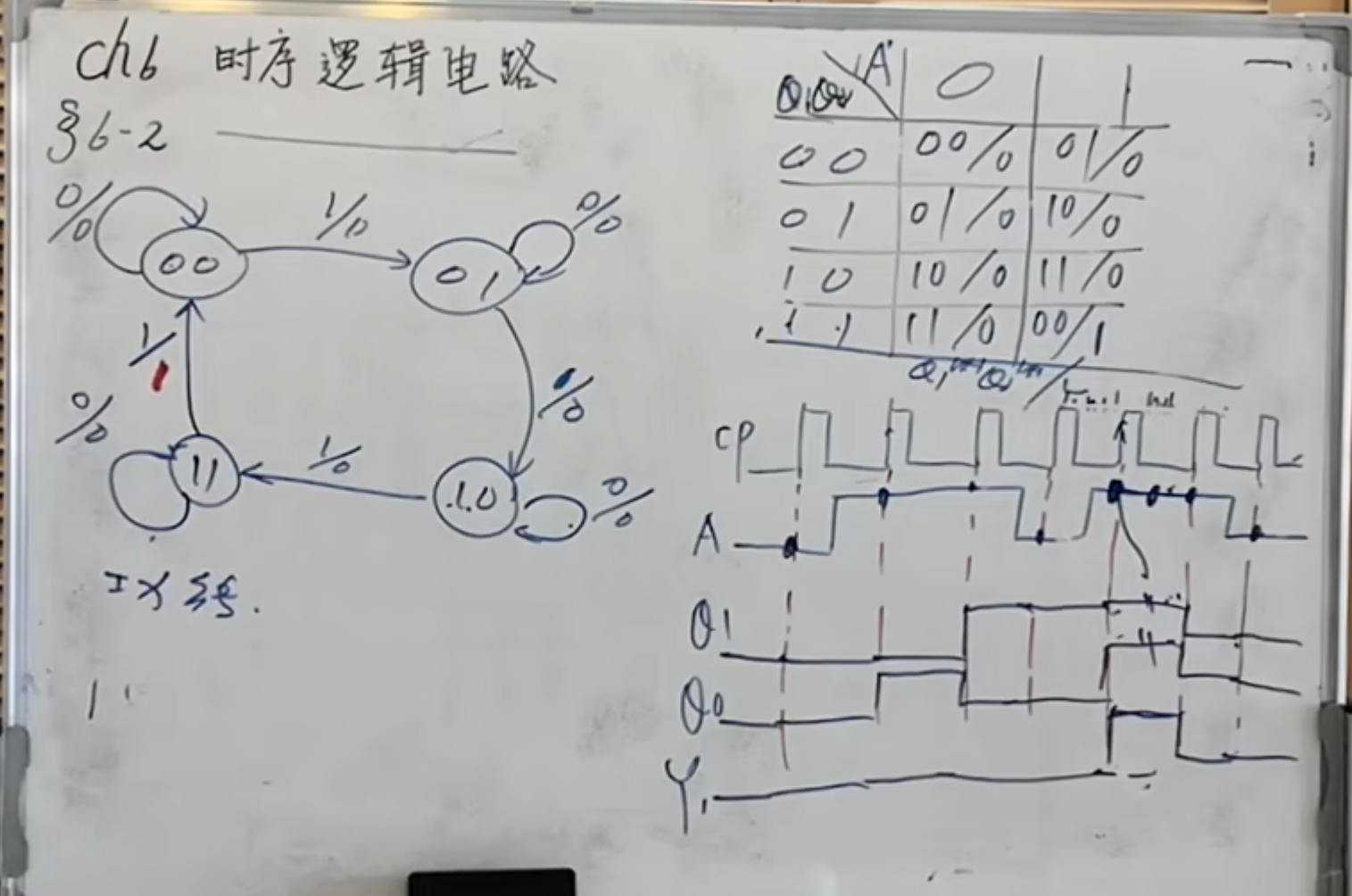
最后,就是说明这个实现的功能是什么
只要讲得通,找到它的规律就可以。可以通过观察状态图:
当输入为
当输出为
再来一个例子:
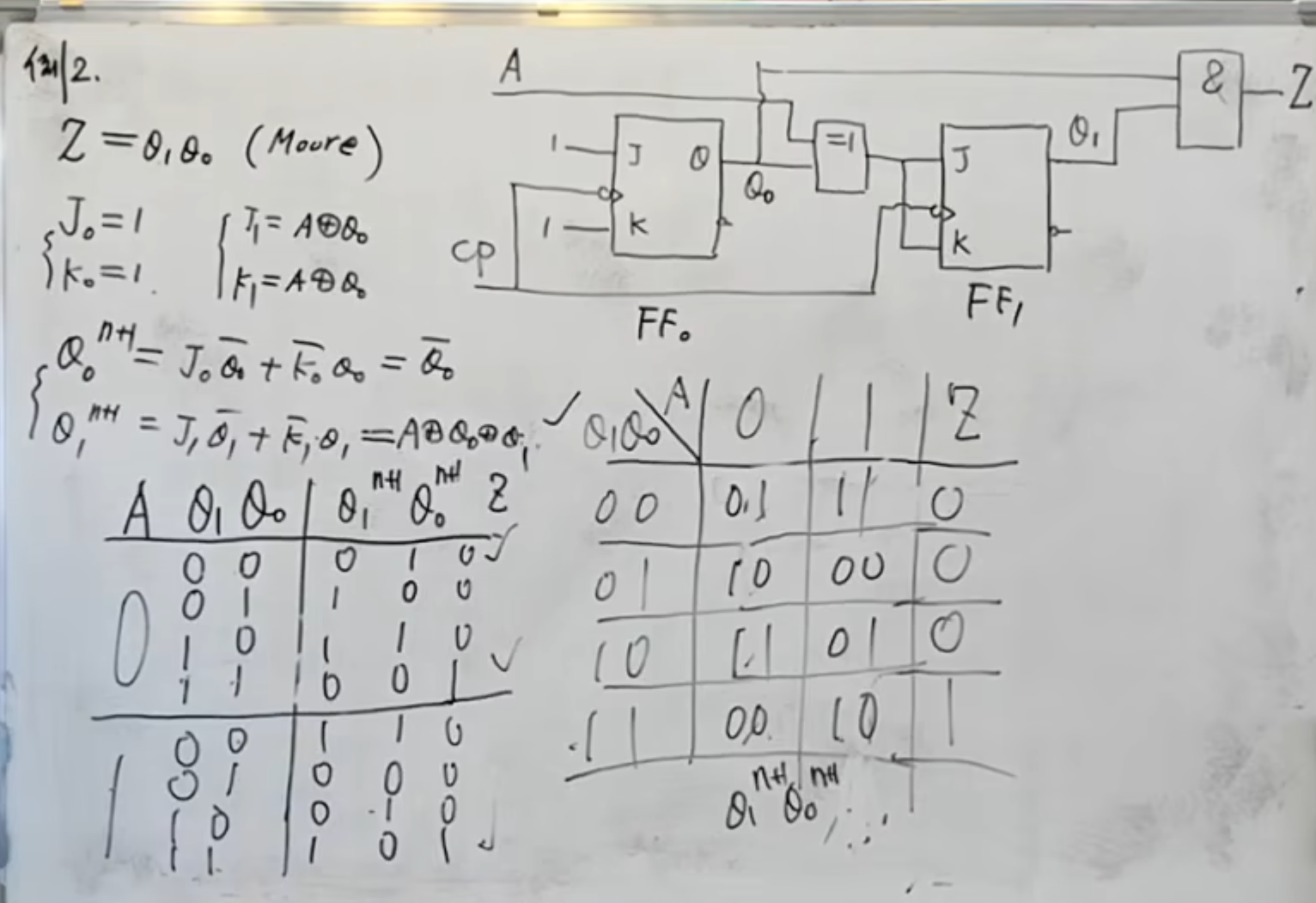
思路是一样的,依然是先写出特征方程。
然后根据特征方程将真值表画出来。
再根据真值表将状态表画出来。
NOTE
由于这个输出与状态转换(不严谨,理解意思即可)没有关系,所以在画状态表的时候,习惯上将输出
最后是将状态图画出来。
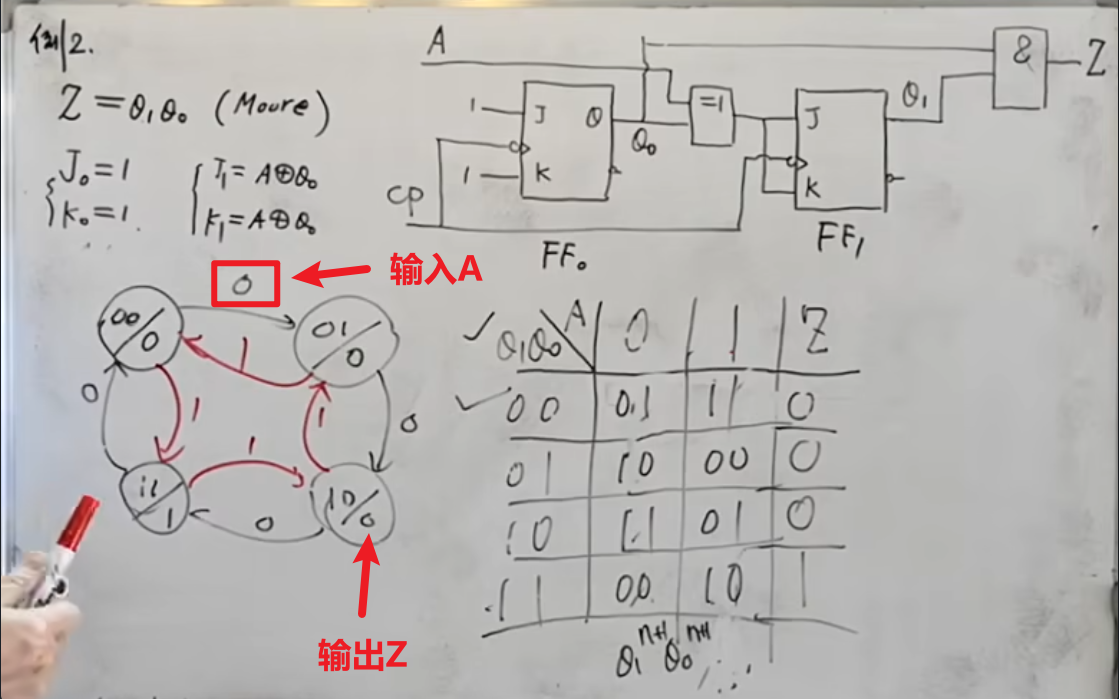
在画状态图的时候,依然是因为输出只与连个触发器的状态有关,与转换没有直接关联。
所以可以直接在每个状态下面写上输出是什么。
最后如果有需要可以再写出时序图。
NOTE
最后说明它的功能:受
用触发器实现计数器
IMPORTANT
状态转换真值表对于同步的电路分析来说比较好,如果是异步的,不是很合适
用一个例题来说明:
首先在思路上,是与之前的几乎一样。

先将方程写出来,包括输入和输出方程。
然后是写出真值表。(注意,这里没有输入,完全是由
就可以发现,它是从
而对于剩下的三个状态,因为输入的时候是有可能处于剩下的三个状态中,如果这三个状态可以恢复到五进制的循环当中,那么就称之为无挂起,反之,如果有某个状态的下一个状态还是它自己,那么就导致了挂起状态。
上面这个就叫做无挂起同步五进制计数器
下面再用一个例题来说明更简单的计算方法。
当然首先要做的还是写出输入方程等特征方程。

在写出特征方程之后,就要进行分析。
而在这里,就不再用之前的那种分析方法了,而是用:状态转换真值表
这个表的关键在于其中包括前一时刻的输入,直接按照 BCD 码的形式写下来即可。
然后是每个触发器的输入,分别是
最后面是要计算得到的
其中的
NOTE
注意,在这里默认
而接下来的分析,则是直接画出状态转换图:
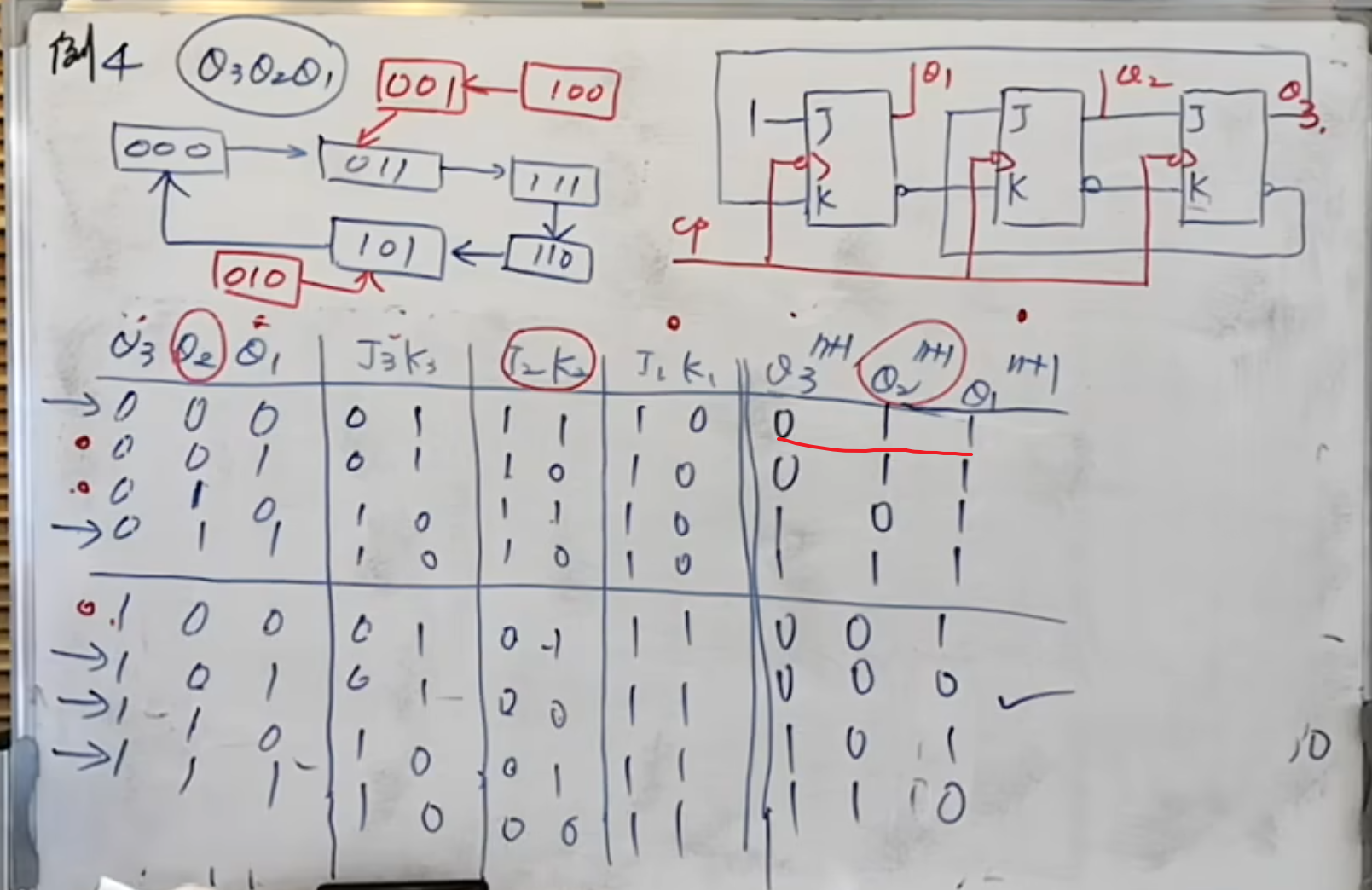
进而得到功能
如果再加一个输出,也是没问题的:
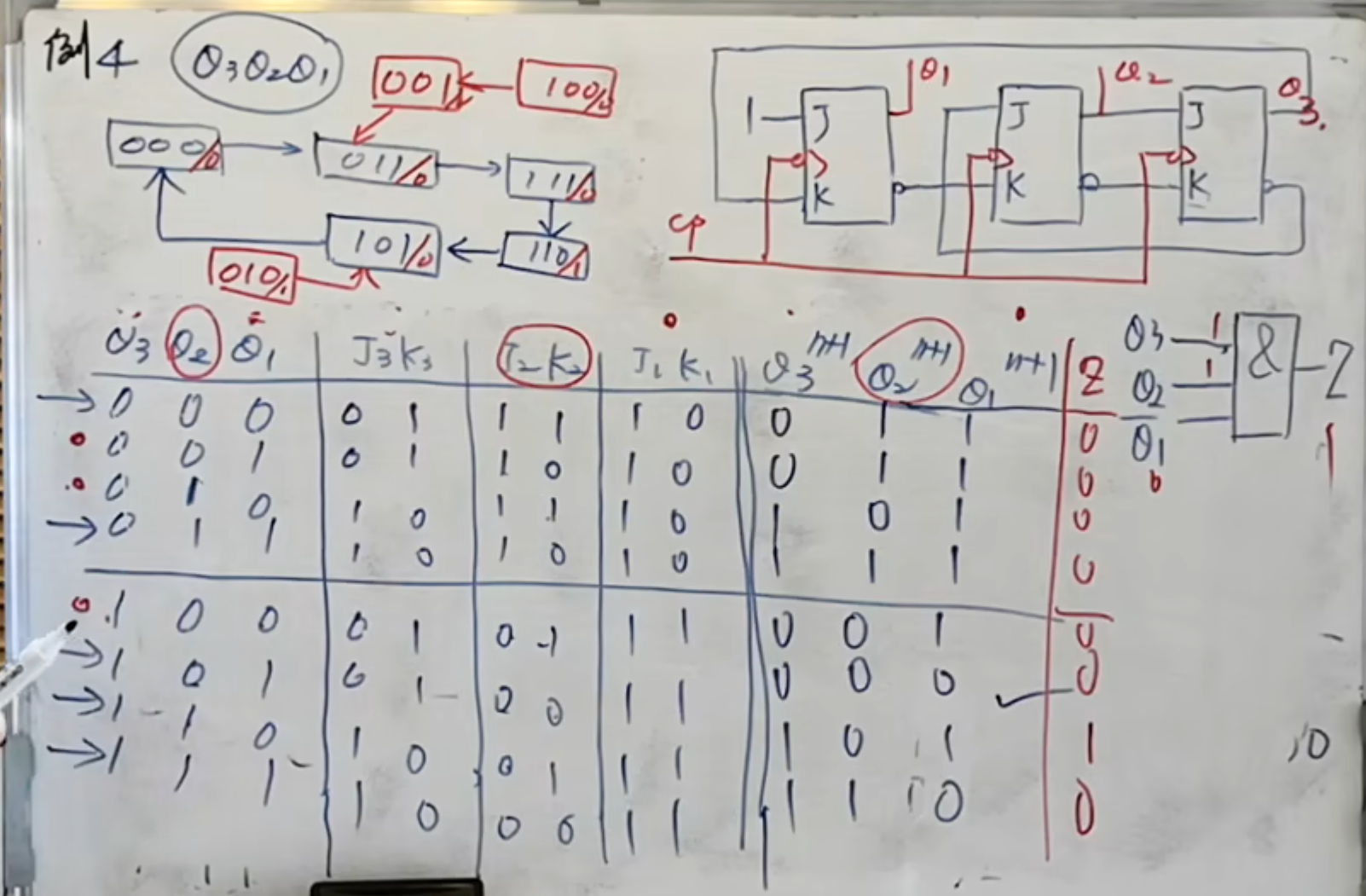
NOTE
当出现挂起状态的时候。
解决方法有两个,一个是置初始值。
另外一个则是使用修正电路(后面会讲的)
异步时序逻辑电路的分析
NOTE
步时序逻辑电路的分析一般来说不能使用同步中使用的状态转换真值表。
但是也不是绝对的,我们需要考虑是否有反馈,一般来说,如果没有反馈,那么是可以逐步分析触发器。
当异步的部分,没有反馈线到前面的部分,那么可以将前面那部分当作同步的来分析,最后再来分析异步的部分。
依然是用例子来说明:
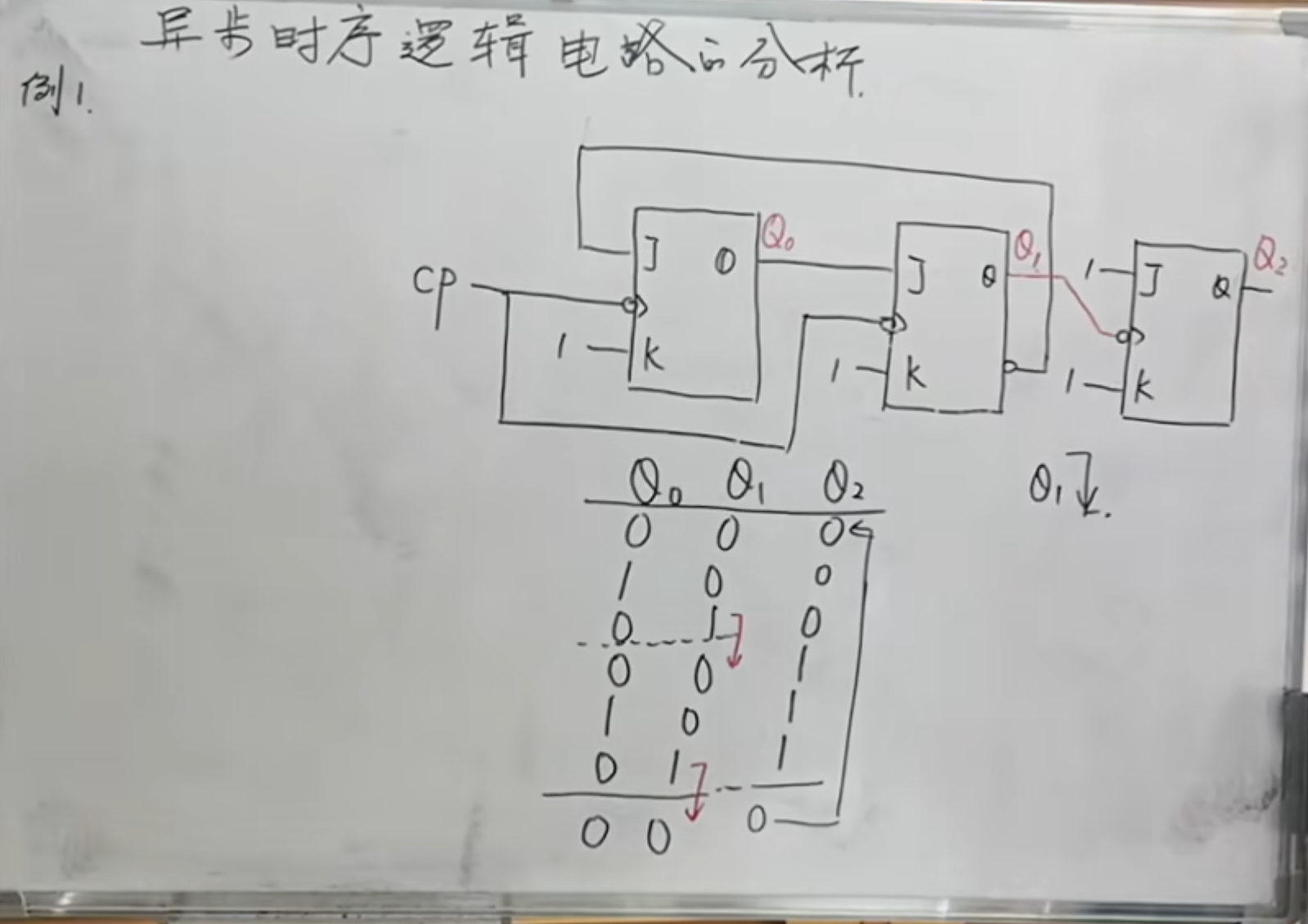
在这个电路中,前面两个触发器就组成了一个同步电路,最后面的哪个触发器才会结合成异步。而这个异步的并没有反馈给前面的触发器,这样就可以分两部分来分析。
NOTE
个人感觉不如使用脉冲线的方法来分析来的直观,这样直接分析比较容易出错。
对于
下面画状态图:

注意,在分析完循环的状态之后,还需要分析以下没有出现的状态的情况,会不会回到循环里面。
综上所述,可以得到上面这个是一个无挂起异步六进制计数器
再来一个例子说明:

这里的关键点在于
下面画出状态图:

同步时序逻辑电路的设计
理论上说,只要是能描述出来的问题都可以用时序逻辑电路来实现。
一般步骤
一般步骤:
- 根据一般问题描述,得到原始的状态图(状态表)重中之重
- 状态化简(等效的,合二为一)
- 状态分配
- 选触发器(
、 ) - 确定激励方程组和输出方程组 (求解
、 等) - 画图以及确定能否自启动(如果挂起如何修复)
序列检测器
序列检测器要实现的是对于输入进来的一组序列,当出现要检测到的
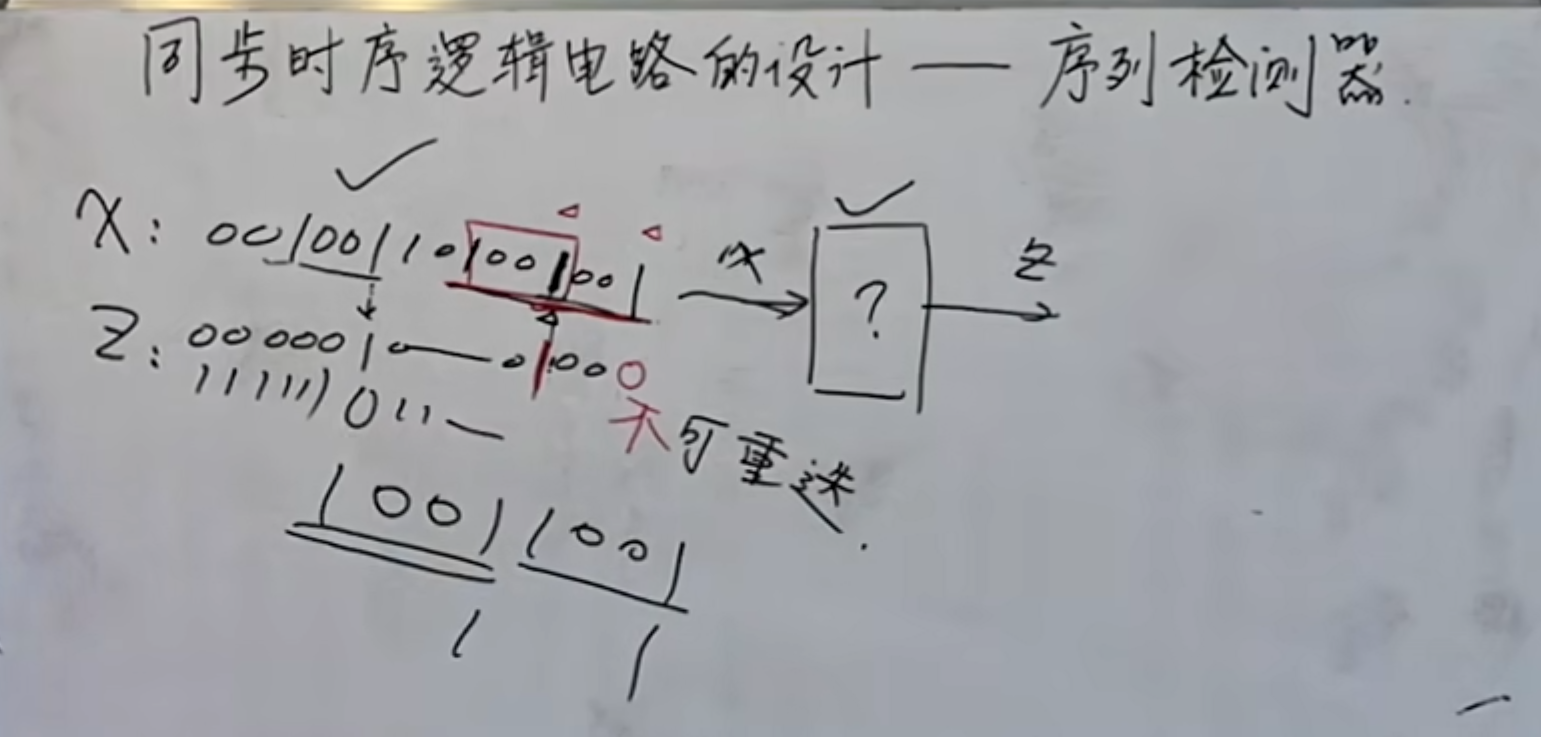
下面用一个例子来说明:
设计一个检测
对于这种序列检测电路,针对一开始的初始状态,一般设置为要检测序列的第一位元素的相反状态。

注意,对于每一个现有状态来说,存在两种情况,一种是输入为

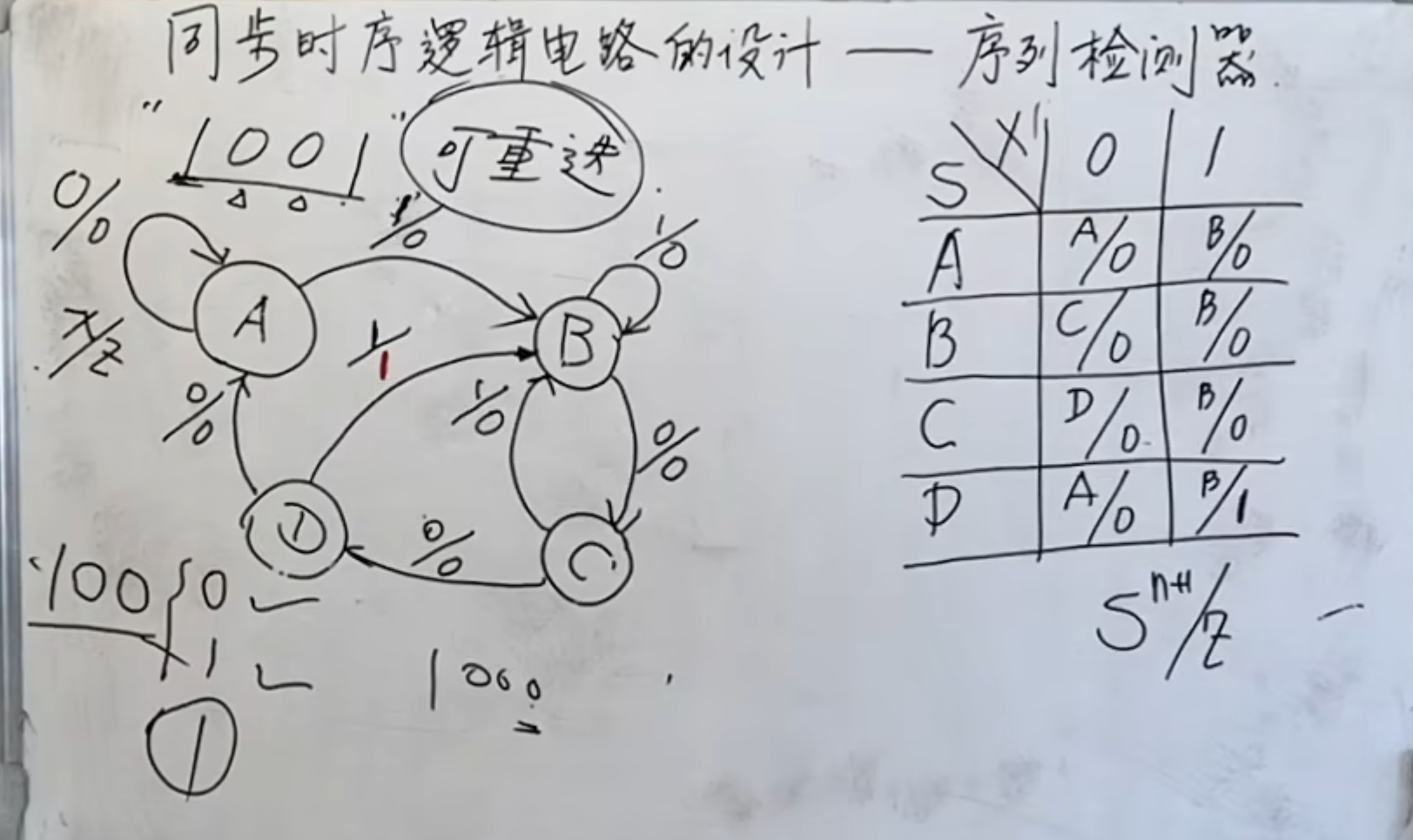
状态图和状态表如上所示。
NOTE
这里之所以是四个状态,原因在于它要检测的有四位,也就是至少要有四个状态。
而对于每一个现在的状态,对于不同的输出要做出不同的反应。、
一般来说,当在现在的状态下面,如果输入了一个对检测序列有用的,那么就需要转向下一个状态。
反过来,如果输入了一个打破检测序列的,那么就需要考虑到多层输入。
比如说,在这里要检测
如果现在的状态是
IMPORTANT
这里存在的问题是,对于
原因在于当输入为
下面就是需要分析可不可以进行化简的问题。
NOTE
如果表中的状态存在两部分的效果是一样的。那么就可以化简。
很明显,在这里是不需要化简的。
然后是进行状态分配
理论上来说,
而如何才算是好呢?
有三个原则:
- 输出完全相同,现态相邻(ABC 两两相邻,在这里是矛盾的)
- 同一个现态,次态相邻(对于
来说,它的两个次态要相邻) - 次态相同,现态相邻(在这里只有
的一个次态都是 )
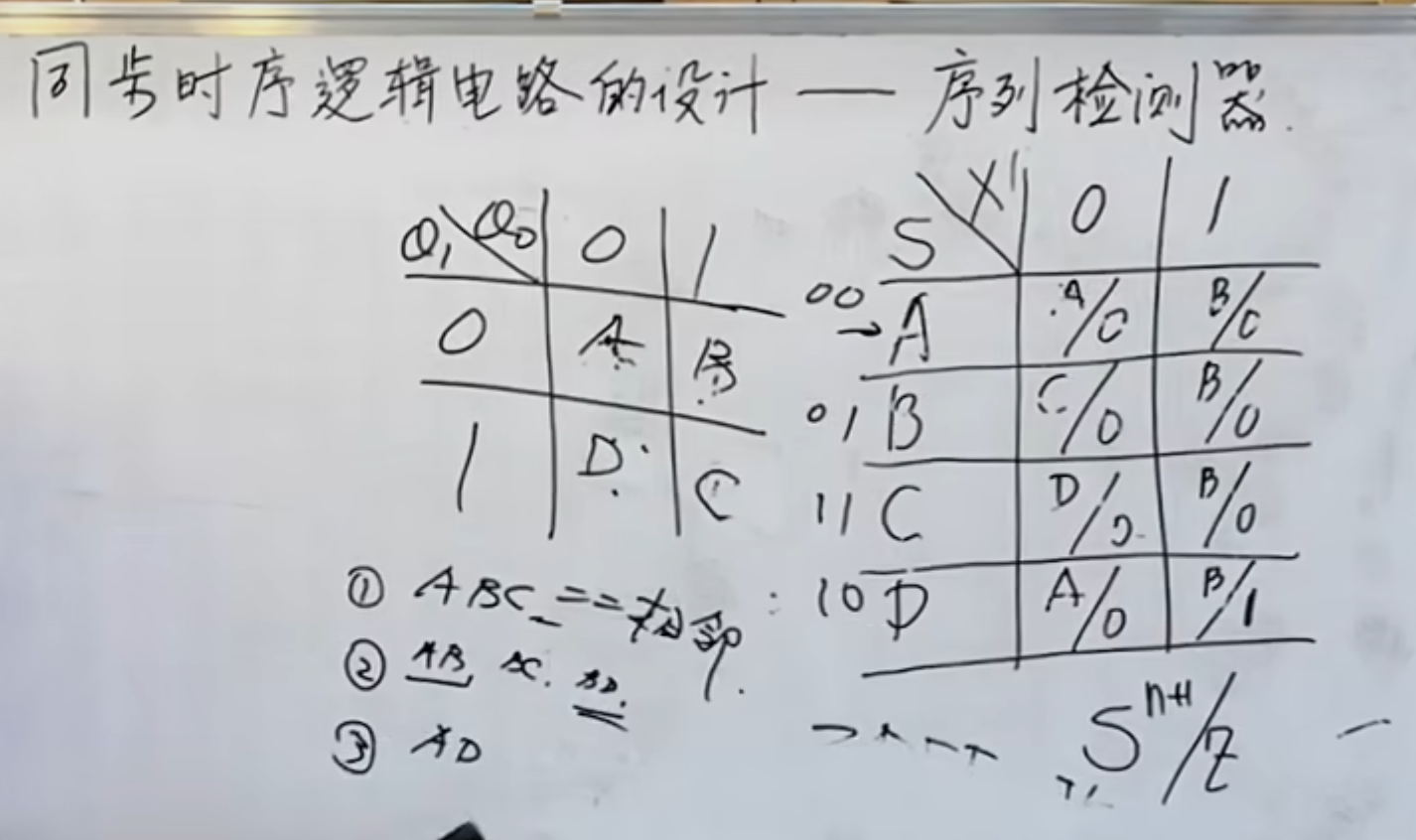
分配之后,所有
然后是根据分配的结果,得到二进制化的状态表:
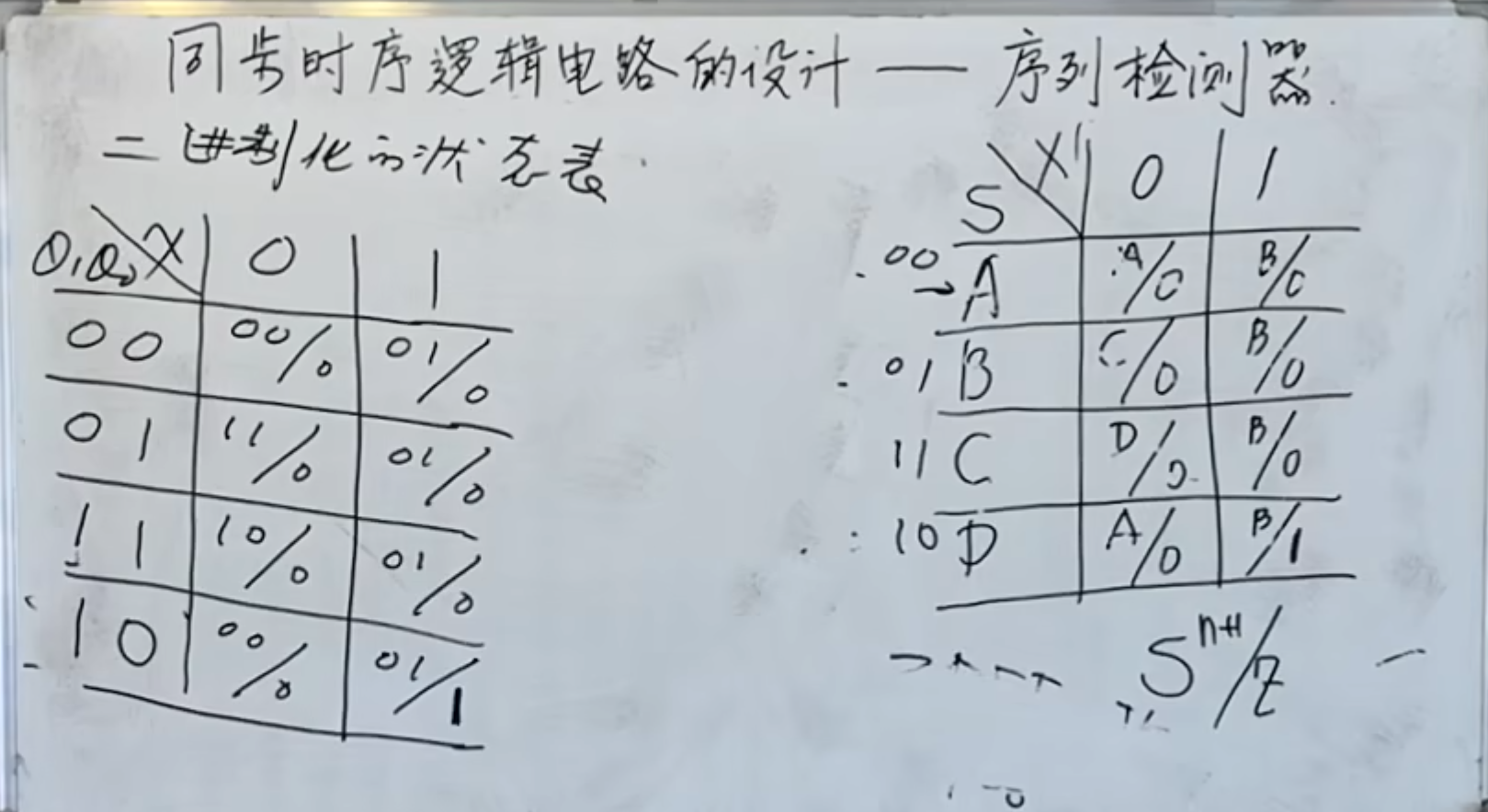
接下来是将其对于每一个输出项:
将他们的卡诺图画出来。
IMPORTANT
注意,卡诺图的变量分配顺序是按照 BCD 码的顺序来分配的:
这也就意味着,我们在提取变量的时候,必须按照卡诺图的格式来提取。
在这里,刚好
而如果
目的就是为了要得到卡诺图的状态。

得到卡诺图之后的,就是参照
将每一个的特征方程的出来:
NOTE
注意,在这里进行的不是卡诺图的化简,而是要在凑形式

最后就是将触发器的图画出来:
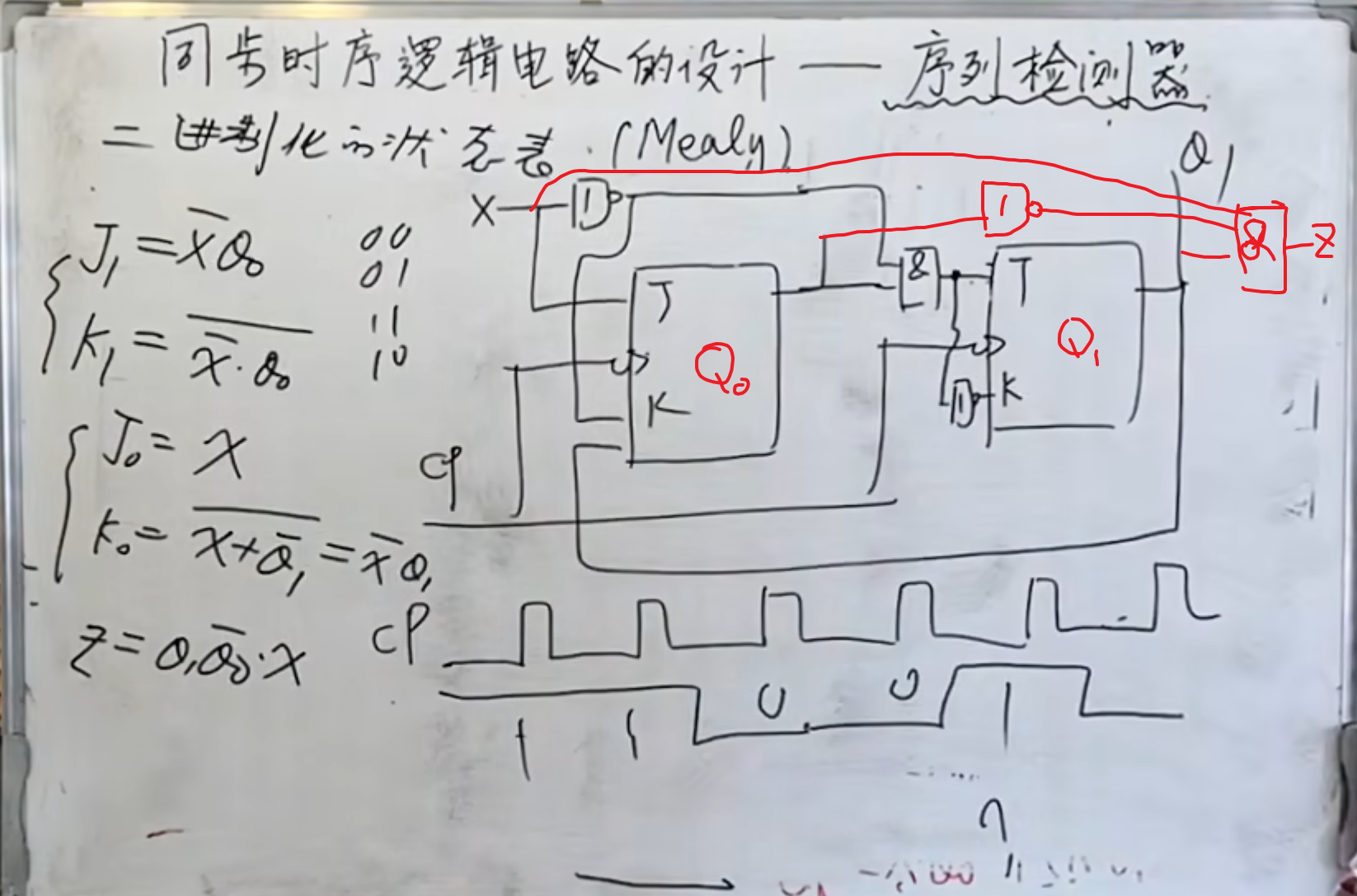
任意进制计数器
下面以五进制计数器为例子来说明:
这五个状态如果题目没有说,那就是随机的,五进制的意思是有五个状态再进行循环,并非是从 0 加到 4.
而第一步是将真值表画出来。

然后是用卡诺图来化简。
注意题目是用
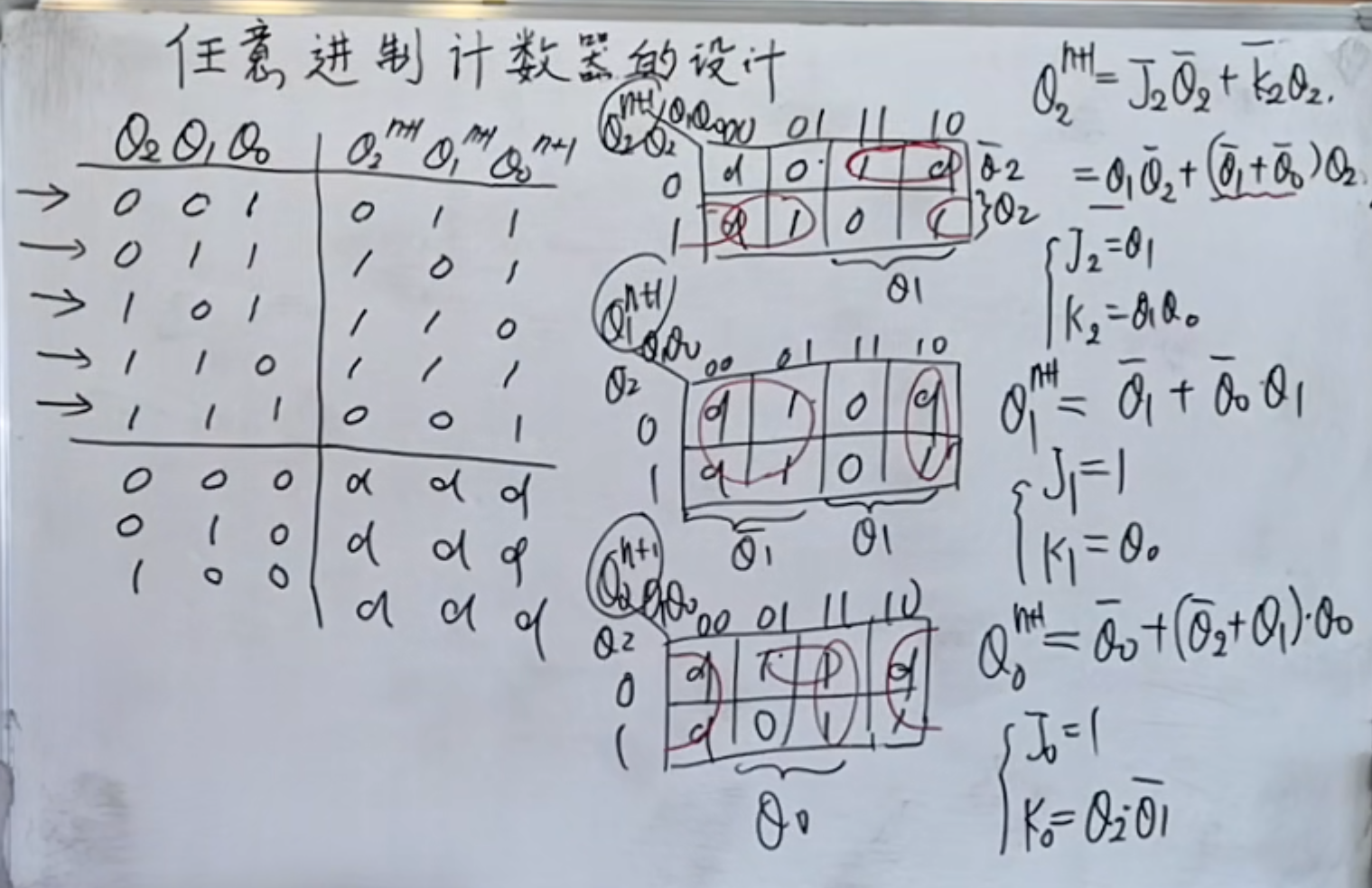
如果题目中没有提到无关状态是否会自启,或者挂起,那么一般设为
NOTE
注意,这里必须要进行分析多余状态。
一种方法是将多余的状态直接代入到特征方程中,进而得到是否能进入到循环中。
如果是用卡诺图的方法来判断,那么就之间观察这个输入对应的卡诺图上的位置是什么,如果这个值被圈起来了,代表是
所以在这里
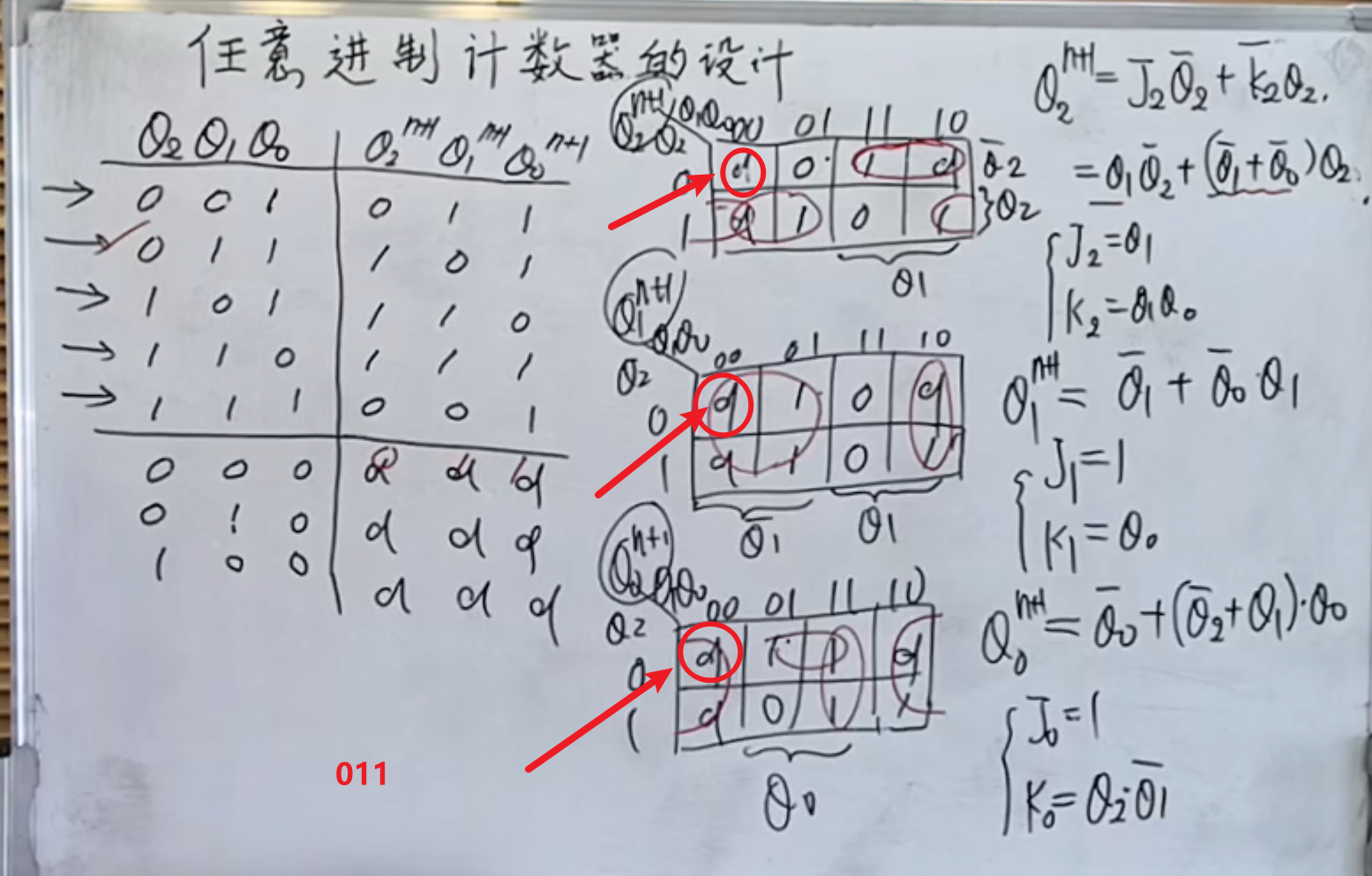
而
最后就是画图即可。将 JK 触发器连接起来。
挂起的修复
如果分析出来,存在挂起的状态,那么在设计的过程中还需要进行修复。
下面还是以一个例子来分析:
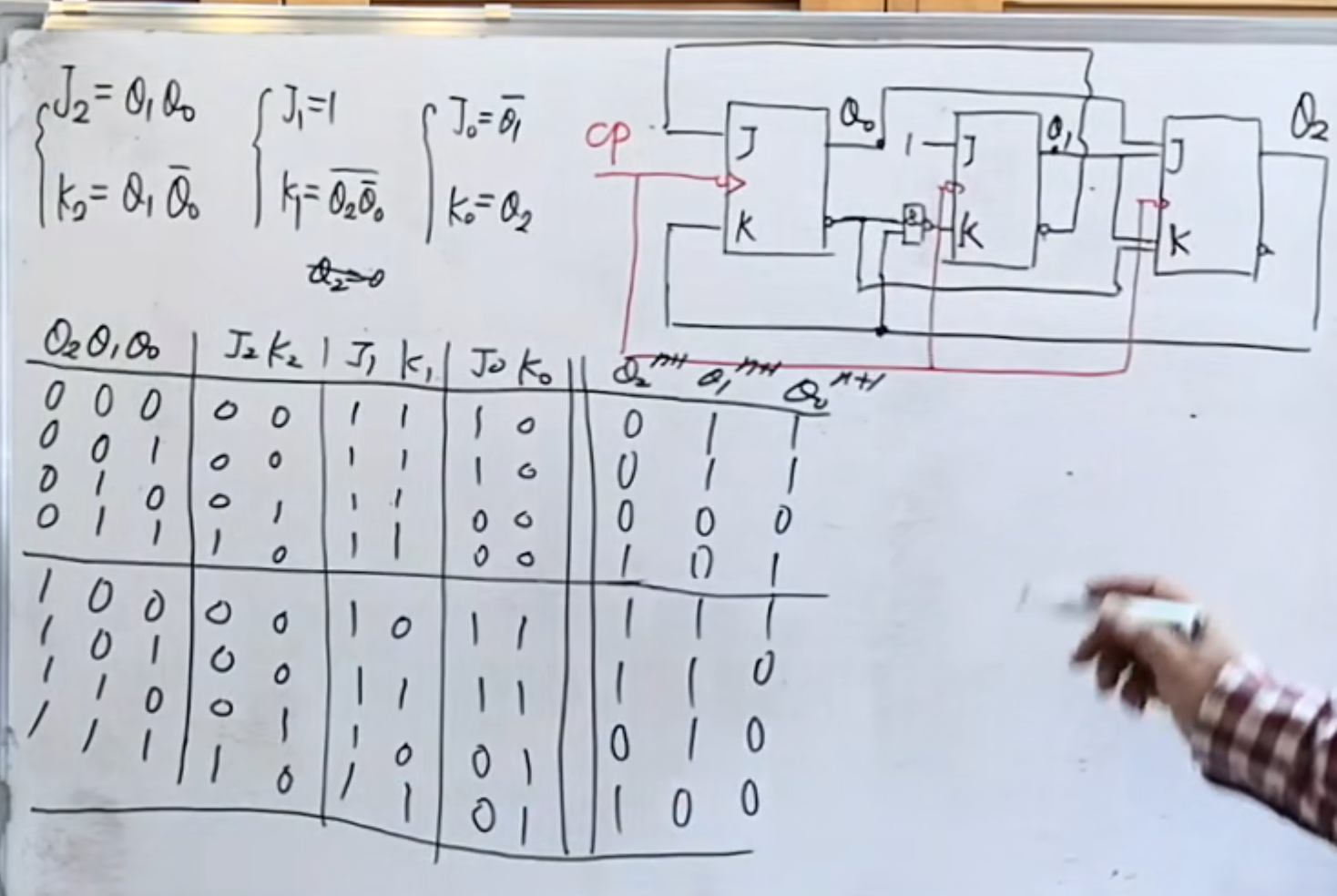
首先在得到电路图之后,要先把特征方程写出来。
然后利用特征方程,再将状态转换真值表列出来。
然后是状态转换关系表、关系图:
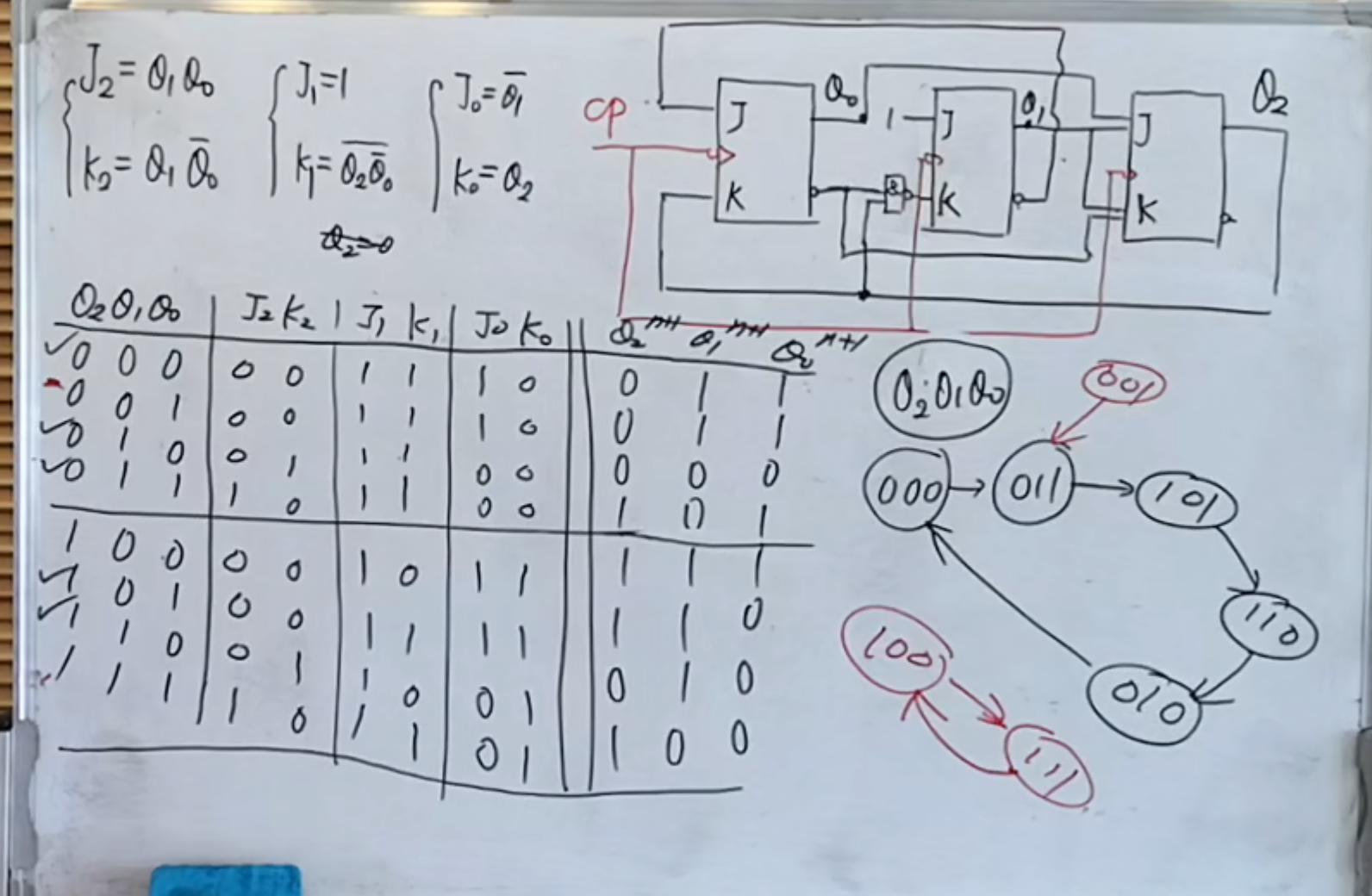
然后可以发现出现了挂起问题。
NOTE
解决方法则是将其中一个状态的次态变成循环中的任意一个状态即可。
例如将

因为改变的是
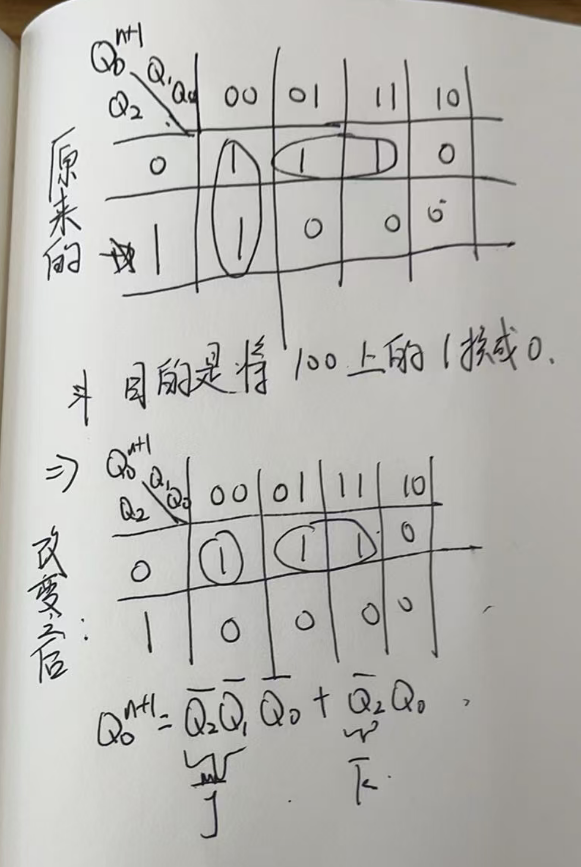
然后再按照改变之后
状态化简
状态化简主要解决的问题是将电路中可能出现相同作用的部分统一起来,减少元器件的使用。
等价状态
NOTE
等价状态,这里指的是现态相等,如果满足下面的条件,则可以得到现态相等
有两个条件:
输出完全相同
次态等效
首先是输出完全相同,这部分比较起来还是比较简单的。只需要看最后的结果即可。
然后是次态等效,这里又分成好几种情况:
第一种是次态相同,或者各自维持原状。

NOTE
维持原状的意思本质上是次电路实现的公式是一样:就是保持输出不变。
第二种是次态交错:

第三种是次态循环
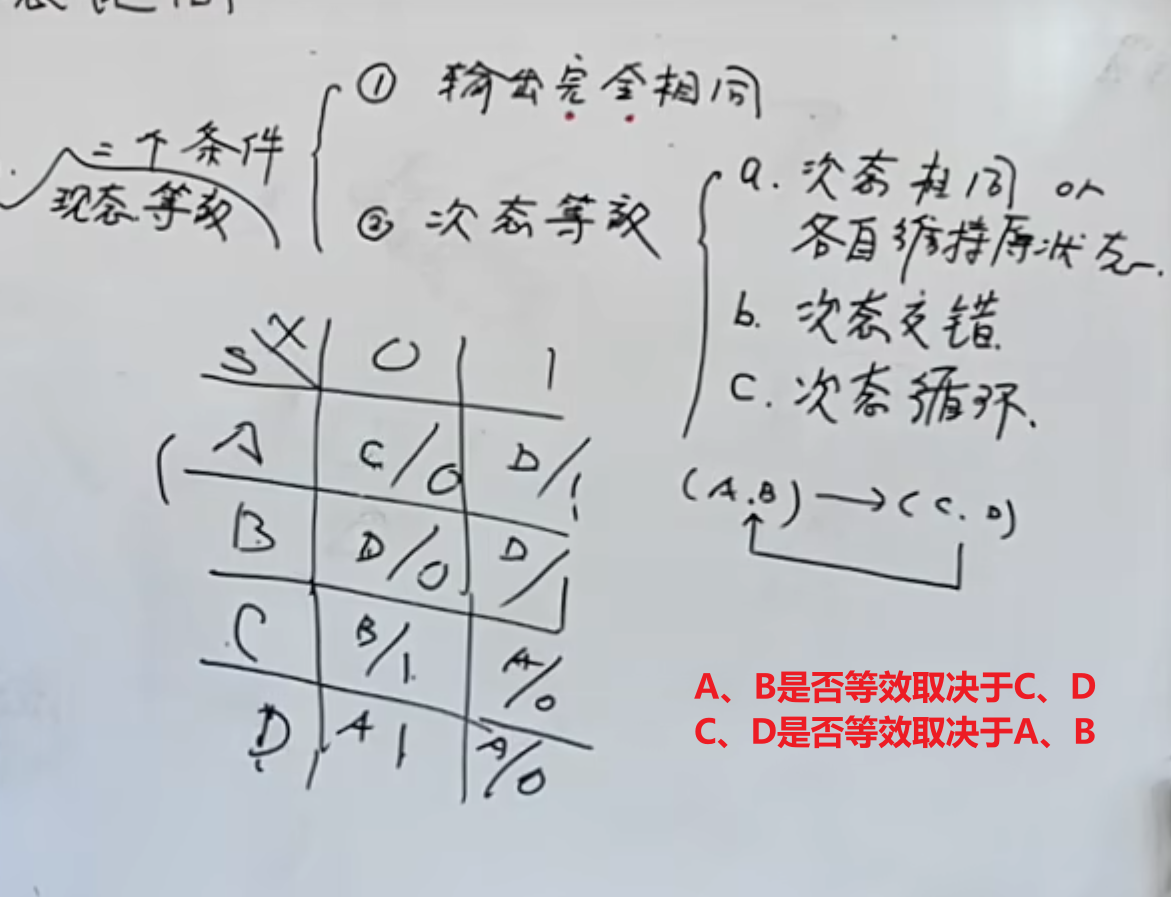
更复杂一点是:

这就构成了循环次态。
但是,如果最后面的
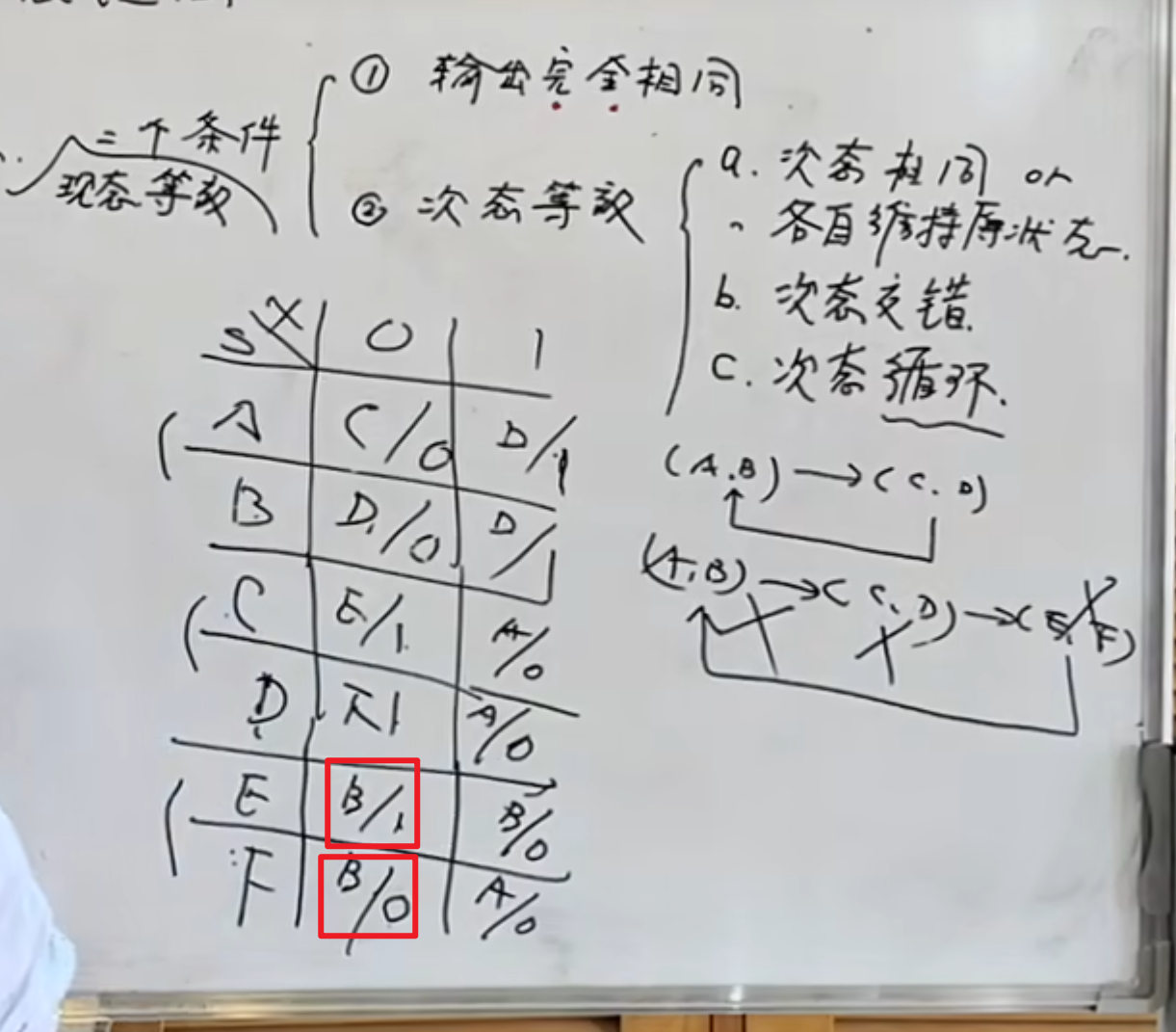 \
\
等价特性
传递性
等价类
等价类是等价状态的集合
比如上面的
用集合的形式表示就是:
当然如果
最大等价类
最大等价类就是我们最后要找的目标。
例如:
例子
下面这个例子是比较简单,可以直接看出来。

第二种方法是针对比较复杂的情况:使用的方法是隐含表法
隐含表法
NOTE
方法叫做:取“头”少“尾”
列一个表,形如:

方法是:
- 做表
- 顺序比较
- 关联比较
- 写出最大等价位
下面用一个例子来说明:
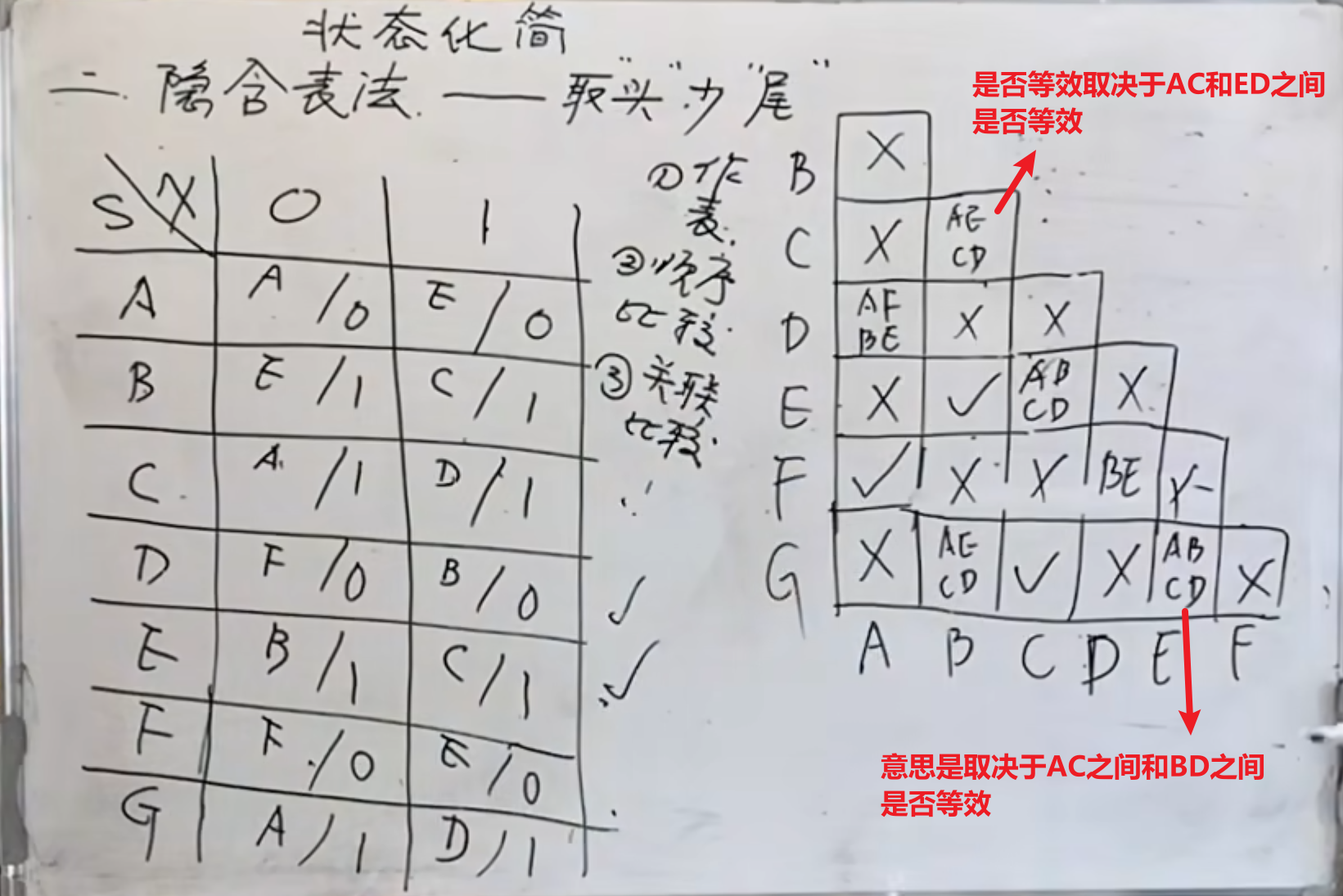
到上面这个表这一步已经完成了前两步,接下来是后面两步:
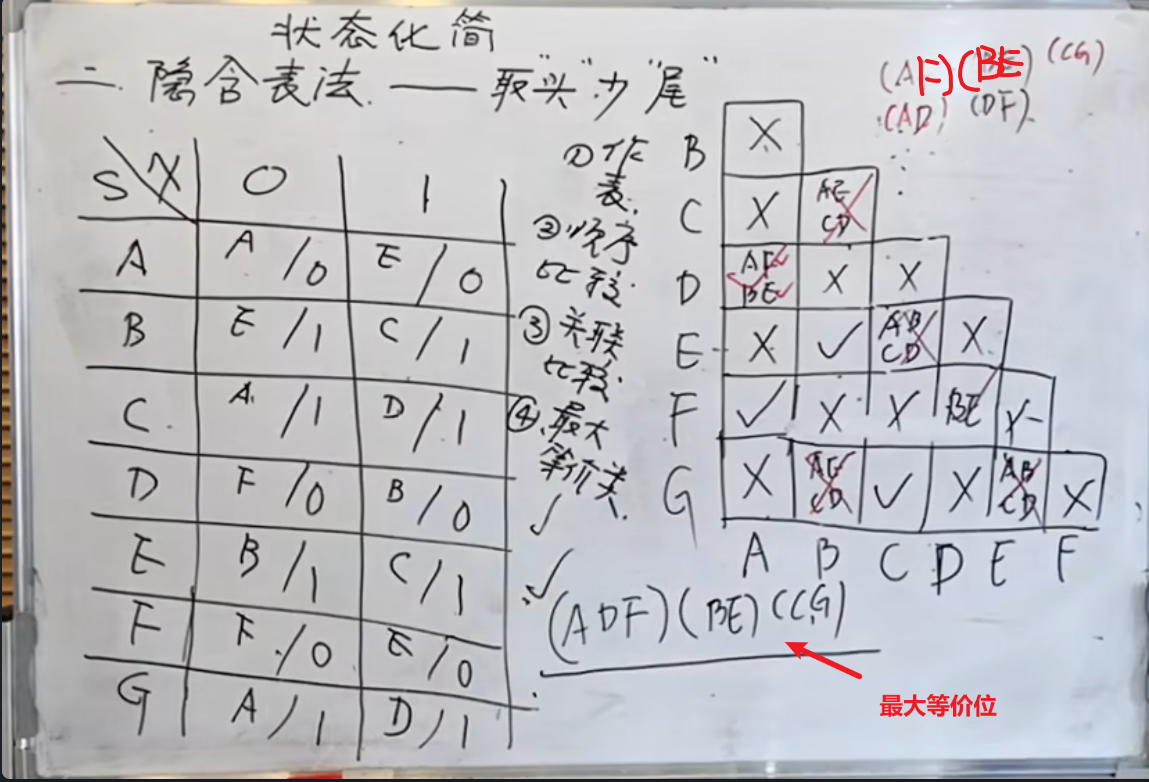
先将上面表中需要进行判断的判断出来。
然后是利用传递性将最大等价类求出来
得到最大等价类是:
然后在用得到的这三个最大等价类画一个新的状态表。
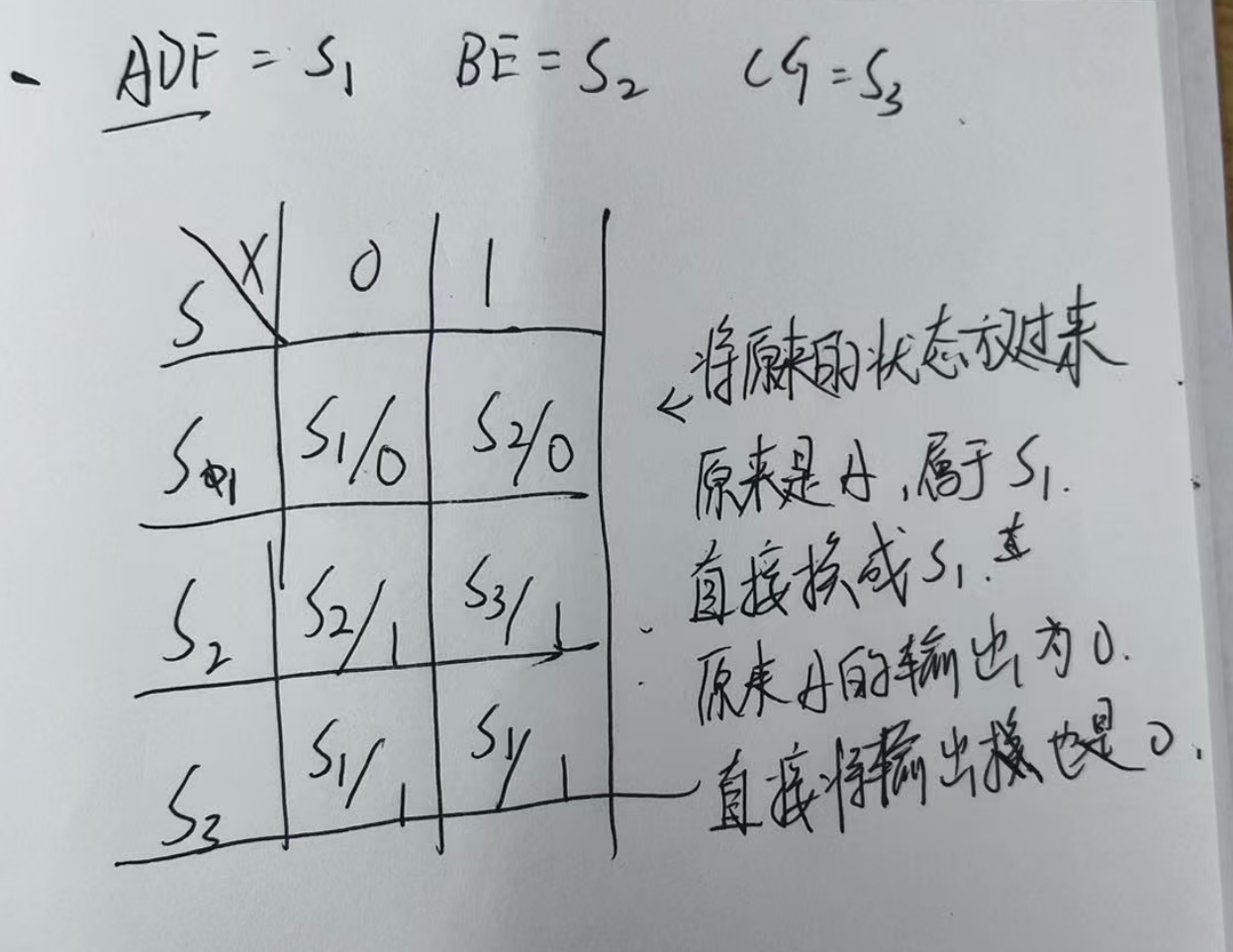
NOTE
还是要对着原来的表将最大等价类的表画出来。
注意替换问题:
以
次态则也是由
只需要理解他们都是等价状态(次态和输出都是一样的)即可
再来一个例子:
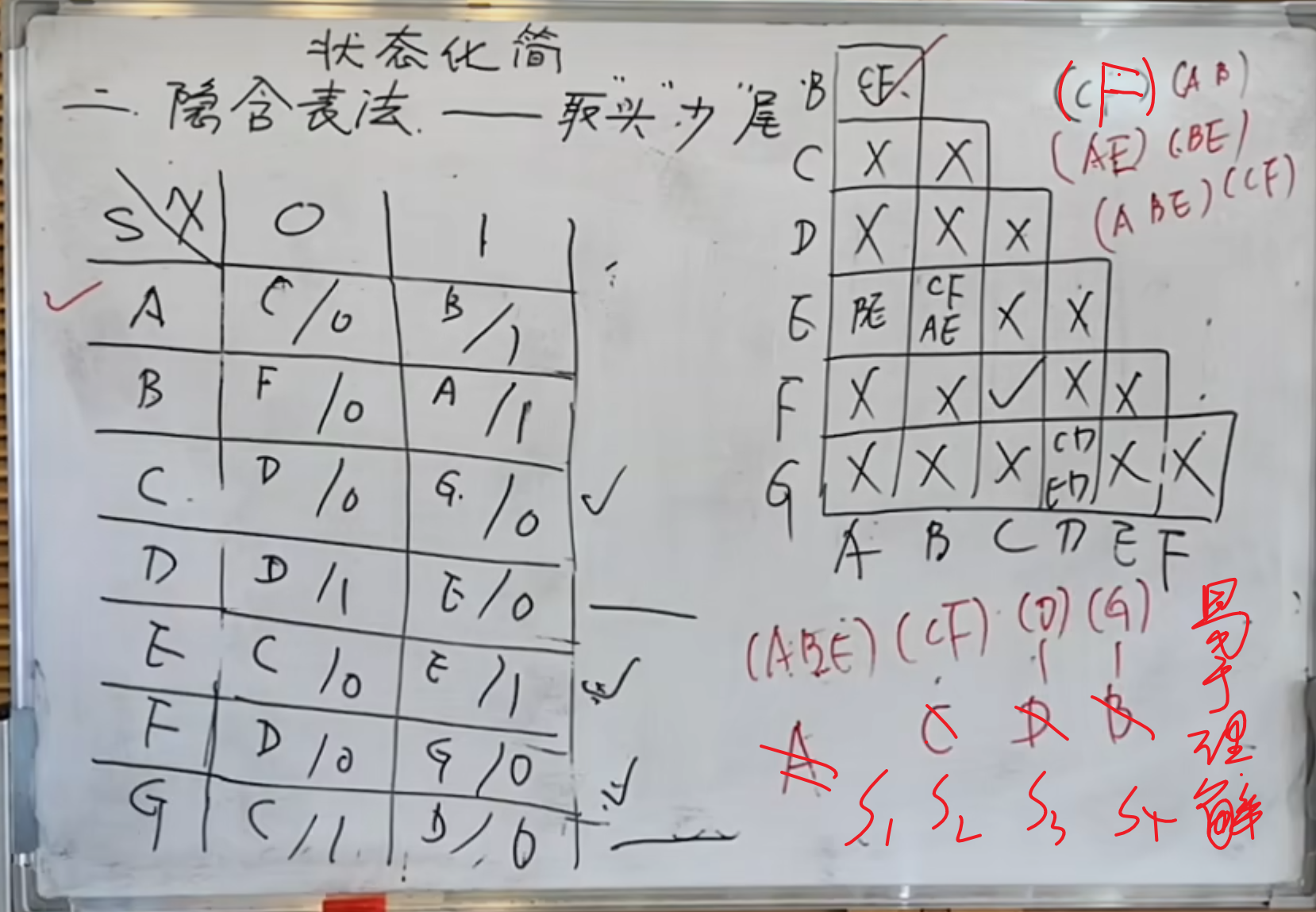
然后就是画出改进后的状态图。
设计中 Mealy 型和 Moore 型的区别
常见的输出与变化有关的是
而
所以在画图的时候,

NOTE
注意,在这里的,这两种形式的区别还是比较大的。
因为
而
当然也要具体情况具体分析
异步时序电路的设计
IMPORTANT
这部分不算是重点
流程上还是一样,依然是先画出状态转换图或者状态转换表。
而在过程上,用触发器的激励表来显示比较合适。
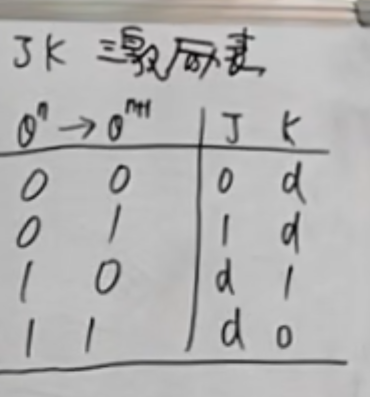
NOTE
而在过程中,我们发现,在进行状态转换的时候,我们将其中一部分的触发器的
下面用例子来说明:
首先是高位的触发器。
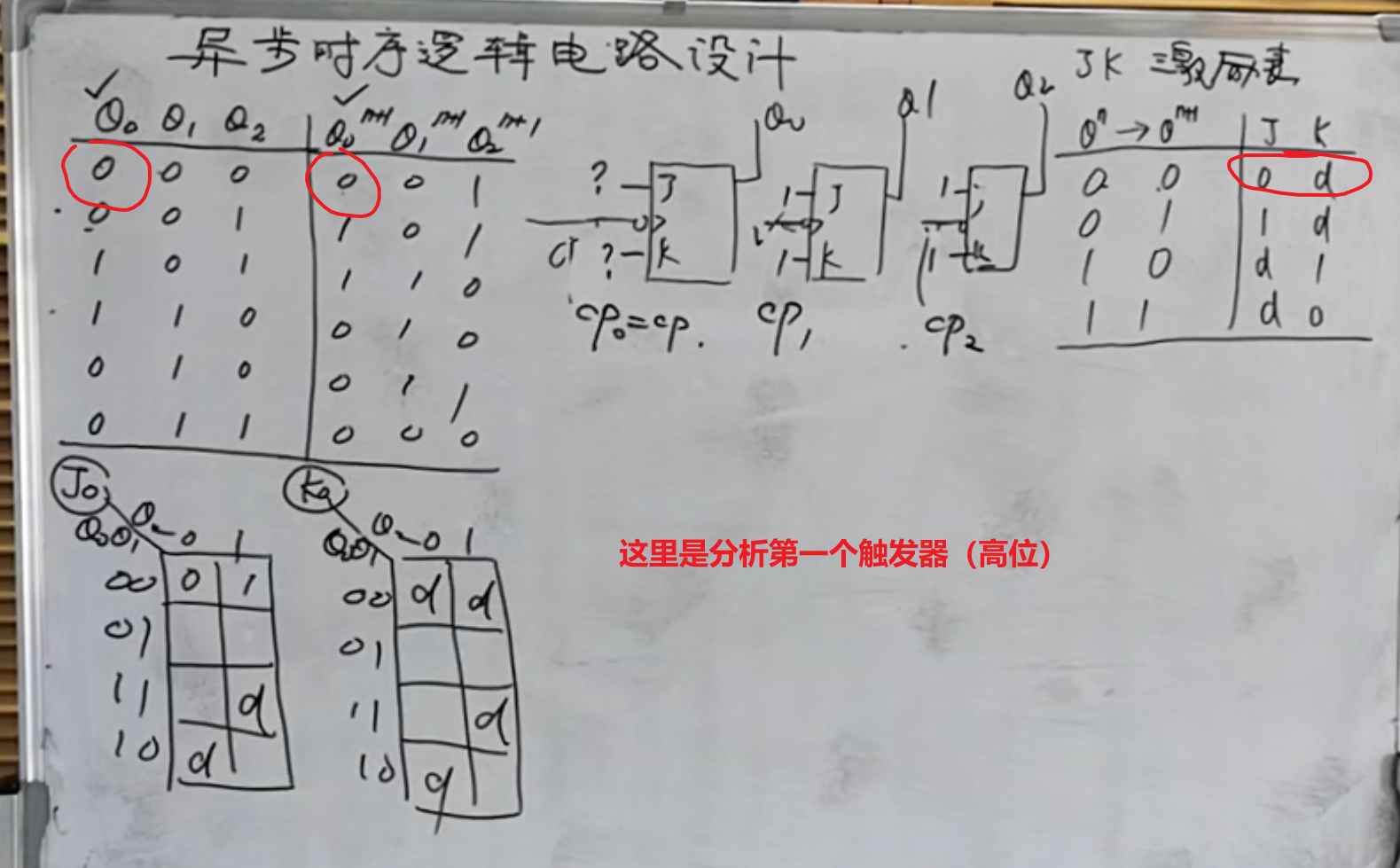
由于这里依然是按照有外部
从

这一部分,完全是按照同步时序逻辑电路的设计方法来实现的。
下面则是来设计
这部分的电路设计的主要依据是当有
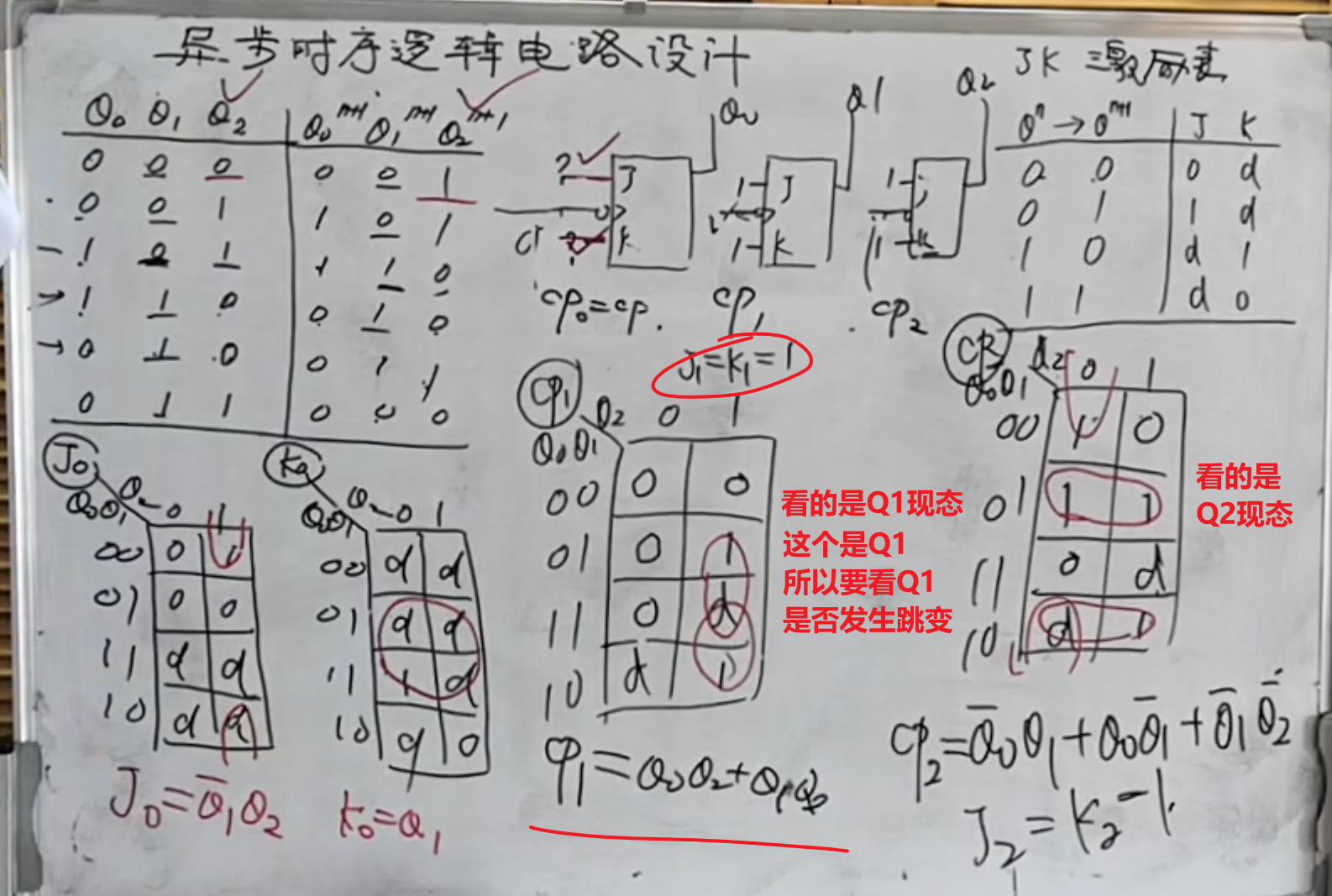
IMPORTANT
总体的设计思路就是令其中的至少一个为同步时序逻辑电路设计。
其他的触发器让
这里发现对于
首先是无关项,这个直接先写上,然后是分析
然后是分析当
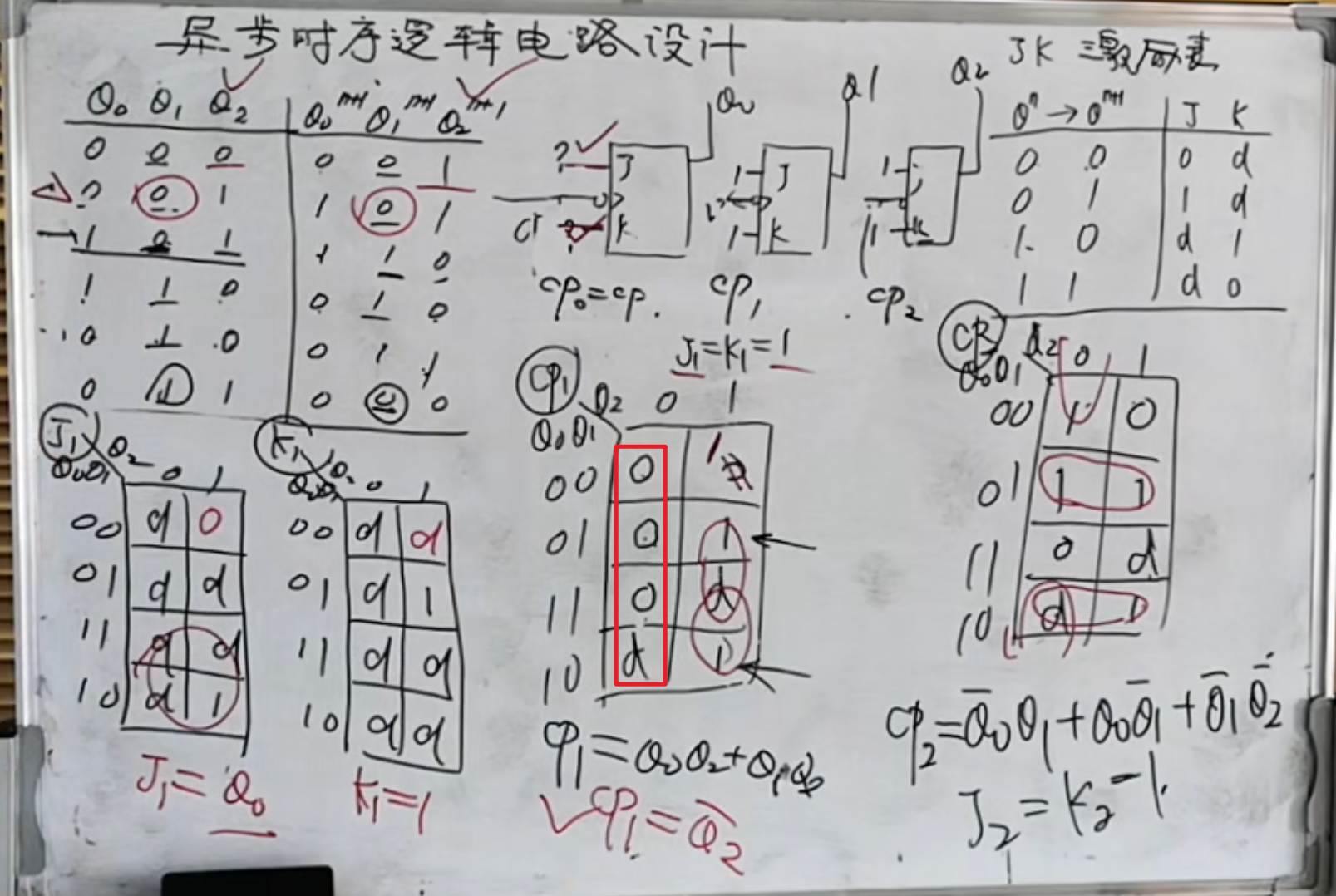
然后是
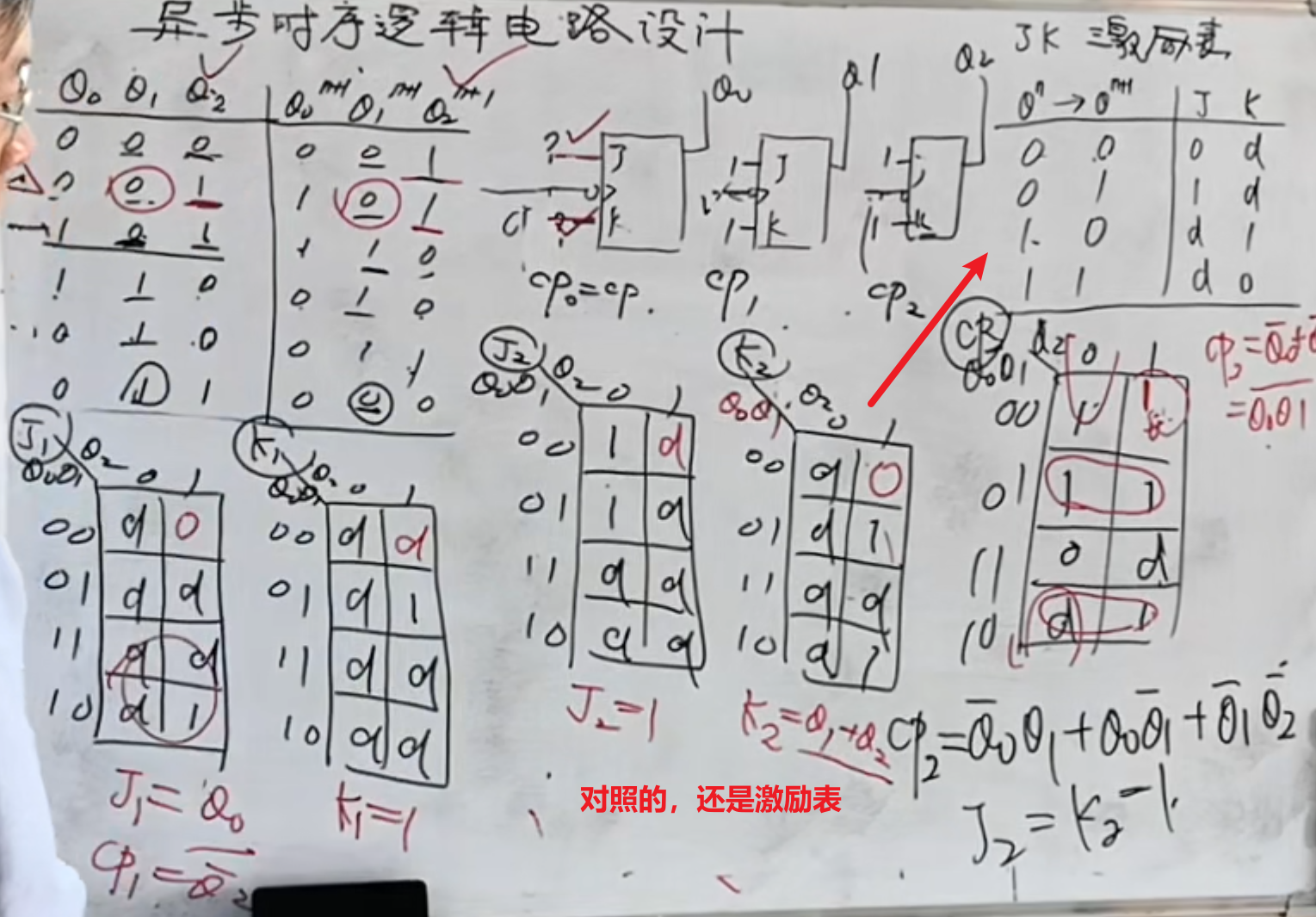
当然,除此之外,可以直接让
这样总体上来看也是异步的。
时序逻辑集成电路
寄存器
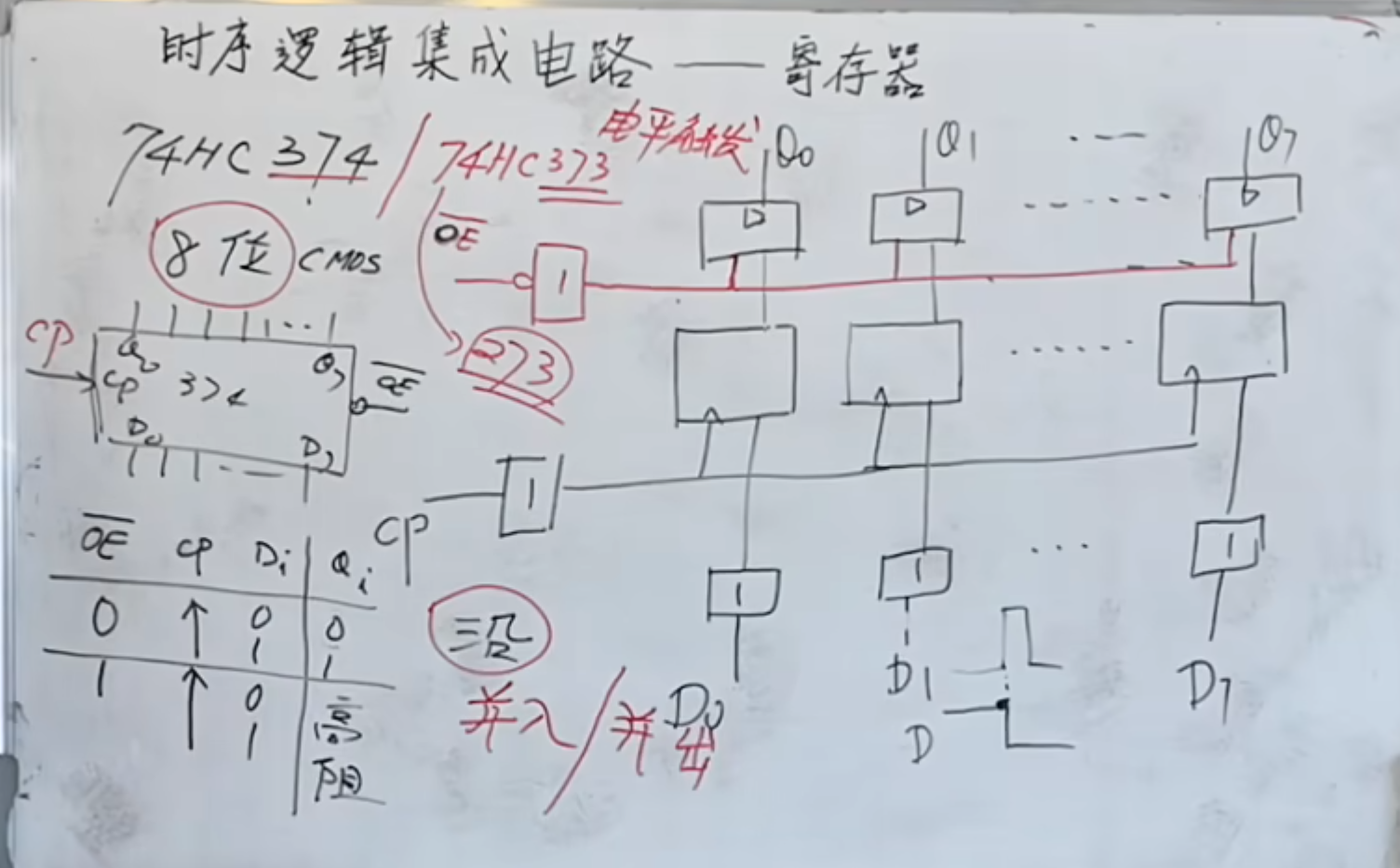
芯片为 8 位 CMOS 74 HC 374
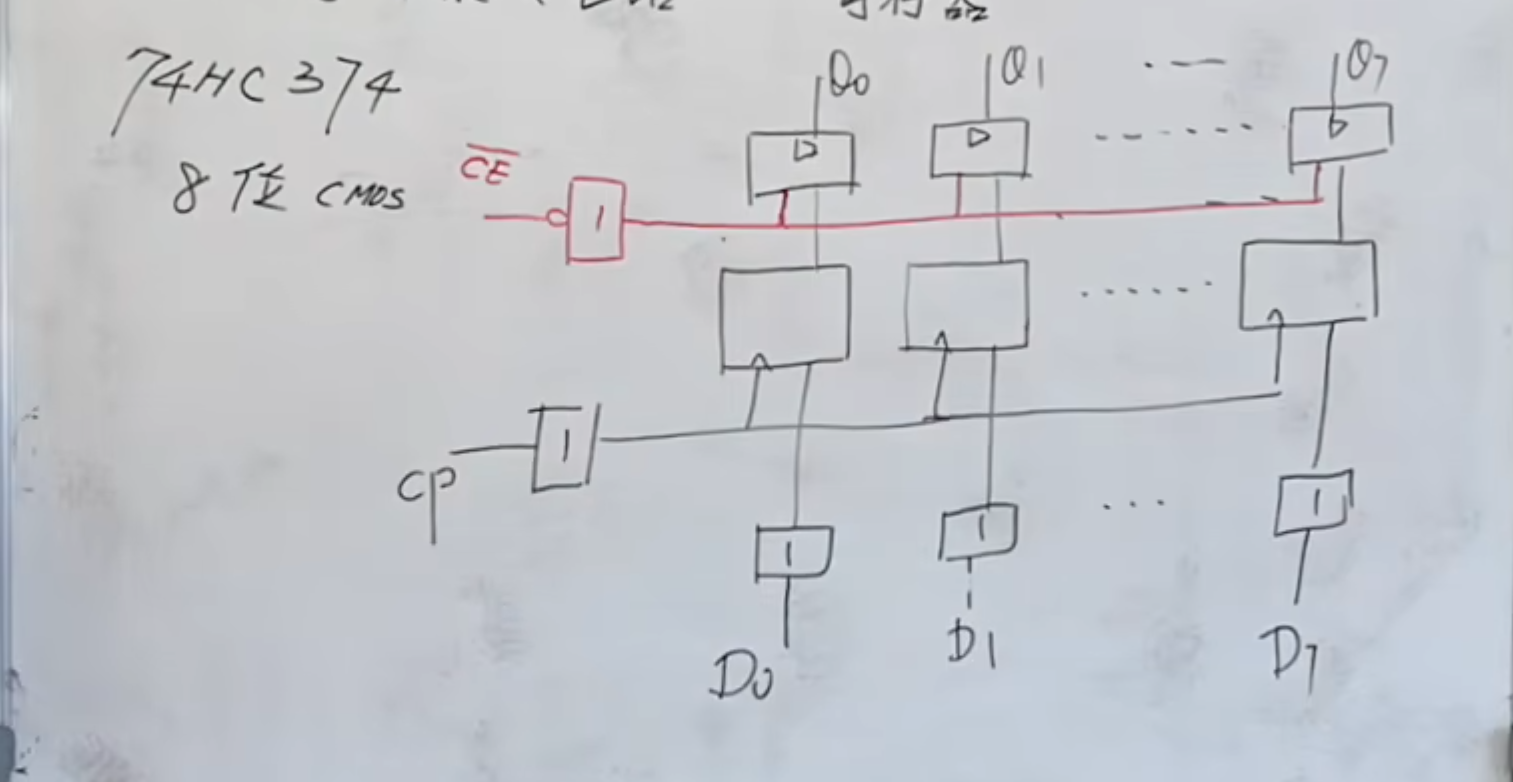
上面这个图是内部结构。
主要是由
并且这个是一个并入、并出形的结构。并行输入,并行输出
此外,这是一个边沿触发,(上升沿触发)
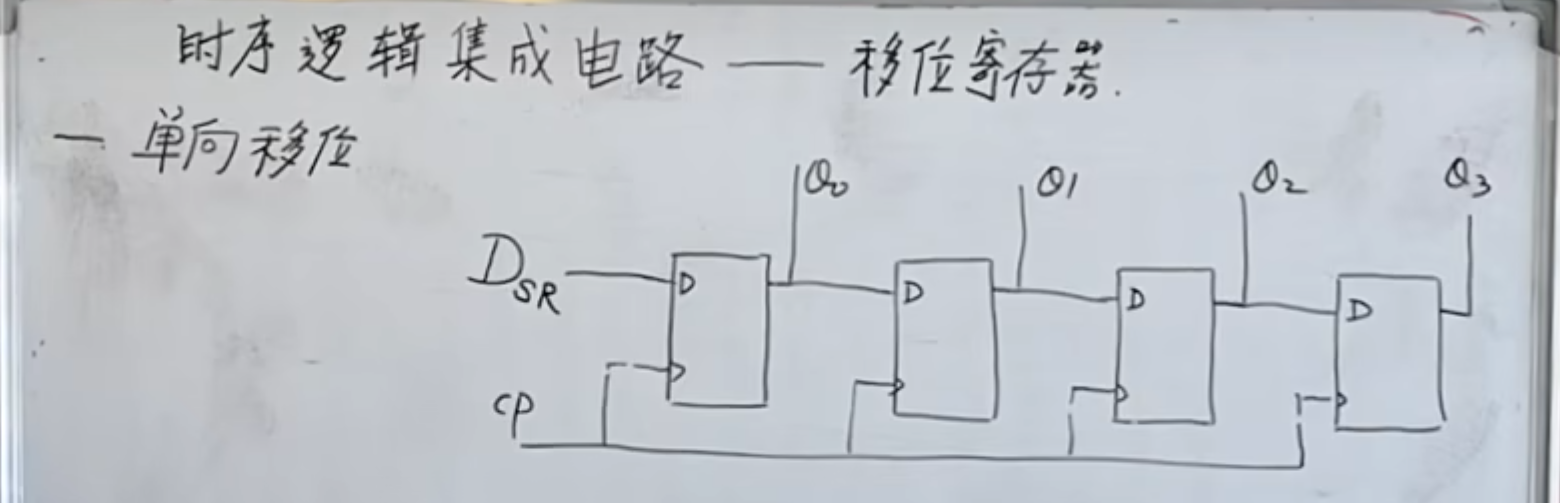
移位寄存器
单向移动
NOTE
这里将
从低位向高位移动,因为低位在左边,所以叫做右移
反之,从高位向低位移动,低位在左边,就叫做左移
单向移动,就只能是左移或者右移
不同教材上,针对向右移动的定义是不一样的,根本区别在于低位在左边还是右边。
在这里,如果输入为
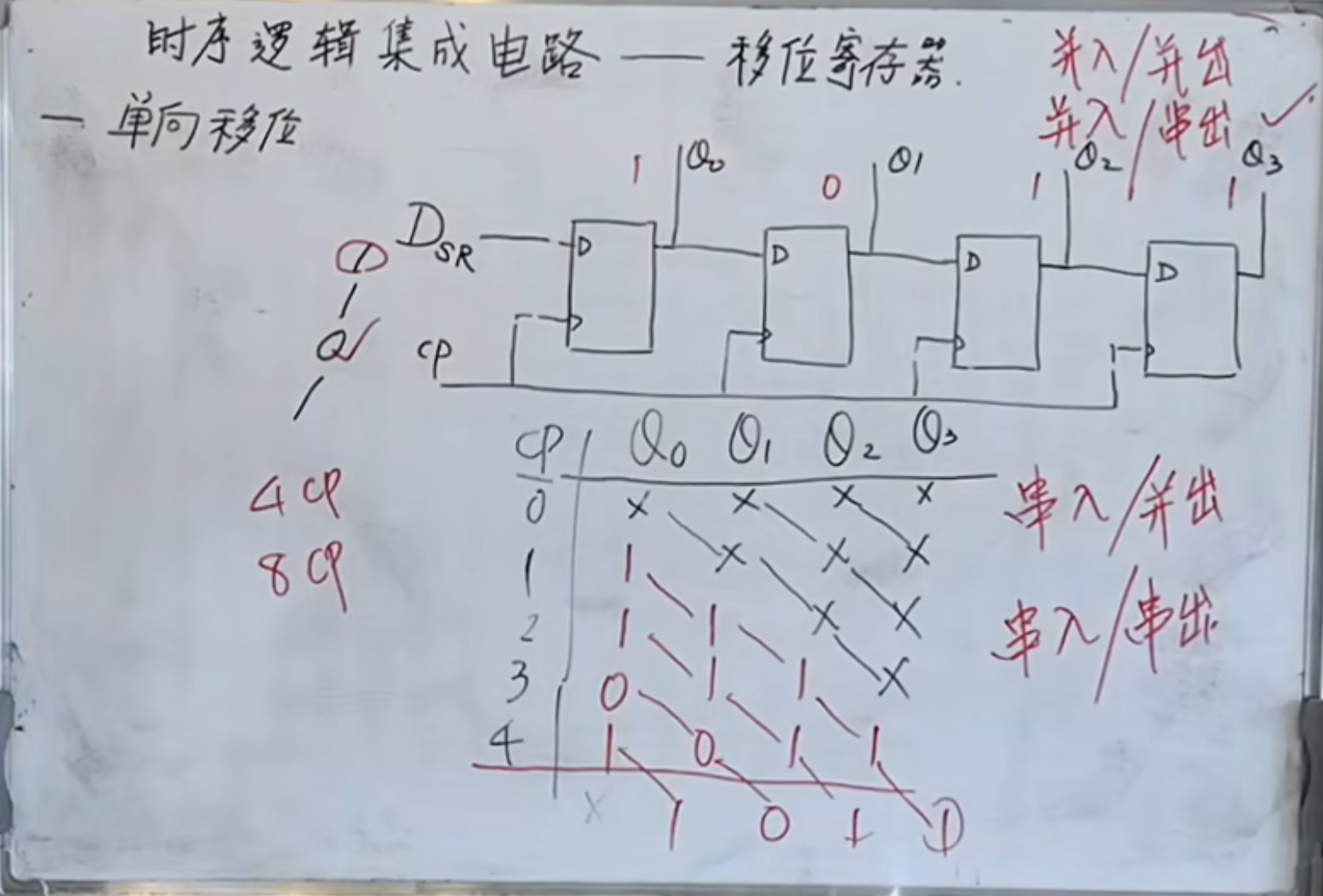
当来到第四个脉冲
综合起来叫做串行输入,并行输出
此外,当最高位一位一位输出的时候,这就叫做串行输入,串行输出。
如果是
集成块 74 HC 164
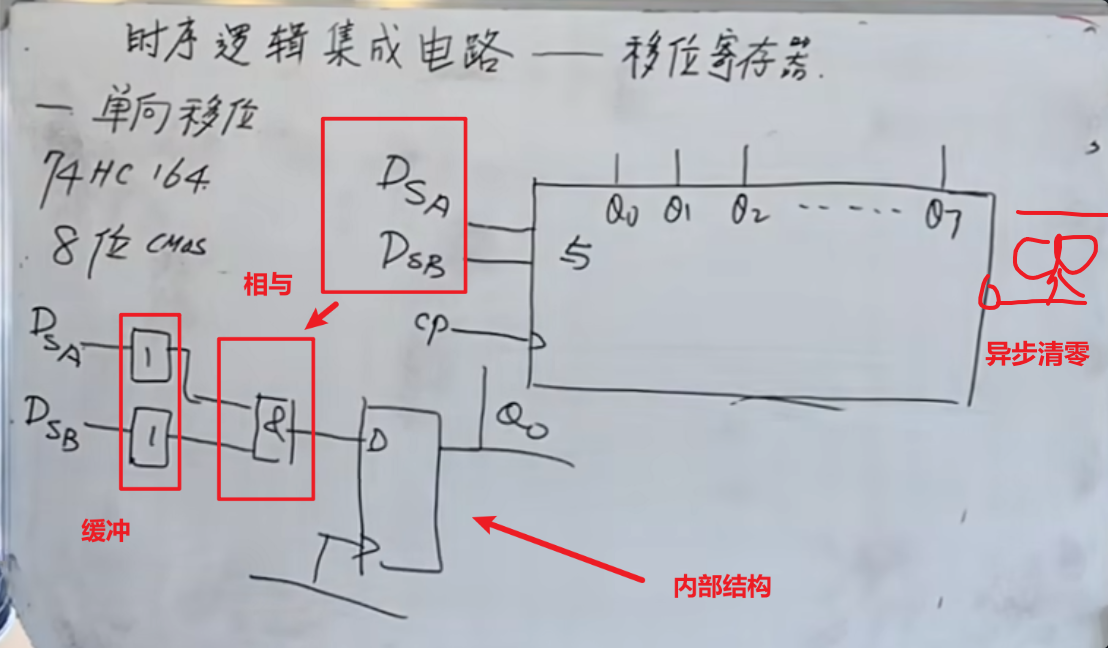
其中的
下面是一些移位寄存器的应用:
如果将高位的
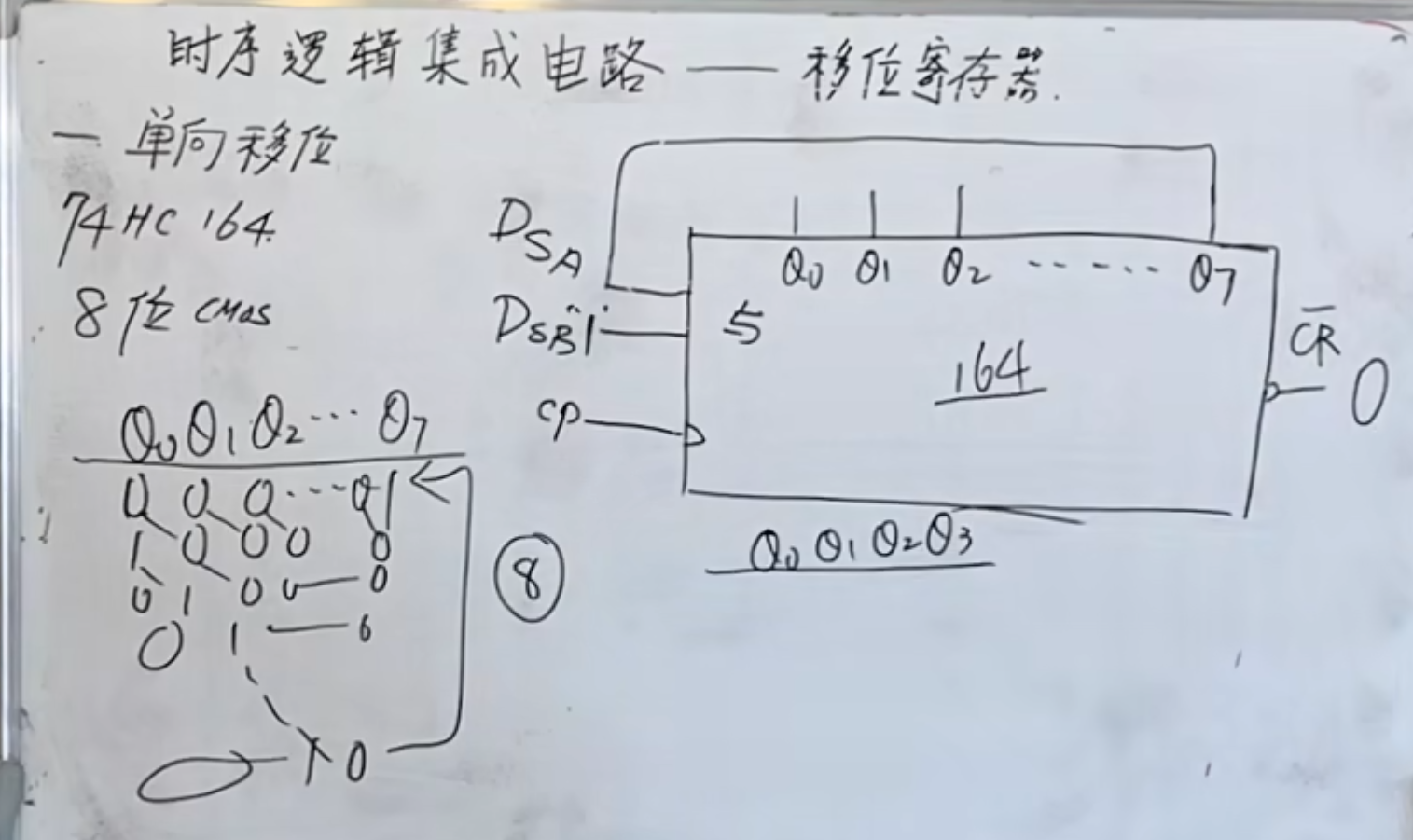
如果在连接的基础上加一个非门,那就形成了钮环:
原来如果是
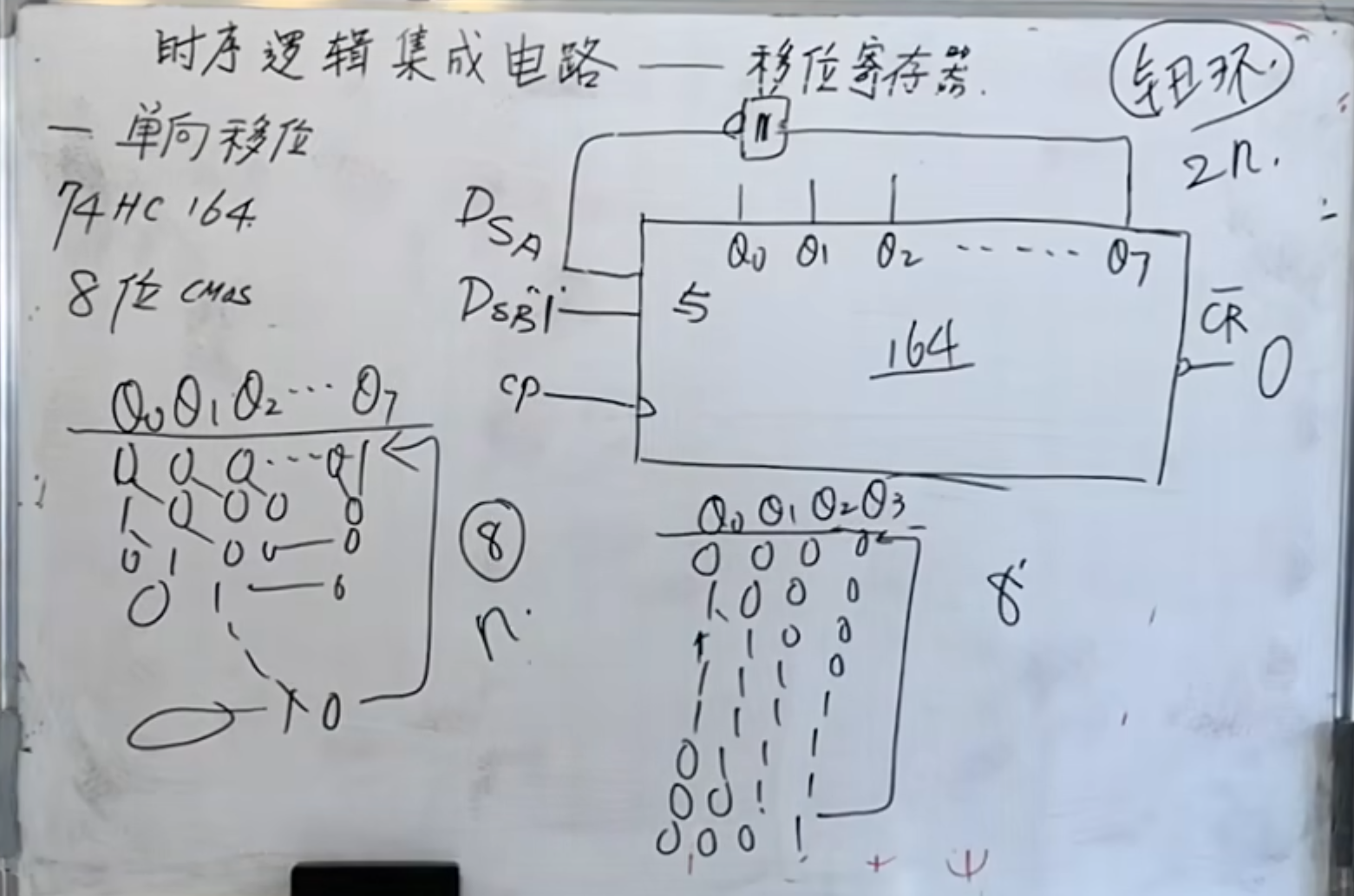
双向移位
即能左移,也能右移。很明显,需要一个控制端来对左移还是右移进行控制。
而这里就是使用二选一数据选择器来实现。
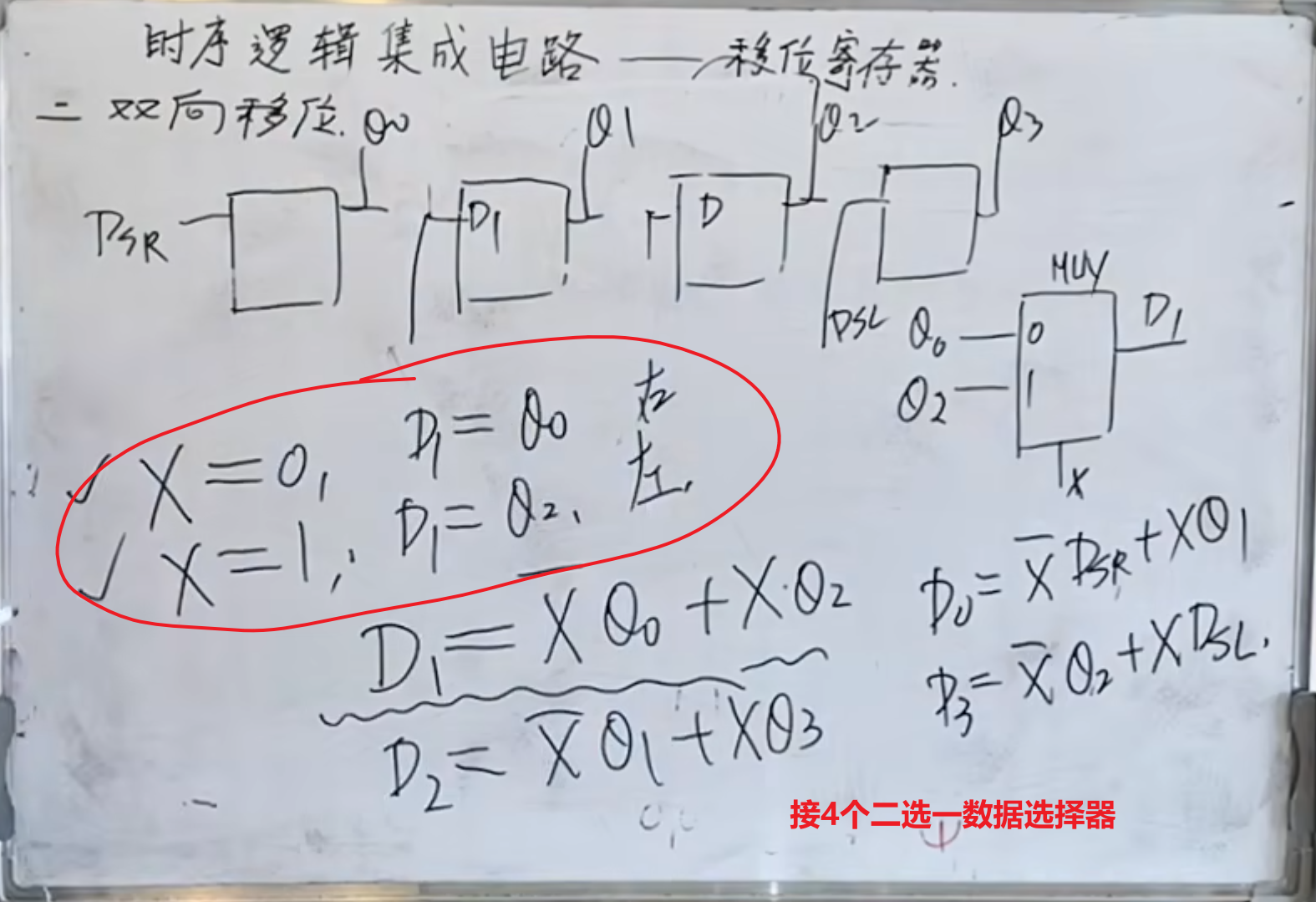
而对于实现此功能的集成电路是 74 HC 194
集成块 74 HC 194
194 这个芯片比较重要,它有四位输入,四个功能。
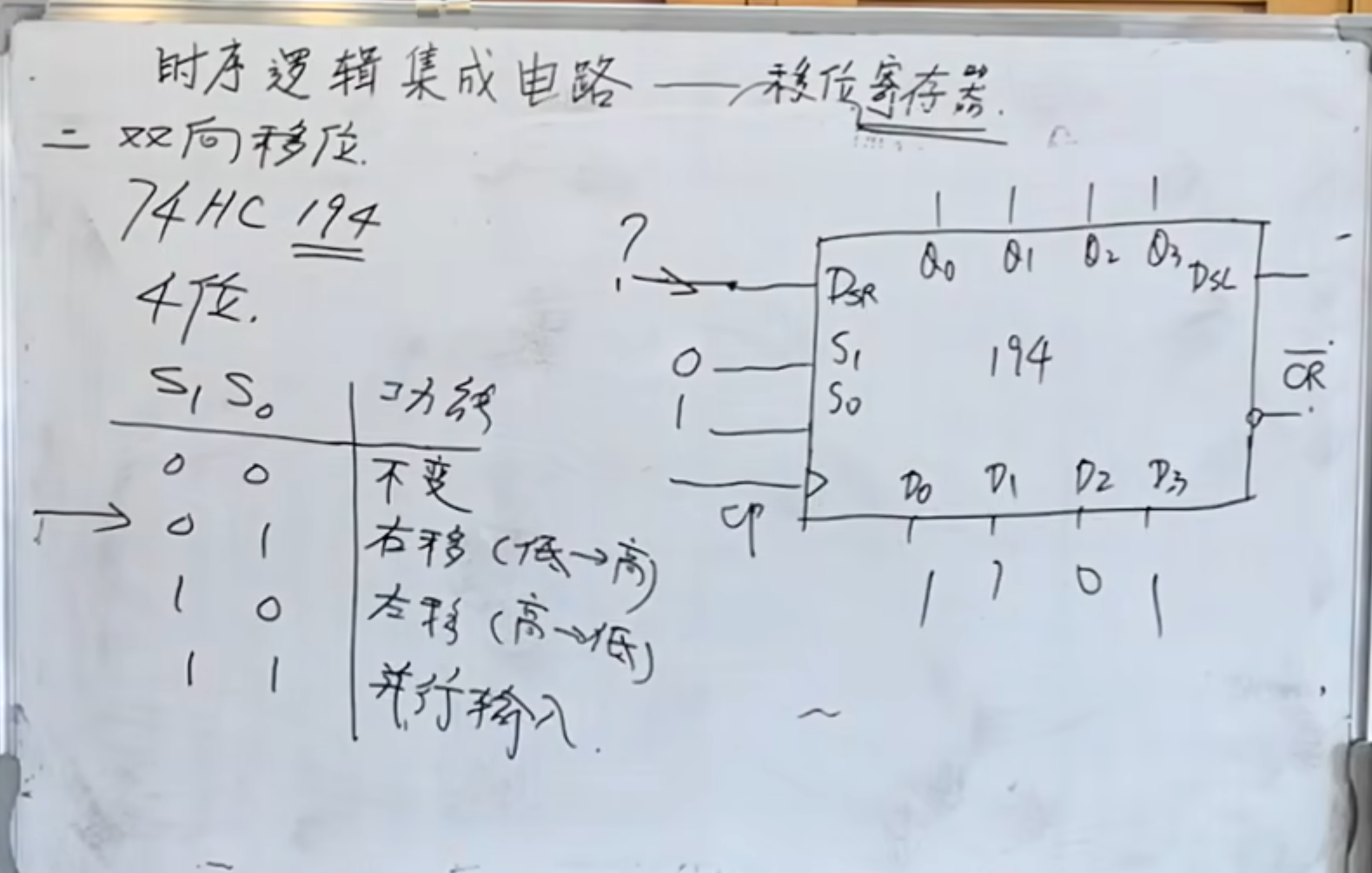
分别来看这四个功能:
首先
就不需要考虑:是保持不变。 然后是
,实现的功能是将 、 、 、 的输入,从 、 、 、 输出。 下面是
, 代表着左移,意味着是从高位向低位移动(这里的移动指的是下一次脉冲来之后,相对于上一次脉冲的四个输出的位置。)需要在 上加入数据。 是类似的。是右移,意味着是从低位向高位移动。需要在 上加入数据。
此外还要清零端
194 的应用
在左移或者右移的过程中,将其中的几个输出通过一些门电路,然后接到输入上。
本质上是构成进制计数器。
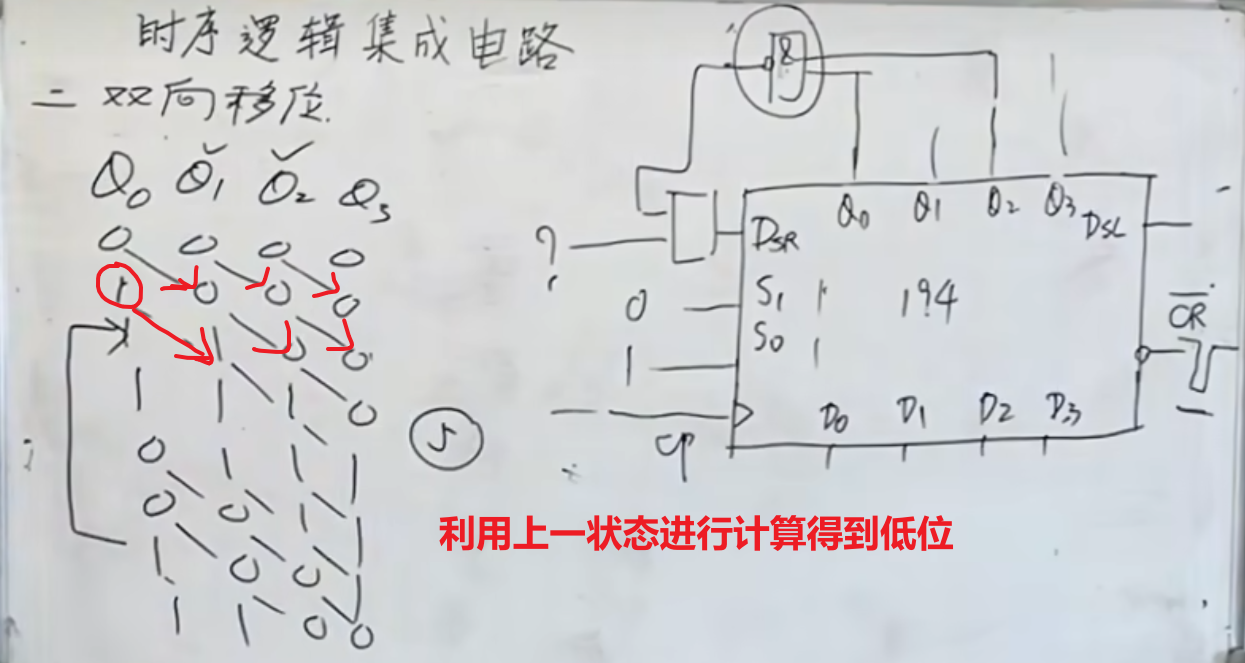
NOTE
如果是右移,那么如果初始值为
左移也是一样的,如果初始值为
这里所谓的根据上一状态计算得到低位,是根据连接的方法计算得到的。
比如在上面图中,
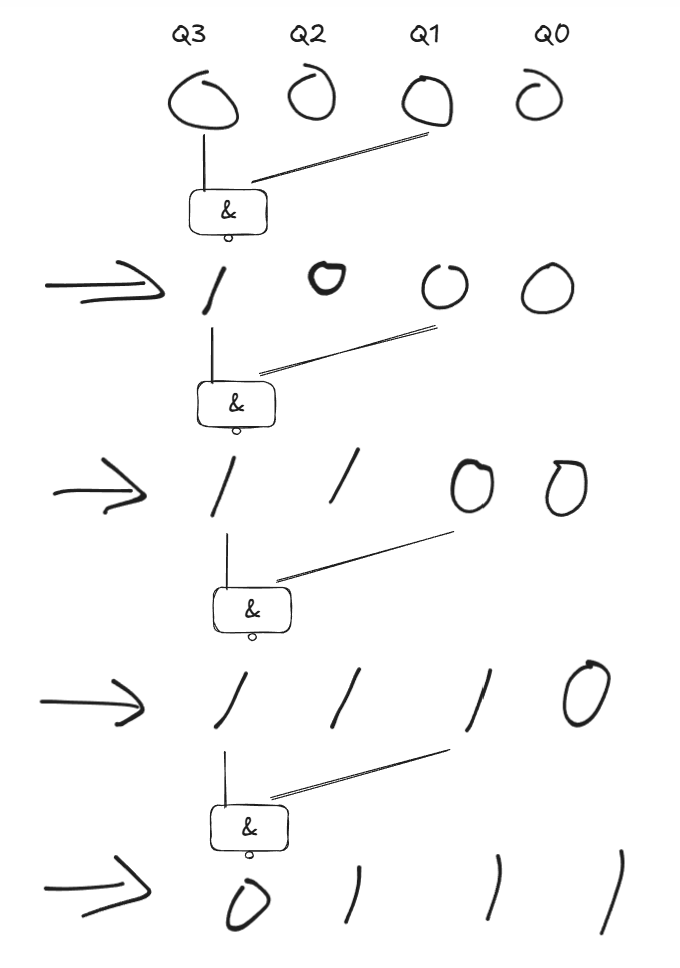
NOTE
这里有点规律。
如果是将相邻的两个与非到一起作为最低端的输入,那么一般都是奇数进制计数器
如果是间隔一个的两个输出与非到一起作为最低端的输入,那么一般是偶数进制计数器
当然,这里接入的可以是随意结合的门电路,当然,本质上还是循环移位。所以只需要判断最低位上的变换即可。
161 四位十六进制计数器
IMPORTANT
161 的功能控制有两种表示方法:
一种是
还有一种是
注意区分
NOTE
计数和分频之间的关系是:
如果要做
其中,

四位十六进制计数器 - 161
一般来说,同步计数器使用的范围比较大,异步计数器不怎么用
功能表:
NOTE
异步清零,同步置数
在这里清零是不需要看脉冲的,只要清零端有效,立马变成零

其中
NOTE
计数:不需要考虑输入是什么,只要满足计数的条件,那么来一个脉冲,就开始从
而当

实现十六进制以内的计数器
这里实现任意进制比较简单,只要是在计数状态下,那么输出计数只与脉冲有关系。
反馈清零法
第一种方法是反馈清零:
这里实现的方法就是,是几位进制,那就将此二进制数的
IMPORTANT
由于这里的置零是异步置零,也就是只要置零端有效,那么直接将结果置零。
这也就意味着,如果我们要设计一个
这样就会导致
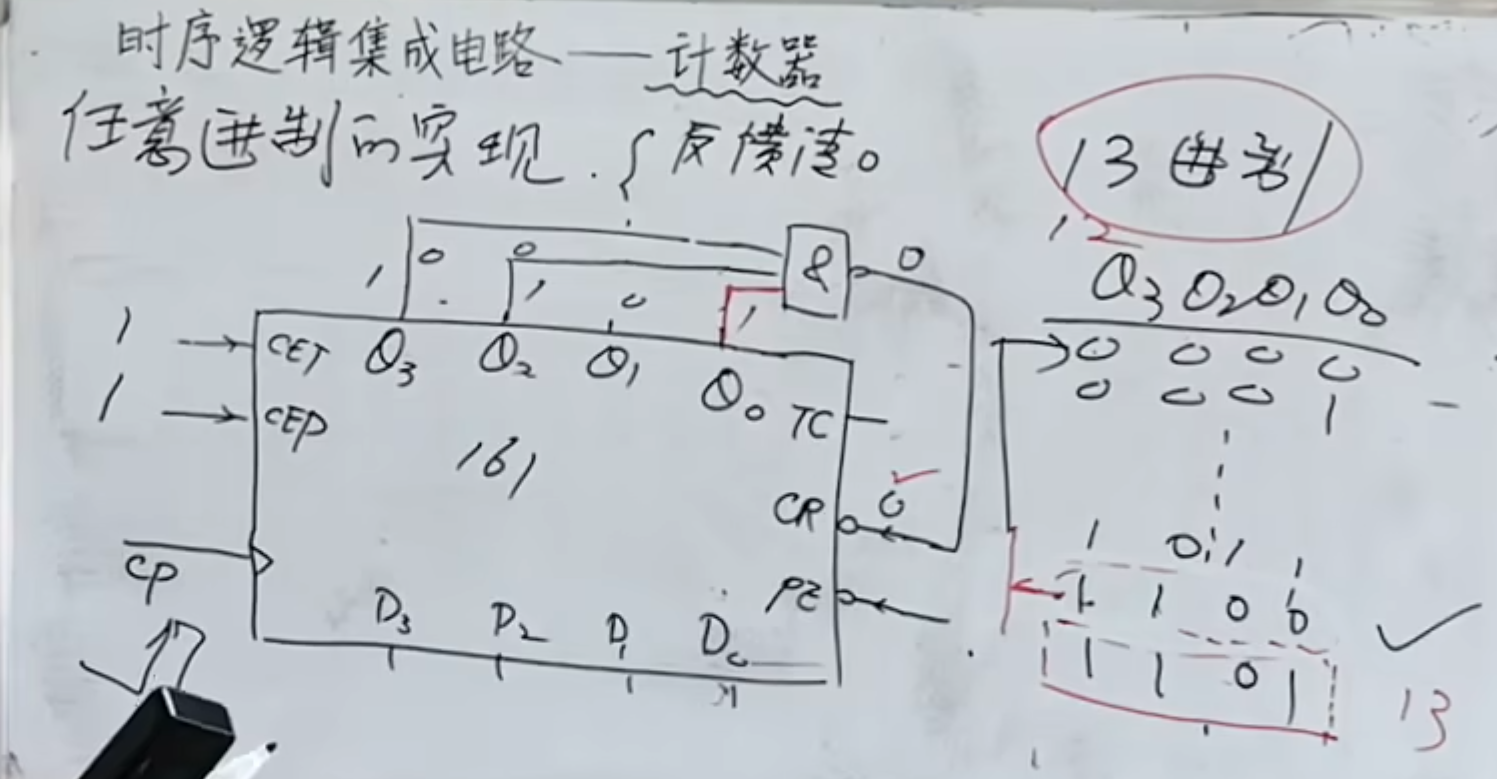
NOTE
清零法一定是从
反馈置数法
第二种方法是反馈置数
反馈置数,运用的就是置数端,而置数端是同步置数(同步置数没有虚位)
当然这里的置数,置的是
然后对于控制置数,则是将第
本质上是因为反馈置数是受
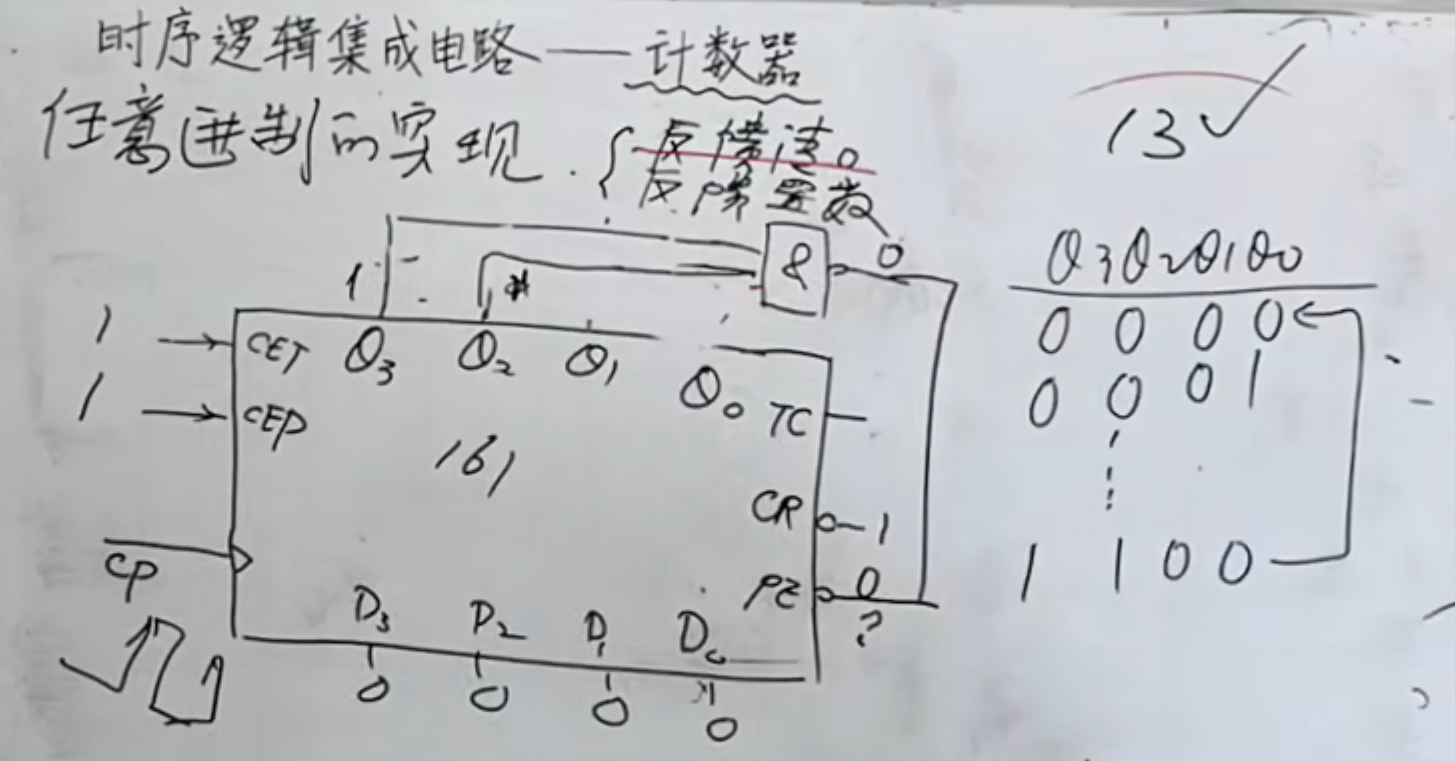
当然,下面的置数不一定非要从

这样就能得到一个公式:
其中,

NOTE
在上面这种情况中,上面的四个输出是

IMPORTANT
只要是在 16 进制以内的,都可以使用一片 161 来实现进制计数器。
但是如果超过 16 进制,那么就需要多片 161 来实现。
任意进制计数器(多片 161)
单片的功能表:

整体反馈法

将两块 161 进行串联,实现
这里需要注意的是右边的是高位,左边的是低位。
只有当低位满
NOTE
当低位的
然后,无论是使用反馈清零法还是反馈置数法都跟一片的时候是一样的。
级联法
NOTE
当要求的进制可以拆成两个数相乘的时候,可以使用级联法,比如:
级联法的核心是将一个多进制的计数器拆成两个小的计数器,例如
NOTE
级联法为了避免过程复杂,一般都使用反馈置数法
首先是用两片分别实现一个
想办法实现当低位计数器达到
所以,要找一个低位满进制之后输出为
连接方法如下图所示(这里是从

而上面多出来的连接到高位与非门上的是为了避免出现高位一到
IMPORTANT
注意,这里并不能将高位改成
160 四位十进制计数器
NOTE
160 与 161 设计上几乎完全一样,唯一的不同在于
当出现

162 十进制和 163 十六进制
NOTE
而

290 二五十异步十进制计数器
基本十进制计数器形式
这个是将一个二进制计数器和一个五进制计数器连接到一起形成一个十进制计数器。
下面这个是第一种连接方法:

以这样的形式实现了十进制计数器
NOTE
这种编码方式是 8421 BCD 码
下面是另外一种连接方法:
这个是把五进制的高位连接到二进制的

NOTE
这个实现的是 5421 BCD 码
集成电路 290 连接方法:

按照上面图中的连接方法就是实现 8421 BCD 编码的十进制计数器
NOTE
上面的
下面这个就是

NOTE
注意,在连接的时候,置零端和置
实现任意进制计数器
实现六进制计数器:

这里与
使用置零端,那就是直接连接
这最后一个(第七个状态)是虚状态。
 王海平
王海平