字数

17006 字

阅读时间

68 分钟

数字电路根据逻辑功能特点分为：组合逻辑电路、时序逻辑电路

NOTE

组合逻辑电路：任一时刻的输出只取决于该时刻的输入信号，而与电路原有的状态无关的电路

时序逻辑电路：任一时刻的输出不仅取决于该时刻的输入信号，而且与电路原有的状态有关的电路

区分组合和时序电路的重要一点是：电路中是否具有触发器

这一章学的是组合逻辑电路。

组合逻辑电路的竞争冒险

产生的原因

看下面这个电路：

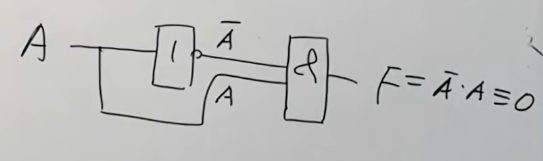
当在静态的时候，很明显，结果为 $A\cdot \bar{A}=0$ ，当然，这个前提就是静态。

但是，当是动态的时候，每个信号进来的时间都是需要时间的。

还是上面这个图，因为上面那条线还经过了一个非门，相比较下面那条线多经过了一个元器件，这样就会出现延迟问题。

分析下来，以 $A$ 信号为例，因为有延迟，就会导致结果偏差：

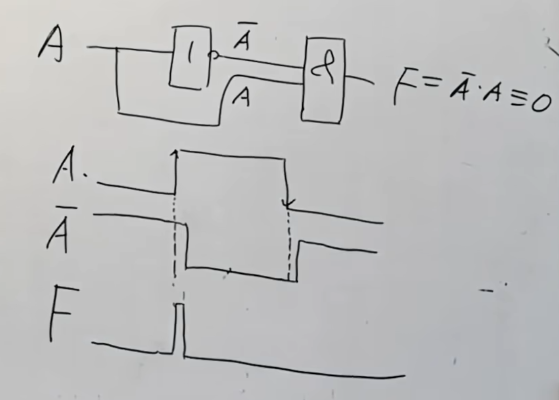
这里就是竞争与冒险，我们把有错误发生的竞争称为冒险

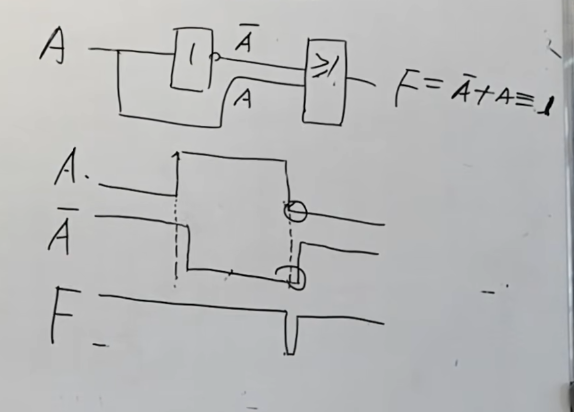
消除方法

改变表达式形式

第一种方法就是改变表达式形式。

避免出现 $A\cdot \bar{A}$ 和 $A+\bar{A}$ 的形式。

例如：

$$F=(A+\bar{B})\cdot (\bar{A}+C)$$

当 $B=1$ ， $C=0$ 的时候，就会出现 $A\cdot \bar{A}$

为了避免竞争冒险，不要使用或与式子

将这个式子展开，就可以得到：

$$F=AC+\bar{A}\cdot \bar{B}+\bar{B}C$$

但其实上面这个也会出现，就是当 $C=1$ ， $B=0$ 的时候，会出现 $A+\bar{A}$ 。但这个时候 $\bar{B}C\equiv 1$ ，那 $A+\bar{A}+1\equiv 1$ ，这也就算是同样避免了这个问题。

人为消除一项（卡诺图）

这个主要是在卡诺图上使用。

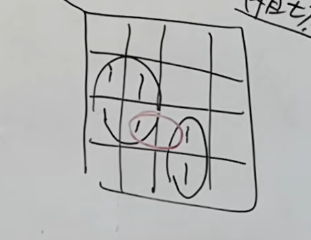
假设函数化简出现下面这种情况。

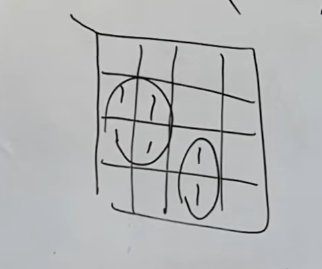
其最简形式就是图上两个圈。但是这样就会出现竞争冒险问题，想要避免此类问题。就是避免圈与圈之间相切

再上图中，就出现了圈与圈相切。解决方法就是用另外一个圈将这两个相切的圈连接起来。如下图所示：

当然，还有下面这种情况：

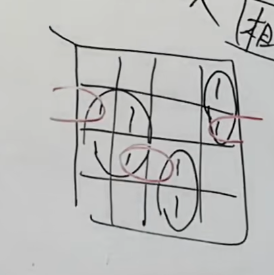
左边的和右边的本质上也是相切的，想要避免竞争冒险，同样的方法就是用另外一个圈将这两个相切的连接起来。

NOTE

主要，如果是函数化简的，那么必须是利用卡托图将其化简到最简形式。

如果是要避免竞争冒险的，那么就需要有几个多余的“圈”。

在输出端接电容

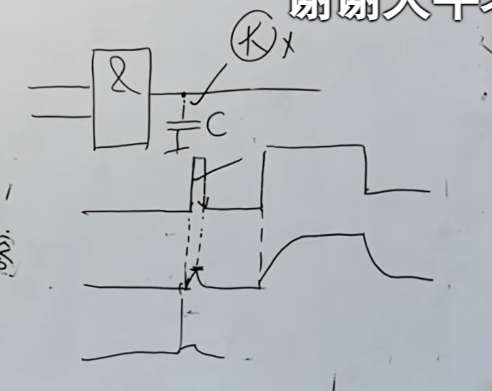
当然，添加电容是最后的办法，原因在于添加电容不只是会对冒险问题进行优化，同样的对于正常的信号也会导致“优化”。

所以电容的选择也是需要考虑的。

组合电路的分析与设计

组合逻辑电路的分析

根据给定的逻辑电路，找出输出与输入之间的逻辑关系，从而确定电路的逻辑功能，比如加法器、减法器等等

基本步骤

例一

通过例题来实现理解：

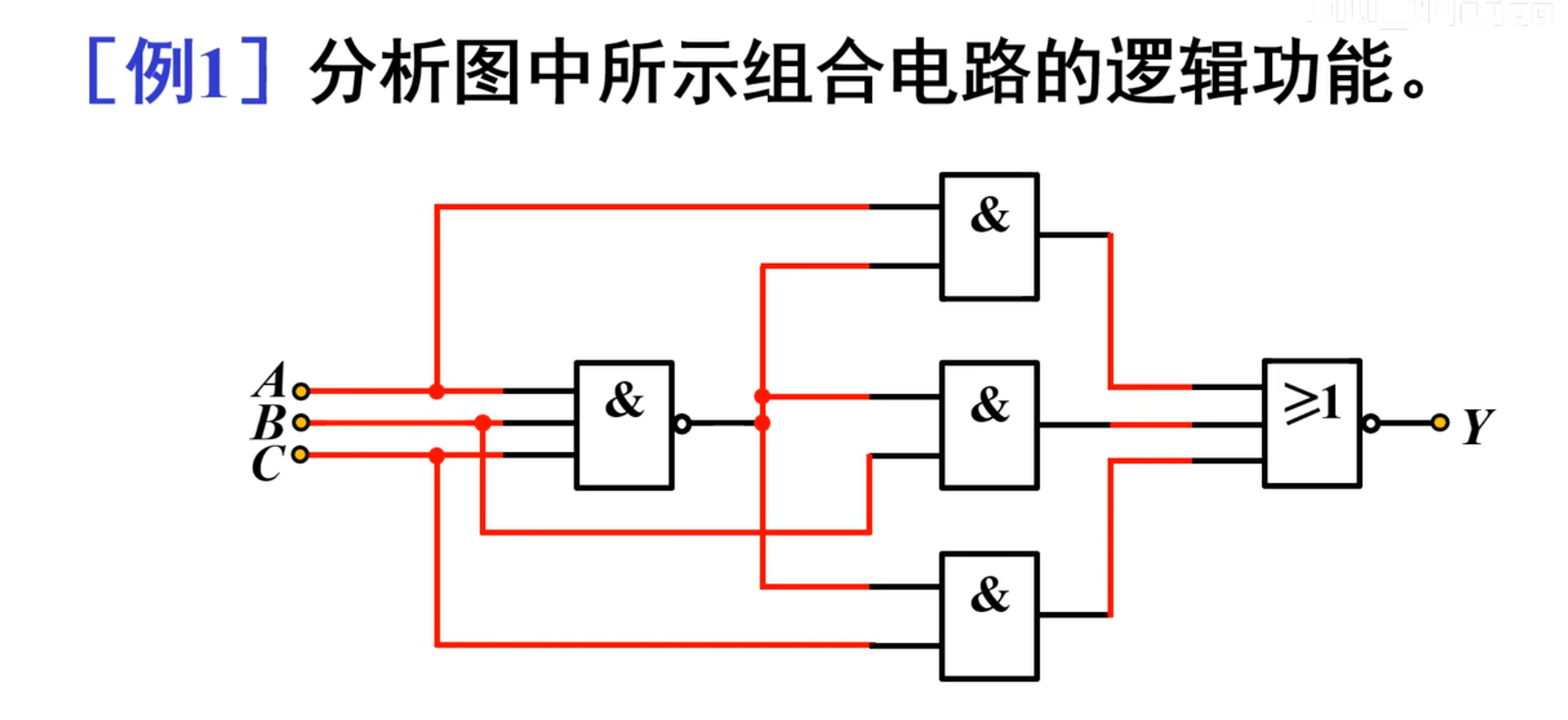
直接计算不方便，所以采用分段计算的方法来求最后的 $Y$ ，将每个门电路后面的输出分别计算出来，最后再进行组合，就是最后的 $Y$

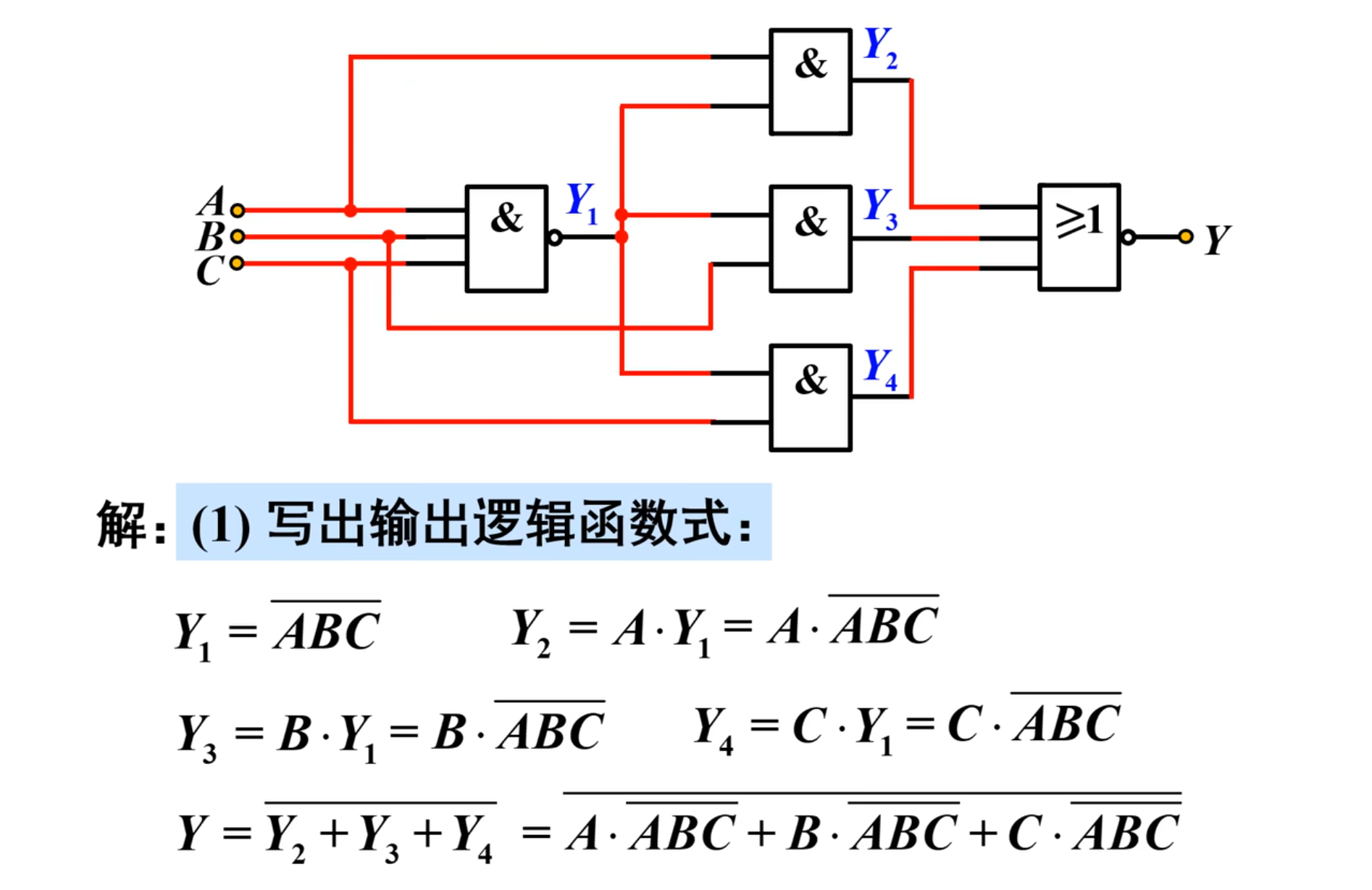
可以得到逻辑函数式：

$$\begin{array}{rl}\mathrm{Y}& =\overline{Y_2+Y_3+Y_4}=\overline{A\cdot \stackrel{―}{ABC}+B\cdot \stackrel{―}{ABC}+C\cdot \stackrel{―}{ABC}}\\ & =\overline{\stackrel{―}{ABC}\cdot (A+B+C)}\\ & =ABC+\overline{A+B+C}\\ & =ABC+\bar{A}\bar{B}\bar{C}\end{array}$$

下面开始列真值表

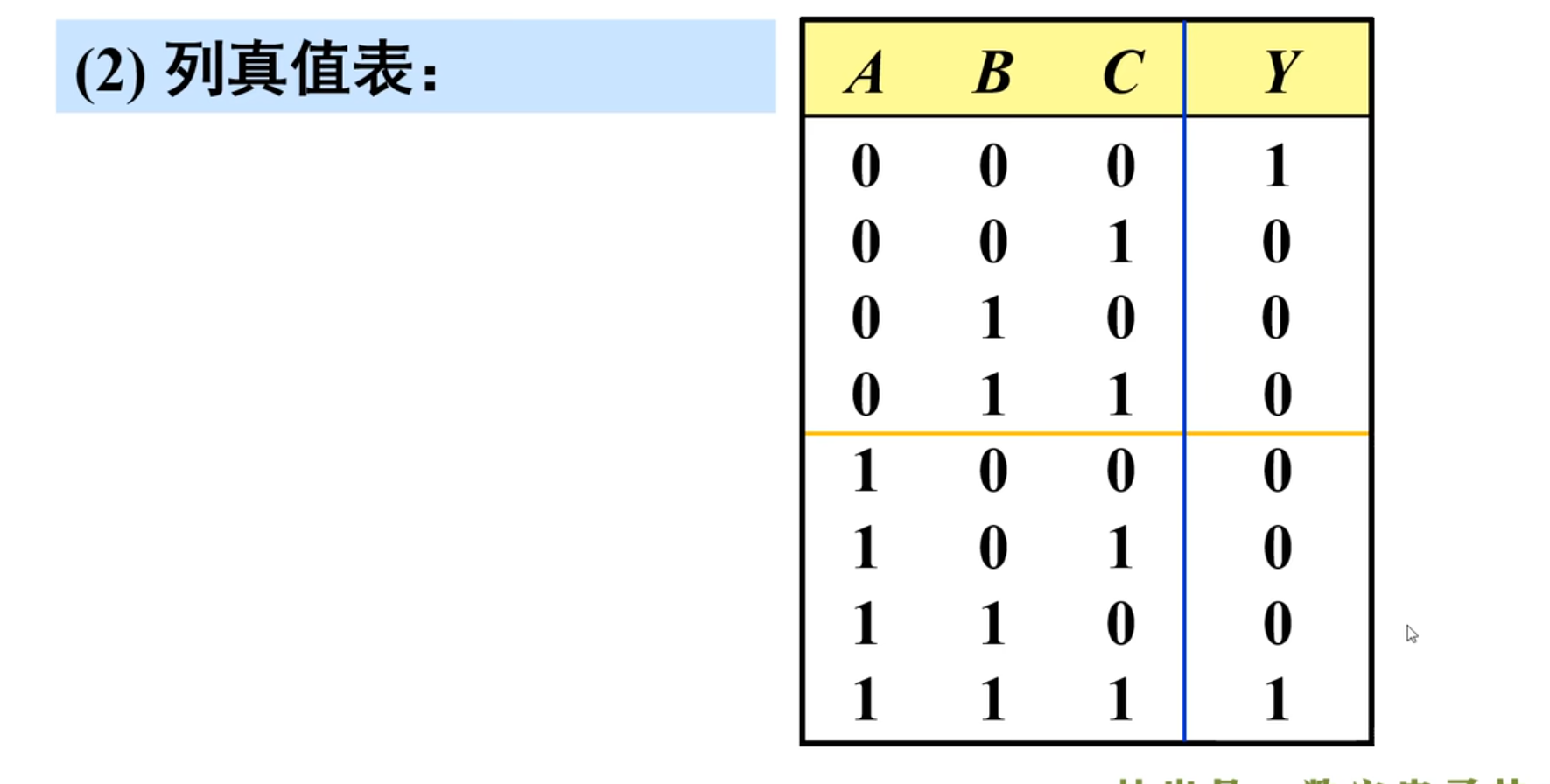
然后是分析逻辑功能

很明显，根据真值表，当 $A$ 、 $B$ 、 $C$ 三个输入变量取值一致的时候（全为 0 或者全为 1），输出 $Y=1$ ，否则为 $0$ 。此电路为一致判断电路

例二

再来一个例题：

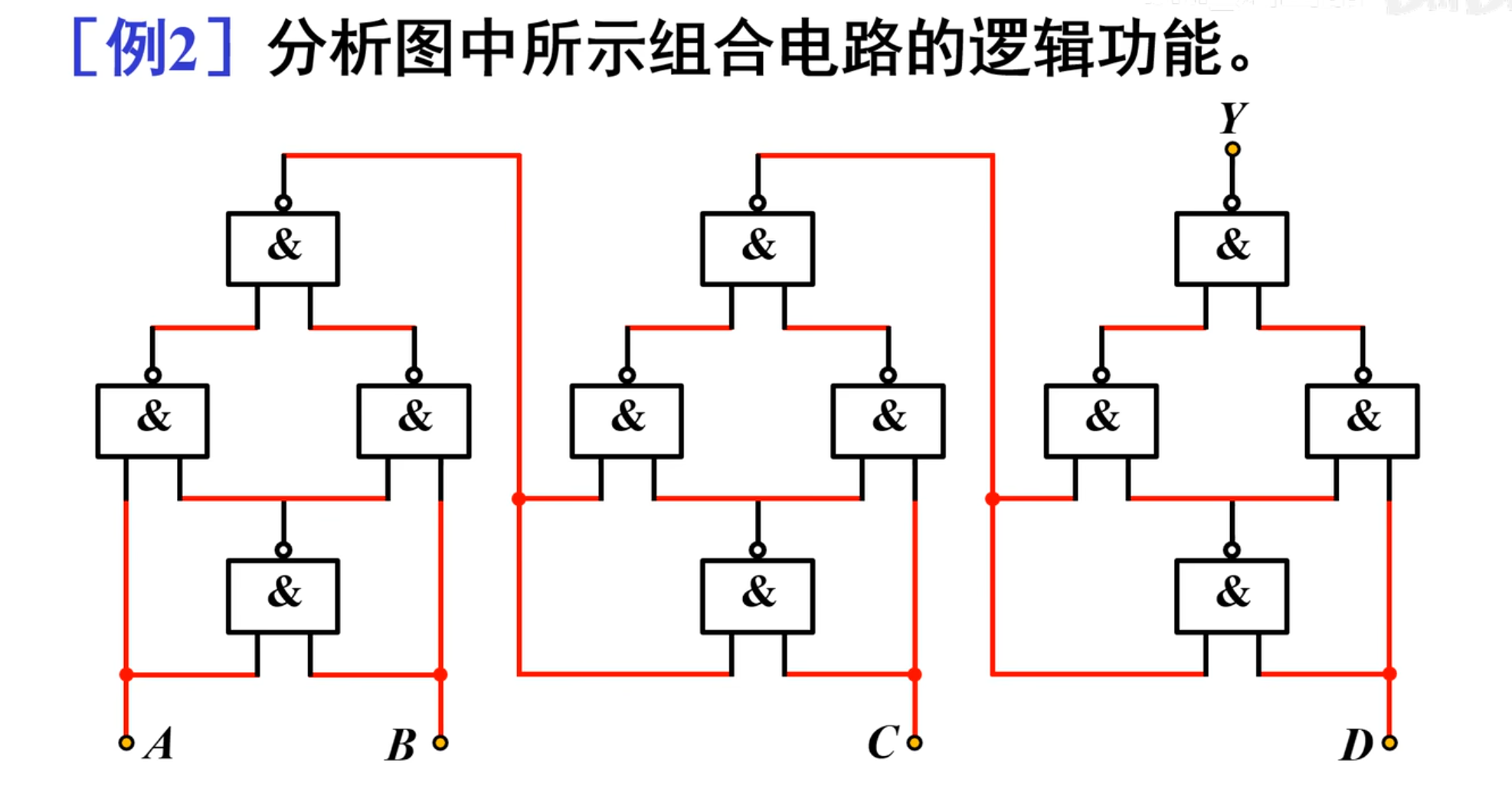
当然了，虽然上面这个图看上去非常复杂，但是不要担心，计算方法还是一样的，首先就是逐级写出逻辑函数式：

先看左边这部分电路：

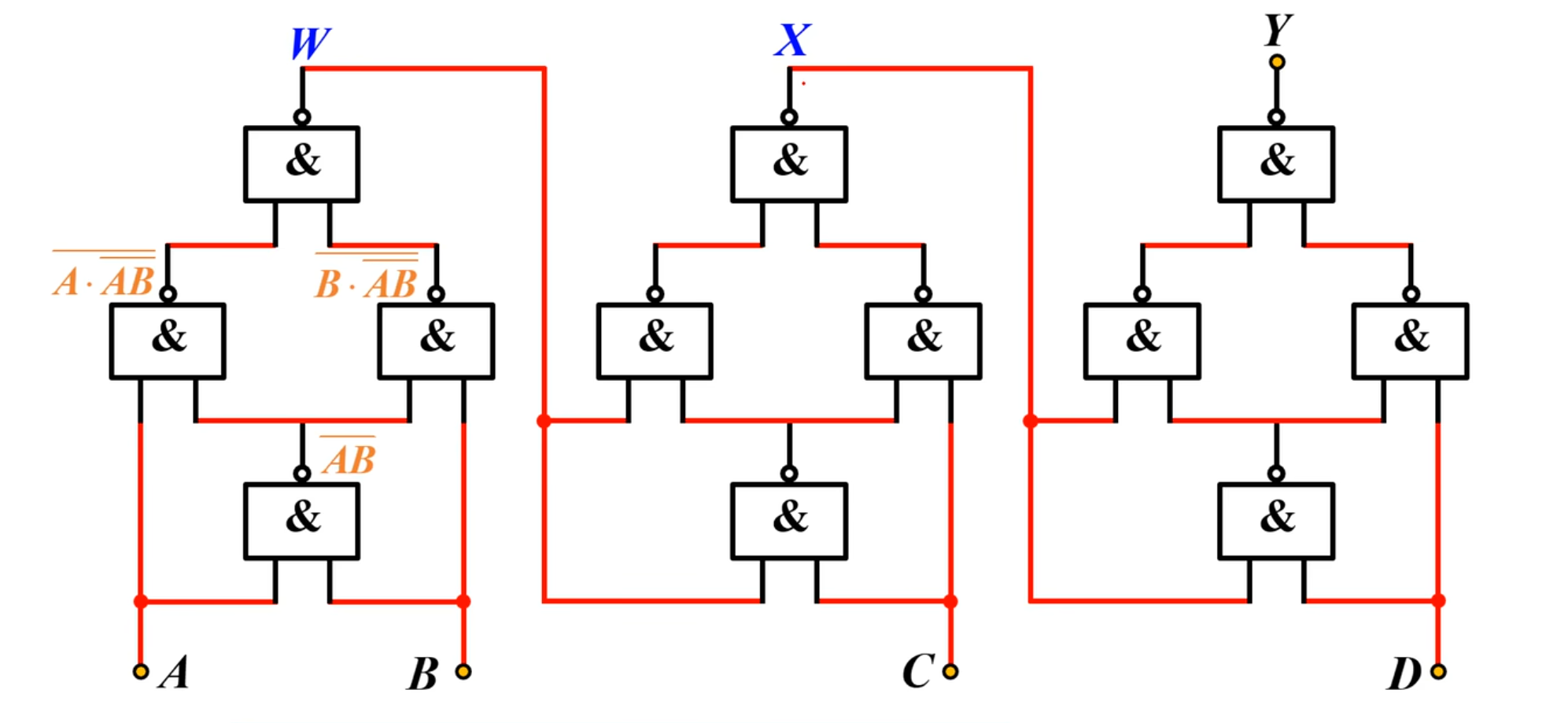
可以得到：

$$\begin{array}{rl}\mathit{W}& =\overline{\stackrel{―}{A\cdot \stackrel{―}{AB}}\cdot \stackrel{―}{B\cdot \stackrel{―}{AB}}}=A\cdot \overline{AB}+B\cdot \overline{AB}\\ & =A\cdot (\bar{A}+\bar{B})+B\cdot (\bar{A}+\bar{B})=A\bar{B}+\bar{A}B=A\oplus B\end{array}$$

通过观察电路结构发现这三部分的电路结构都是一样的。

其实现的功能也是一样的：将两个输入信号进行异或

所以可以直接得到：

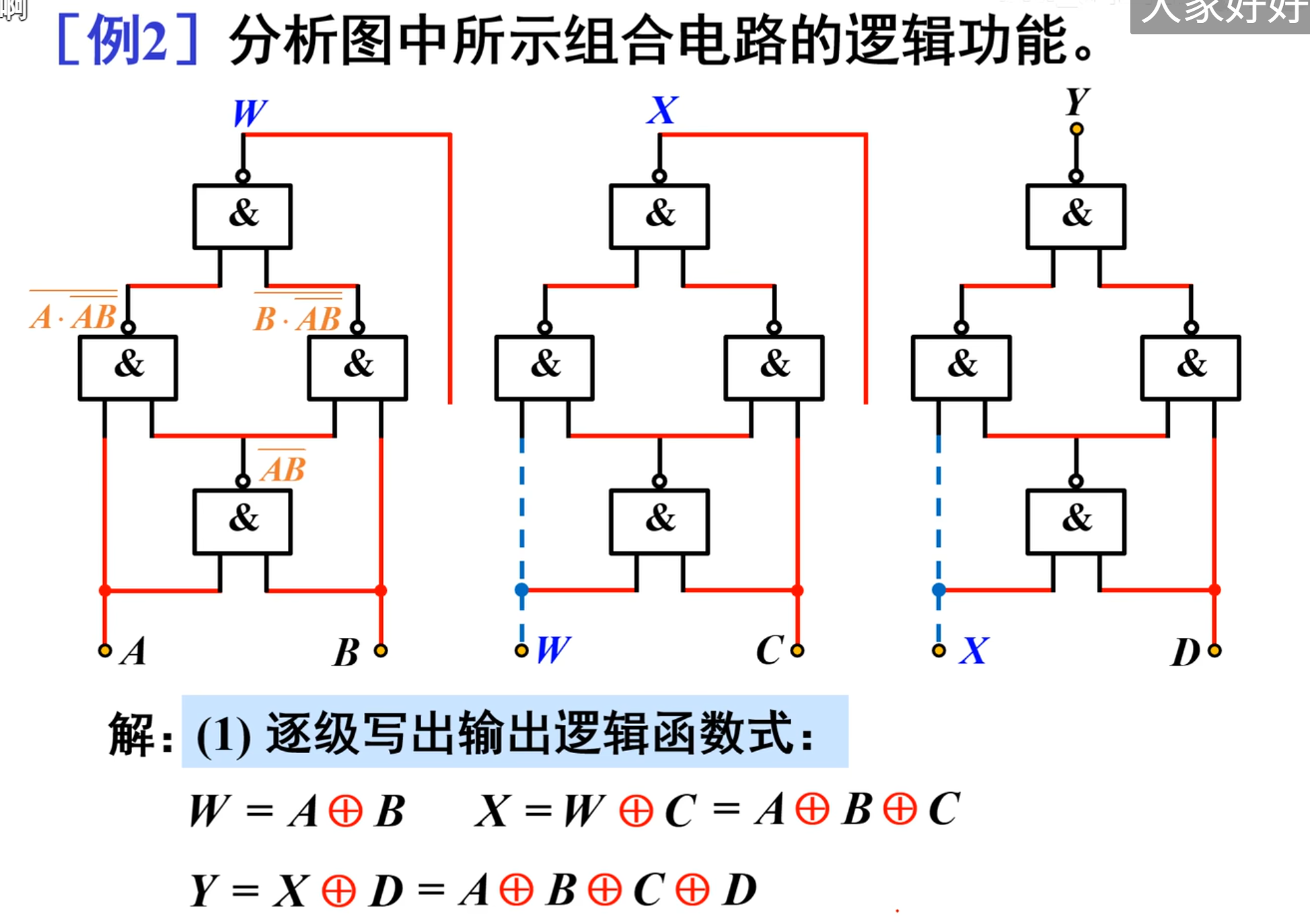
综上所述，我们就得到了最后的结果：

$$Y=A\oplus B\oplus C\oplus D$$

然后，下面来写出真值表。

NOTE

异或的运算规则是：**相同为 $0$ ，不同为 $1$ **

同时，在这里补充一个：

奇数个 1 进行异或，结果为 1

偶数个 1 进行异或，结果为 0

慢慢计算之后得到的结果是：

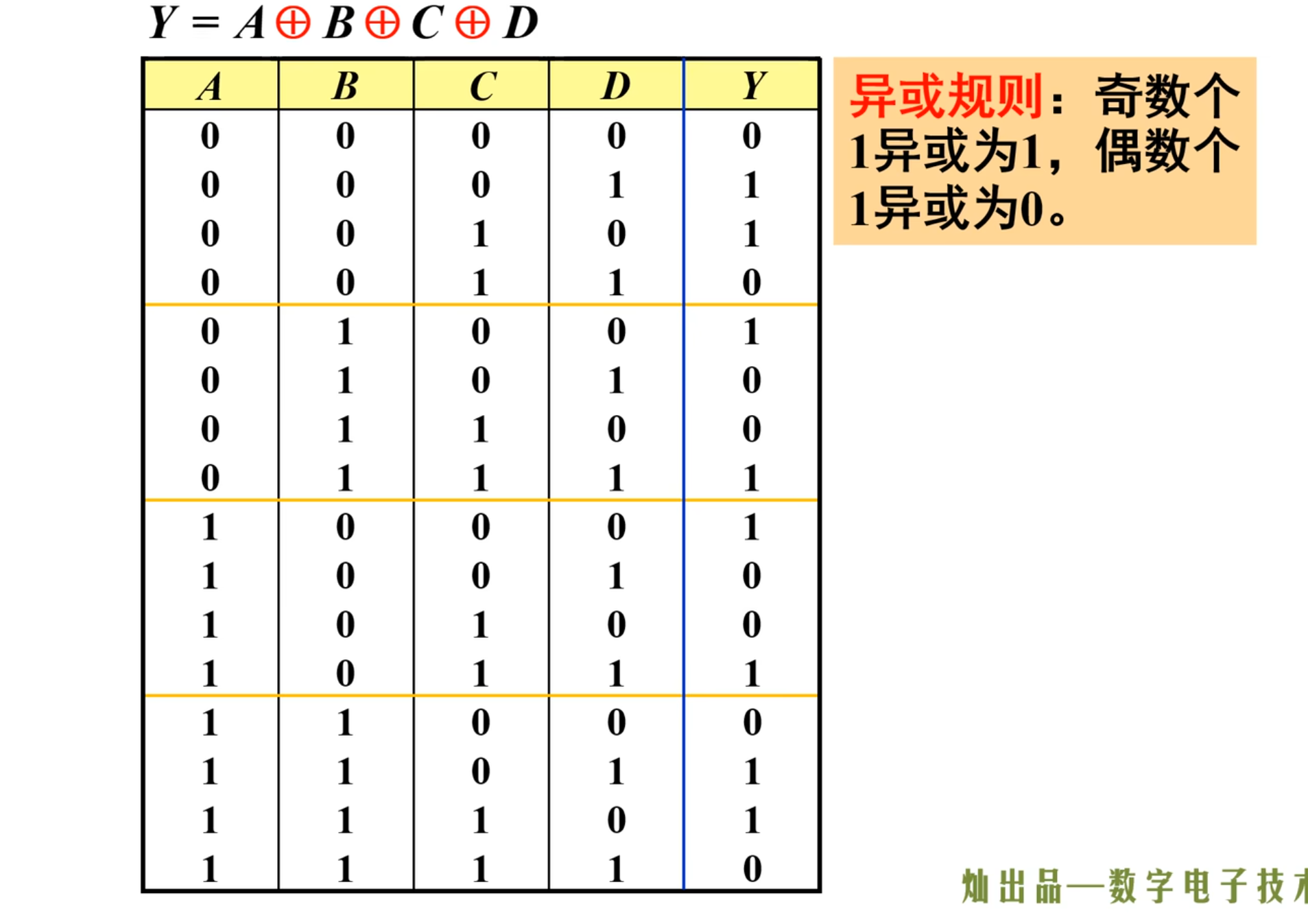
然是进行功能说明：

通过观察真值表，可以得到：当 4 个输入变量中，1 的个数为奇数的时，输出为 1，当 1 的个数为偶数时，输出为 0，所以判断电路为检奇电路

组合逻辑电路的设计

基本设计步骤：

设计思路：分析给定的逻辑要求，设计出能够实现该功能的组合逻辑电路。

基本步骤：

其中的逻辑抽象是需要额外注意的地方。

IMPORTANT

首先是分析给定问题，确定输入变量和输出变量，并进行状态赋值（什么时候取值 0，什么时候取值 1），然后分析输出变量和输入变量之间的逻辑关系，列出真值表。

得到真值表之后，使用代数法或者卡诺图法来求最简与或式

然后根据题目中要求的门电路，将最简与或式变换成要求门类型对应的最简式。

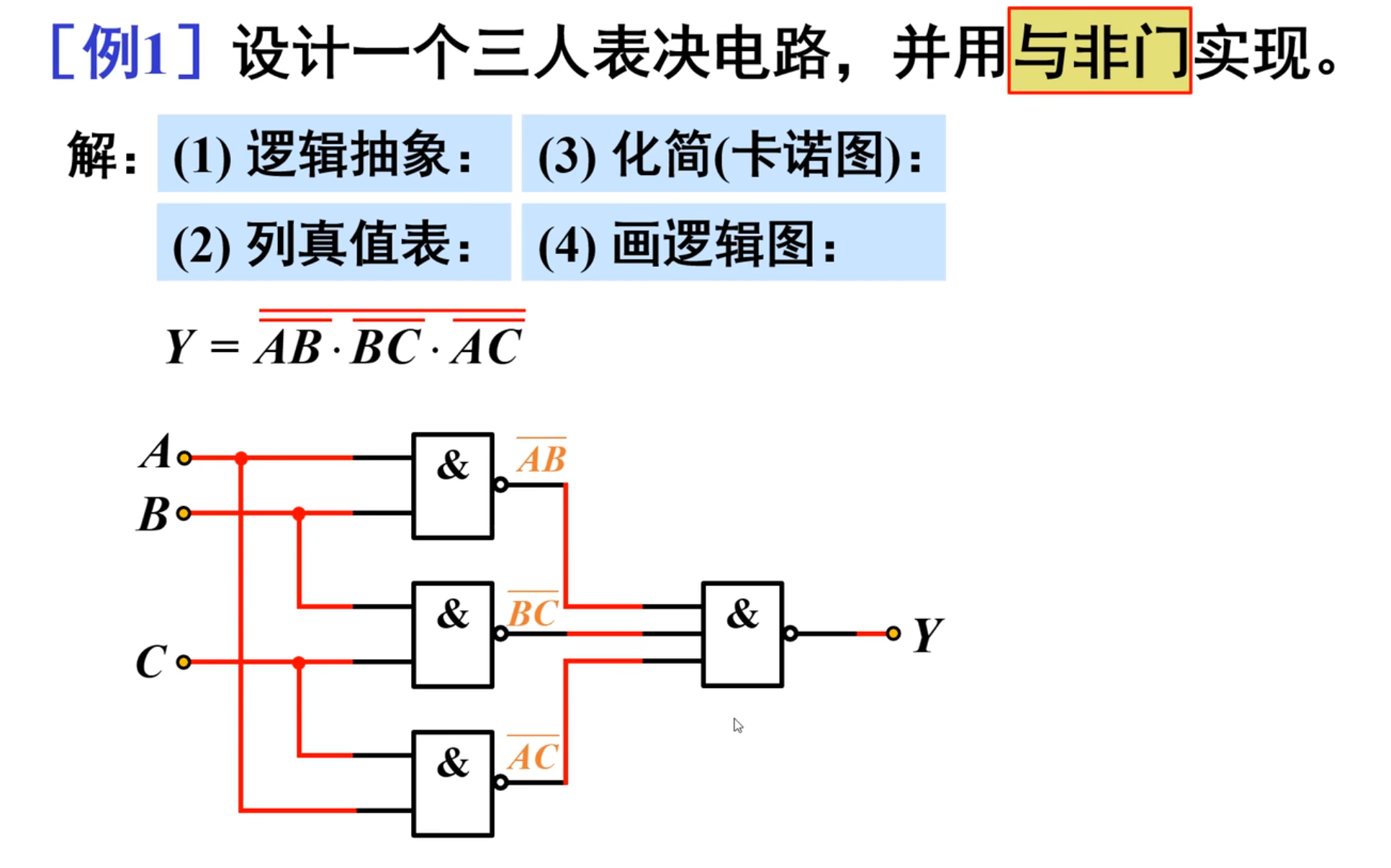
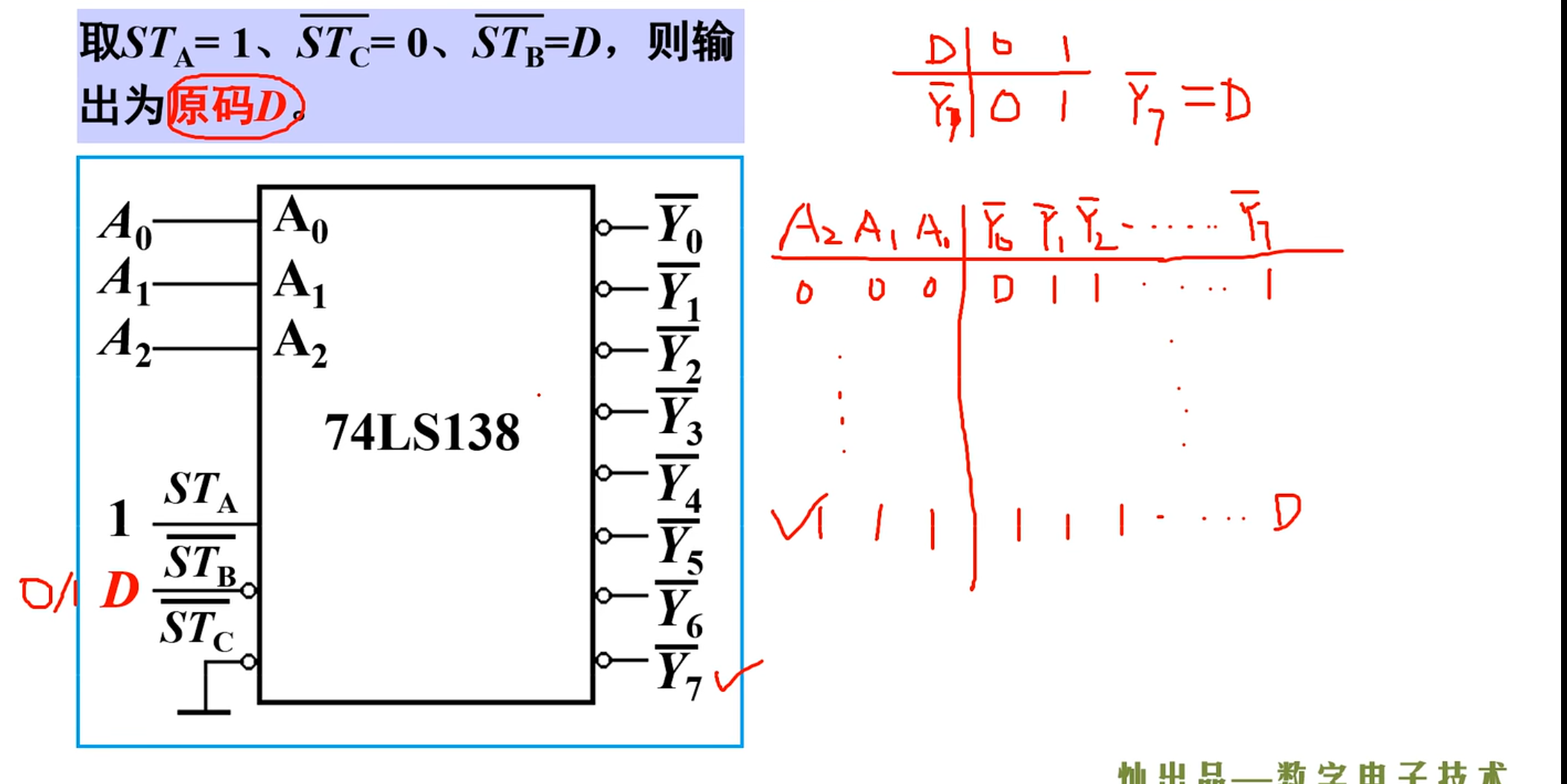
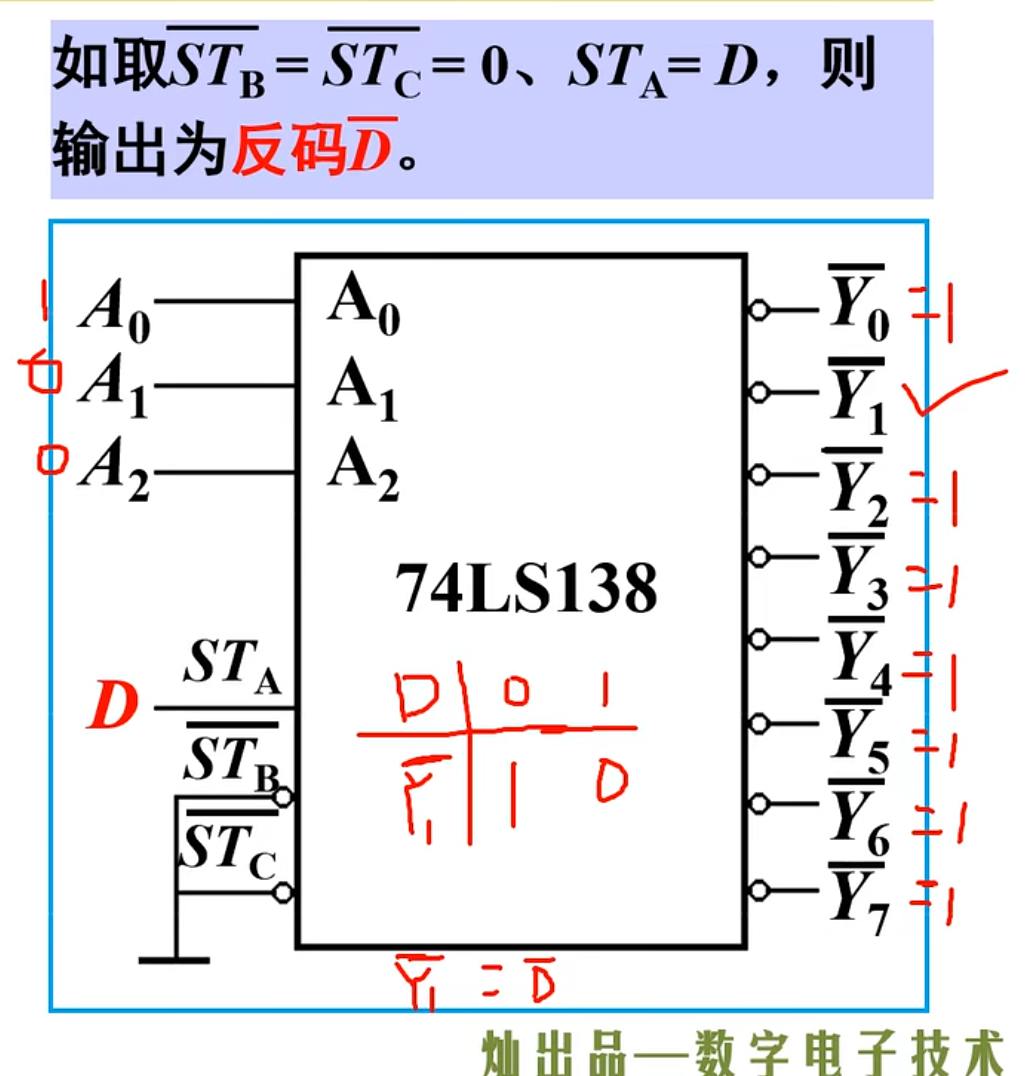
例一 - 三人表决器

直接根据例题：

首先是将逻辑抽象。

设定变量：有三个人，所以要有三个变量输入，同时输出为 $Y$

然后进行状态赋值。

因为要设计一个表决器，那就有两种状态，一种是赞同，一种是不赞同。结果也有两种，一种是通过，一种是不通过。

当然，在这个题目中，其实说明的不是很具体，应该是有三分之二的人表示同意，则表决通过，反之，不通过。满足少数服从多数。

下面来列出真值表。

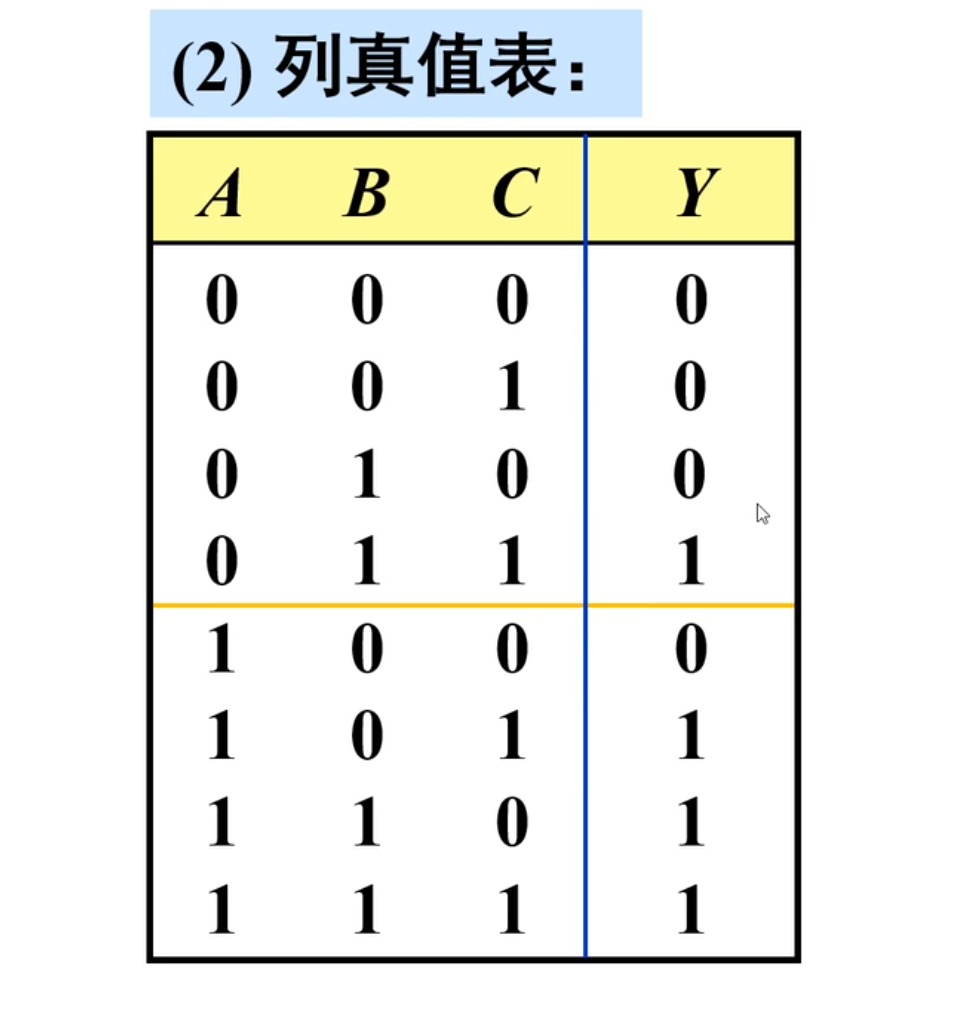
下面进行化简真值表，其中最好的方法其实就是卡诺图。（注意用循环码的方法来画卡诺图）

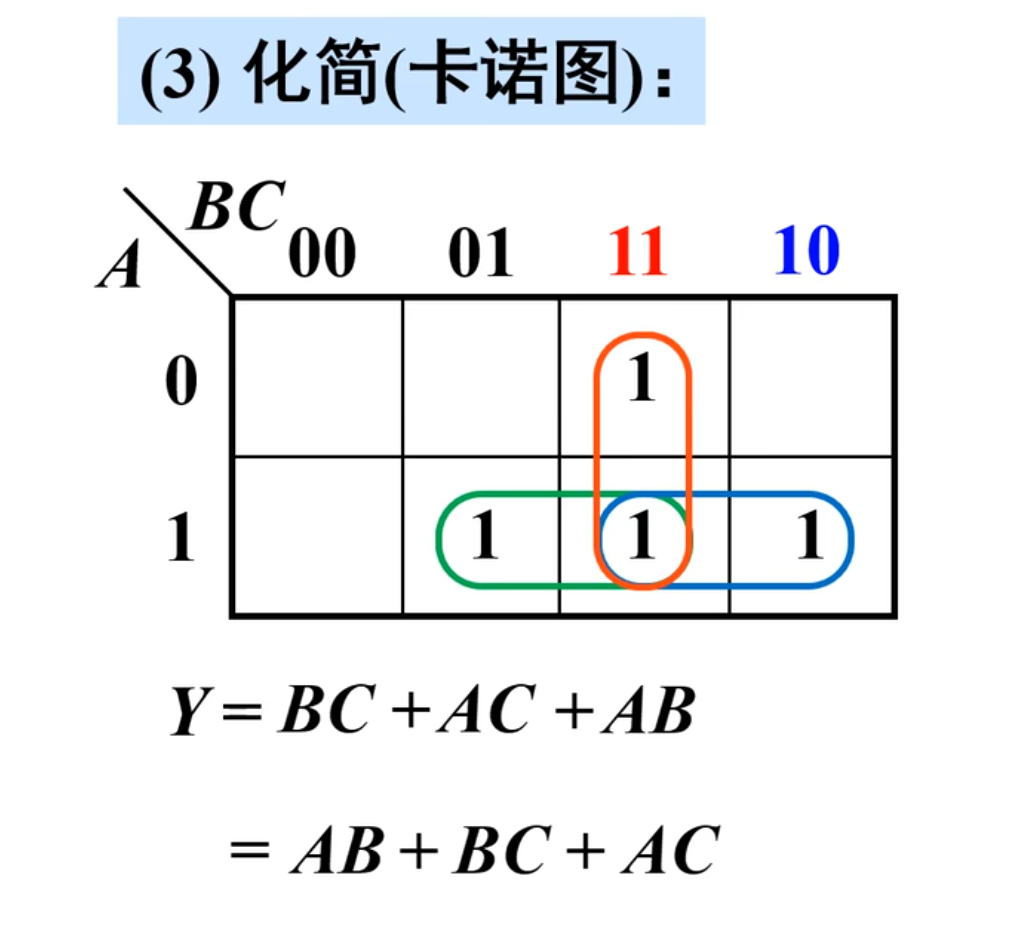
得到最简与或式之后，还要分析题目中的要求，题目中要求用与非门来实现这个电路

所以要对卡诺图化简得到的结果进行变换。

NOTE

求与非门的一个技巧是对原与或式进行两次取反。

$$\begin{array}{rl}Y& =BC+AC+AB\\ & =\overline{\stackrel{―}{AB+BC+AC}}\\ & =\overline{\stackrel{―}{AB}\cdot \stackrel{―}{BC}\cdot \stackrel{―}{AC}}\end{array}$$

最后就是来画电路逻辑图了。

例二 - 四位二进制转格雷码

再来一个例题：

还是按照步骤，首先是进行逻辑抽象，先设定变量：

四位二进制代码用 $A_3$ 、 $A_2$ 、 $A_1$ 、 $A_0$ 来表示。输出格雷码用 $Y_3$ 、 $Y_2$ 、 $Y_1$ 、 $Y_0$ 来表示。

NOTE

格雷码：两个相邻码之间只有一位不同

那如何实现将二进制码转换为格雷码呢？

有两种方法：

1. 第一个是使用公式法： $G_i=B_{i+1}\oplus B_i$

   

2. 用卡诺图

   

   这个方法最主要的是需要知道其循环的顺序，这个顺序就是最后的真值表的结果。

下面开始列真值表：

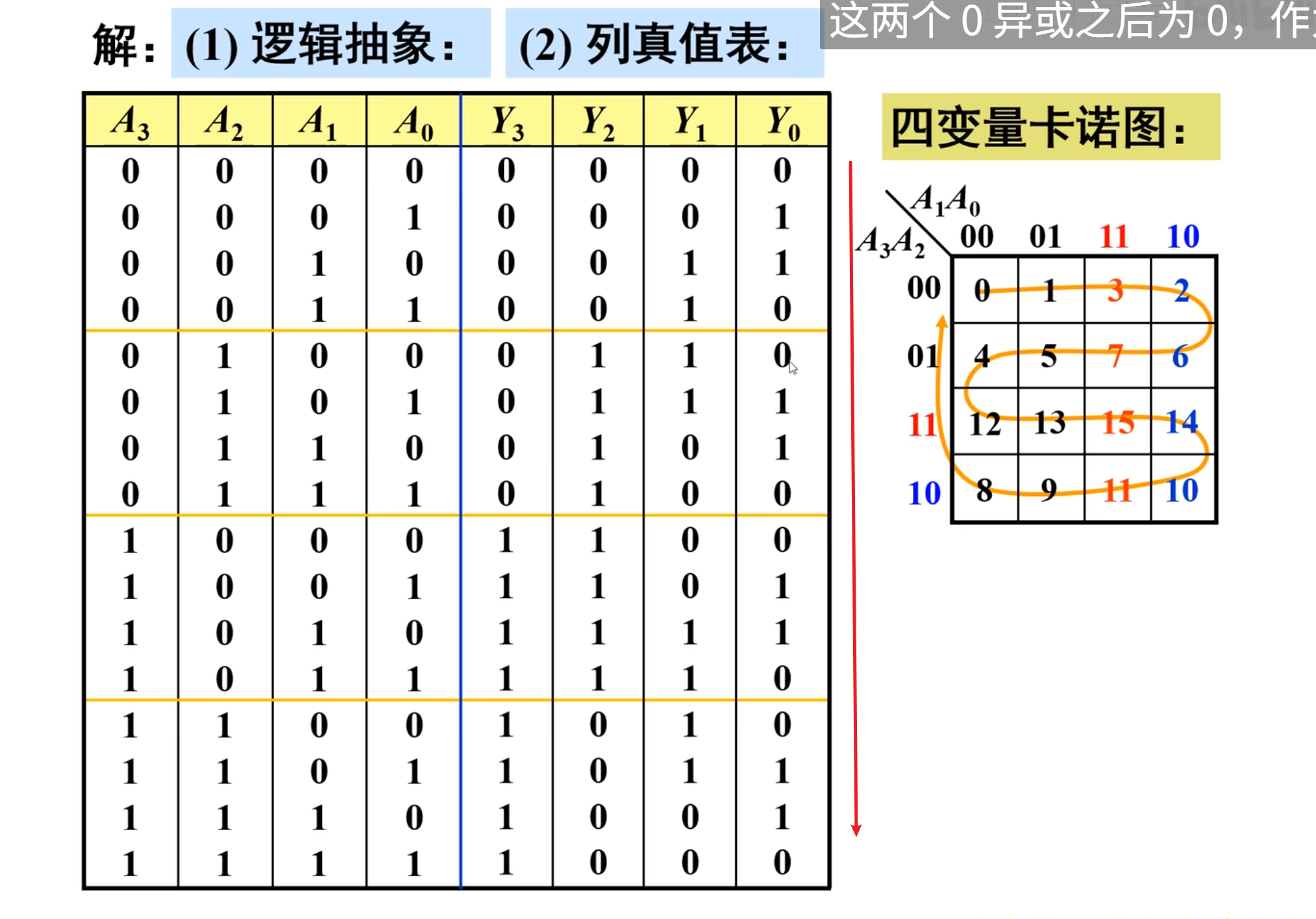
按照右边卡诺图上的顺序在左边的输出上依次写出来就是最后的答案。

下面根据上面的真值表来使用卡诺图进行化简

当然，尽管上面的真值表中是四个输出，只需要将这四个输出拆开即可。

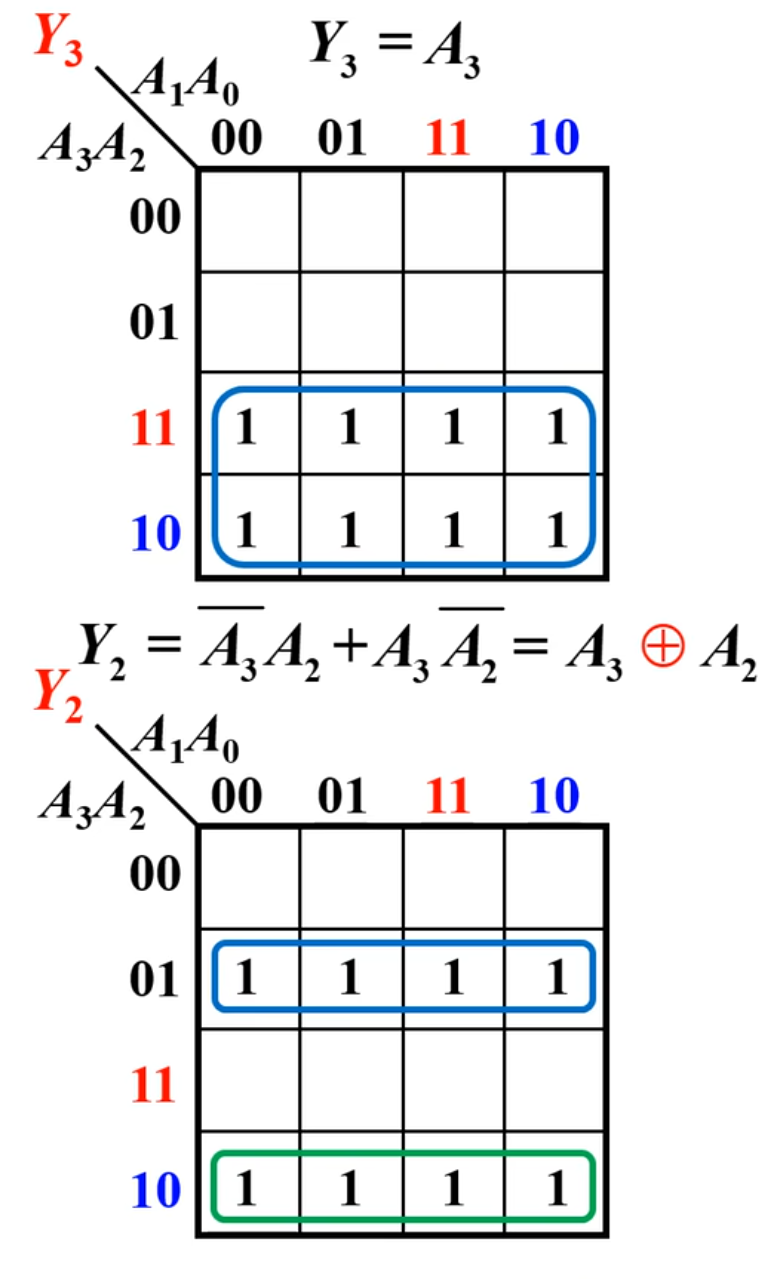
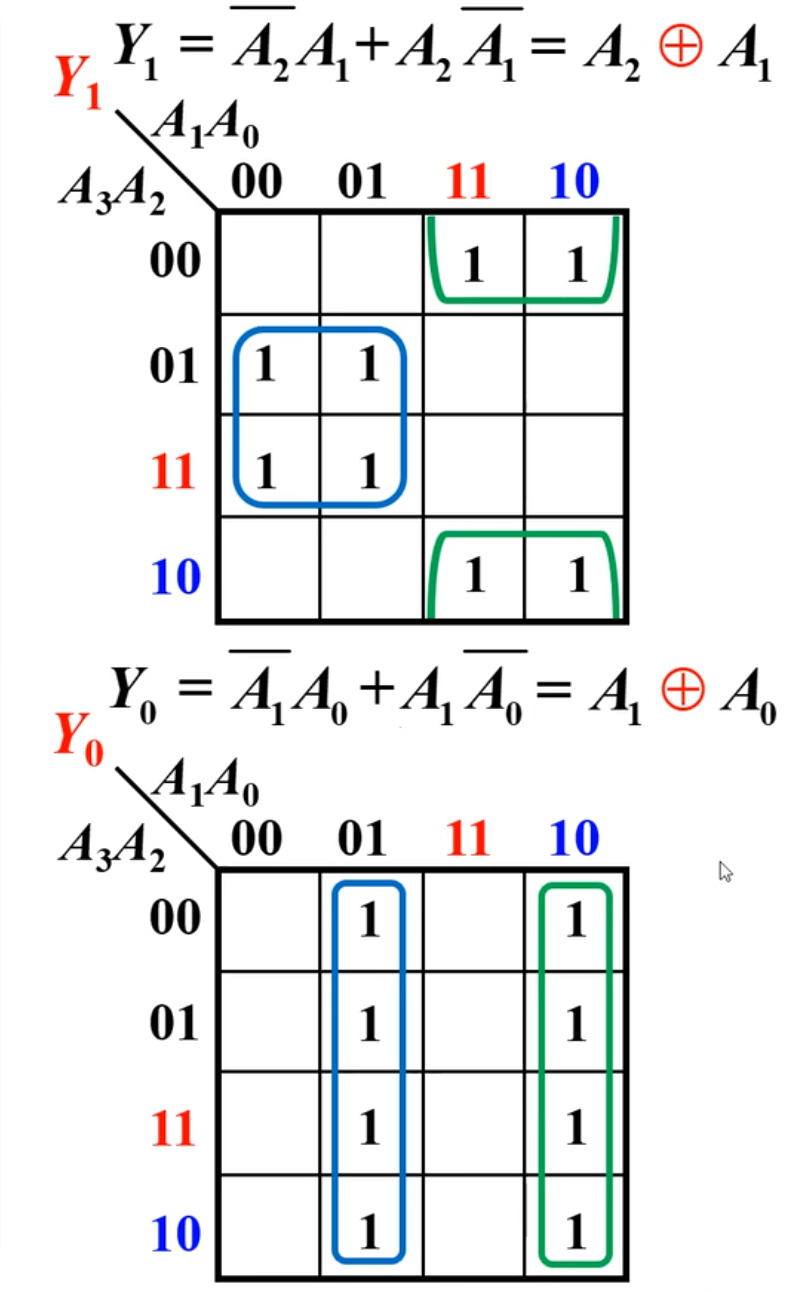
根据上面的化简，得到的结果是：

$Y_3=A_3$ ， $Y_2=A_3\oplus A_2$ ， $Y_1=A_2\oplus A_1$ ， $Y_0=A_1\oplus A_0$

然后来画电路逻辑图

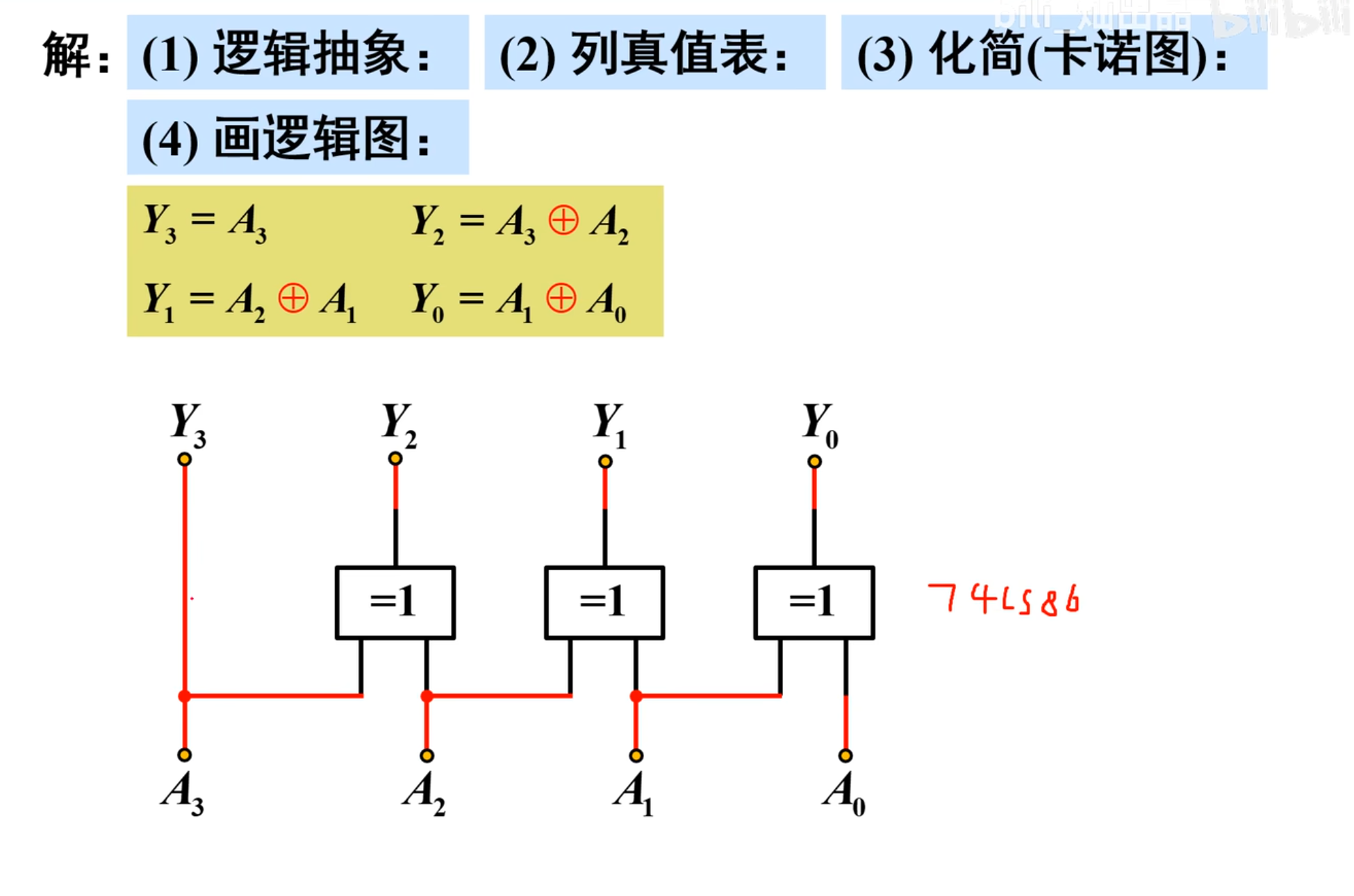
算数运算电路 - 加法器和数值比较器

数字系统中除了进行逻辑运算之外，还经常需要进行数值的算术运算，而在系统中的加、减、乘、除都是利用加法器来进行的，所以加法器便成为了数字系统中最基本的运算单元。

半加器

两个 $1$ 位的二进制数相加，不考虑低位进位的加法。（注意，这里还是有高位进位的，当作一个输出，只是不考虑低位进位。）

实现半加功能的电路称为半加器。

NOTE

半加的规则：两个 1 位二进制数想加，结果有 2 个输出：半加和 $S$ （本位和）、半加进位 $C$

所以，根据上面描述，得到真值表：

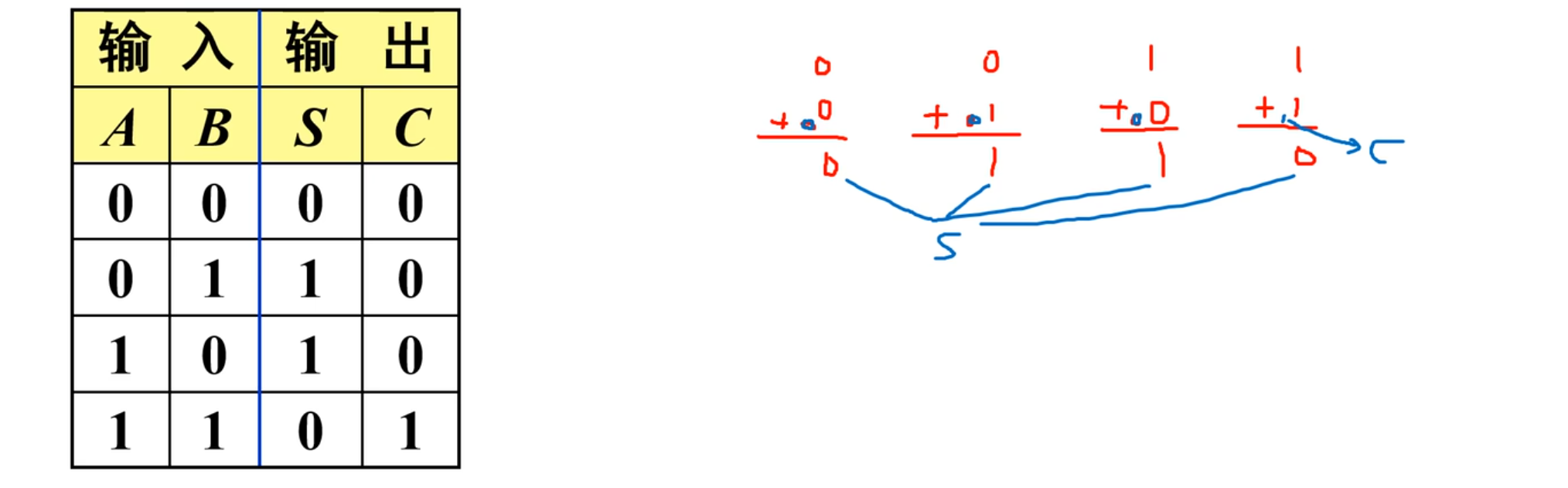
很明显，根据真值表，可以得到：

$$[\begin{array}{rl}S& =A\bar{B}+\bar{A}B=A\oplus B\\ C& =AB\end{array}$$

然后来画电路逻辑图：

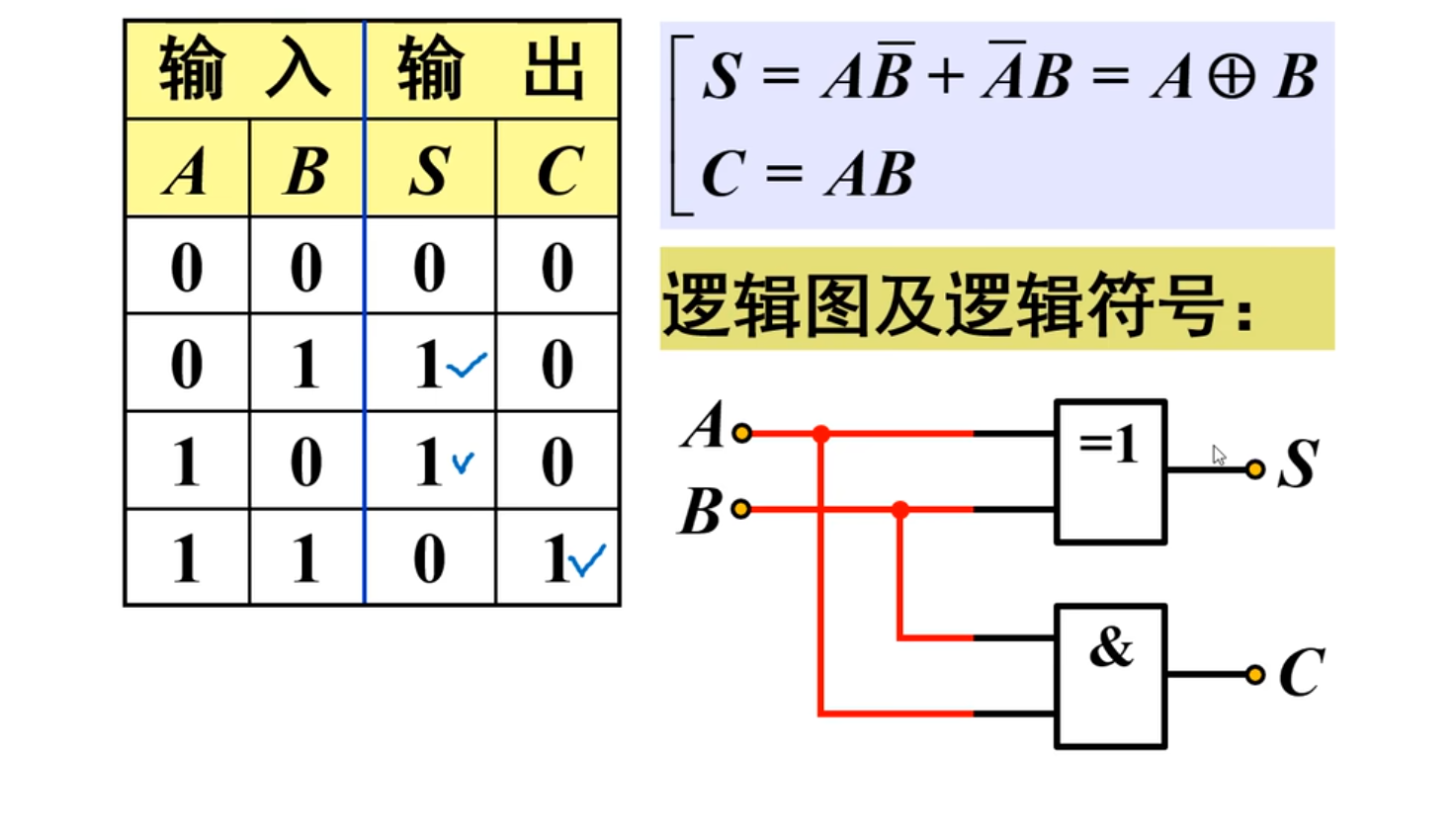
当然，在一些电路中，可以将上面这个半加器化简成一个符号来表示：

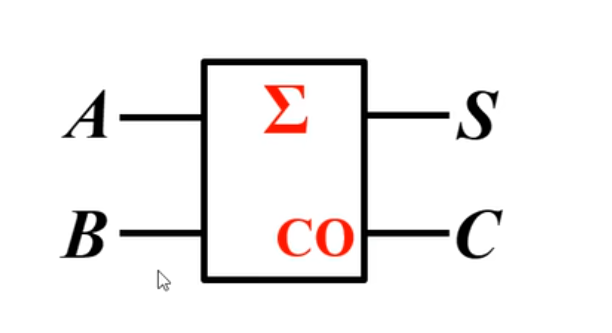
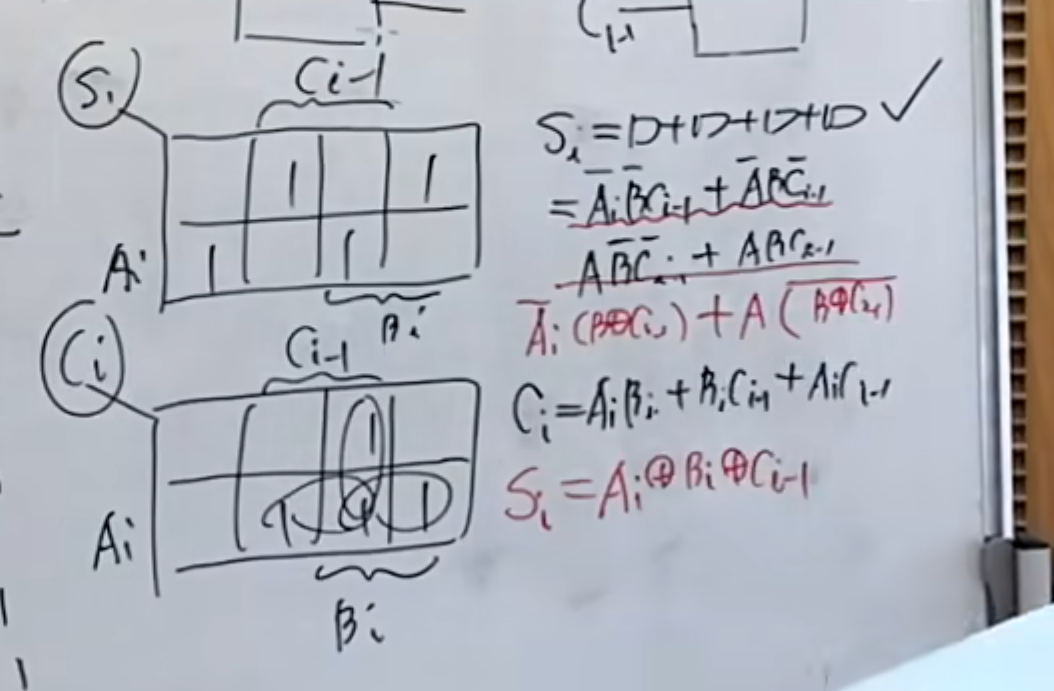
全加器

将本位的 2 个二进制数和相邻低位来的进位数进行相加的加法。

实现全加功能的电路称为全加器。

NOTE

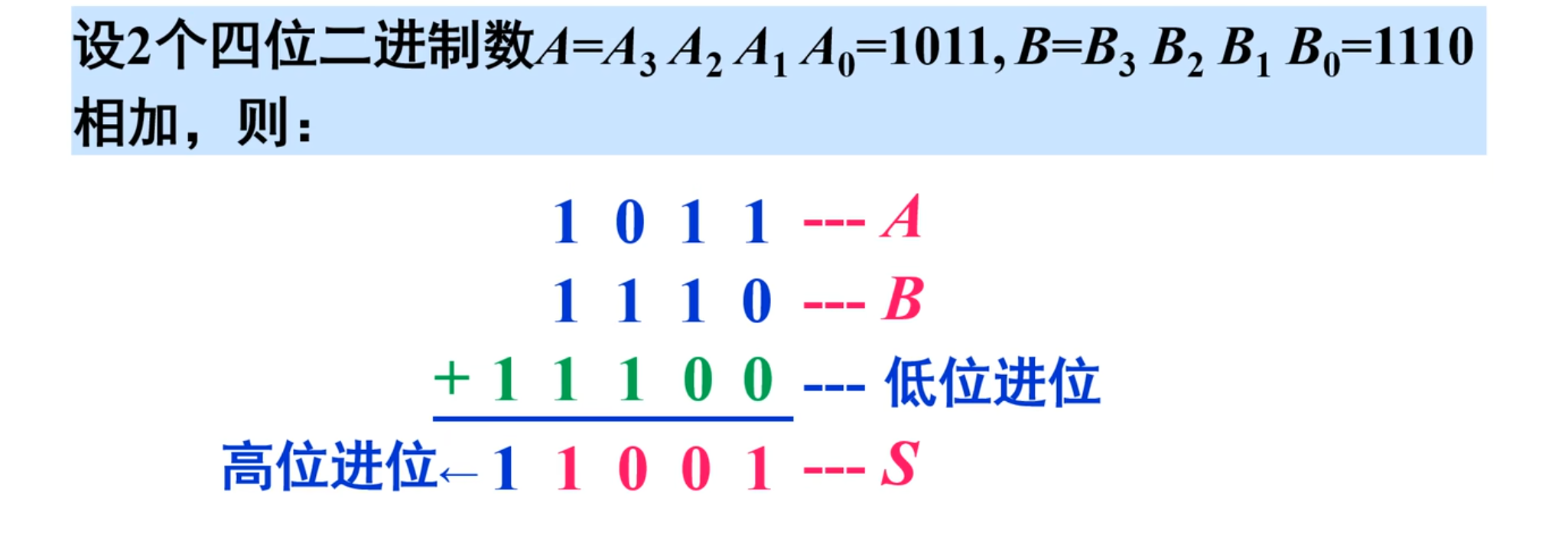
这里需要注意，虽然看上去是两个二进制数在进行相加，但是还隐藏了一个低位进位的输入，所以在真值表上其实是有三个输入。

IMPORTANT

$A_i,B_i$ 表示 $A$ 、 $B\mathbf{\text{两 个 数 中 的 第 }}i$ 位， $C_i-1\mathbf{\text{表 }}$ 示来自低位 (第 $i-1$ 位) 的进位， $S_i$ 表示全加和， $C_i$ 表示送给高位 (第 $i+1$ 位) 的进位。

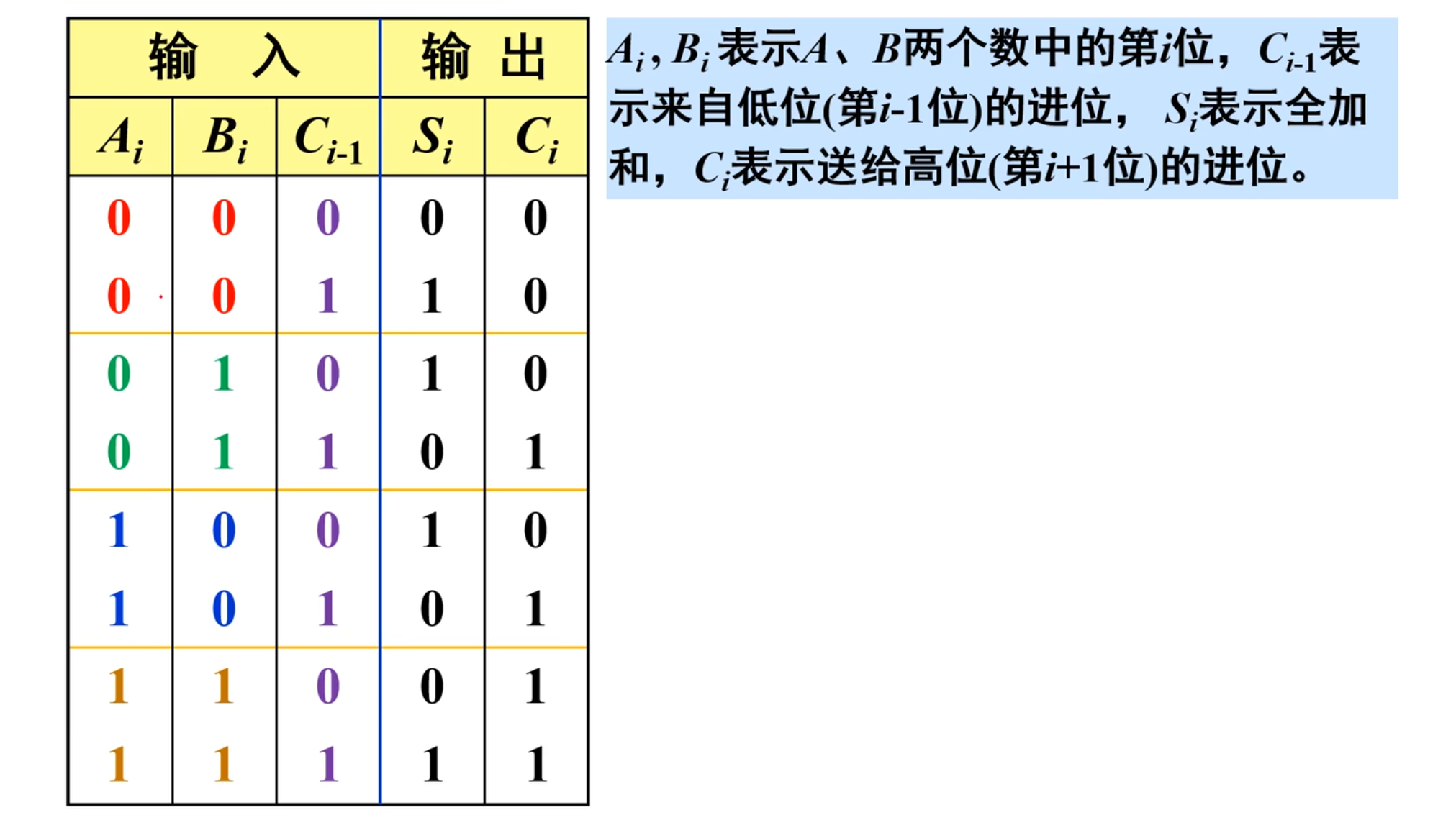
注意看，上面真值表中的第三个输入代表是否有进位，如果有进位，则需要将进位也计算在内。

后面的输出部分，本质上是把一次运算的结果拆成两部分，一部分（ $S_i$ ）是本位得到的，一部分 $C_i$ 是向上一位送去的。

然后，再仔细观察真值表，发现当三个输入中有奇数个 1 的时候， $S_i$ 为 1，当输入中有偶数个 $1$ 的时候， $S_i$ 为 0

所以根据经验就可以得到：

$$\begin{array}{rl}{S}_i& =\overline{A_i}\cdot \overline{B_i}{C}_{i-1}+\overline{A_i}{B}_i\overline{C_{i-1}}+A_i\overline{B_i}\cdot \overline{C_i}+A_i{B}_i\cdot \overline{C_{i-1}}\\ & =\overline{A_i}(B_i\oplus C_{i-1})+A\cdot \overline{(B_i+C_{i-1})}\\ & =A_i\oplus B_i\oplus C_{i-1}\end{array}$$

当然也可以用卡诺图的方法计算出来，其结果是一样的。

$C_i$ 同样可以使用卡诺图的方法得到：

$$\begin{array}{rl}{C}_i& =A_i{B}_i\overline{C_i}+A_i\overline{B_i}{C}_{i-1}+\overline{A_i}{B}_i{C}_{i-1}+A_i{B}_i{C}_i\\ & =(A_i\oplus B_i)C_{i-1}+A_i{B}_i\end{array}$$

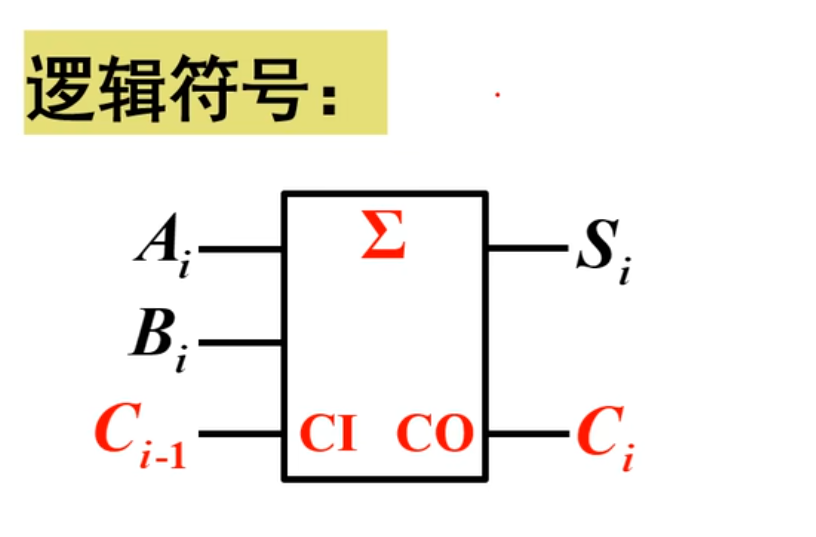
然后其符号如下：

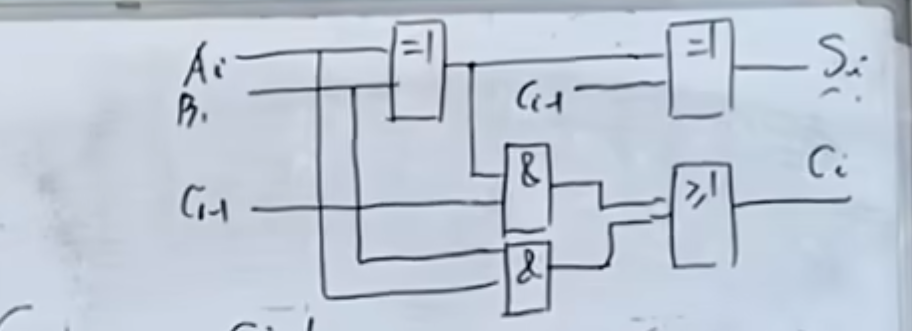
实现全加器的逻辑电路如下：

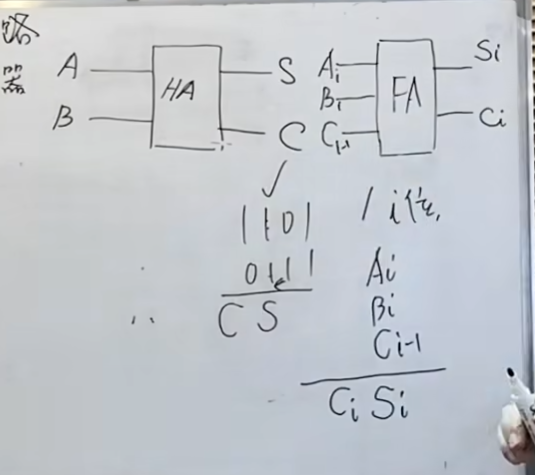
使用半加器实现全加器

主要使用的是半加器的性质，两个输出一个是进位输出（与），一个是本位和（异或）

这样，按照功能其实就能得到连接方法：

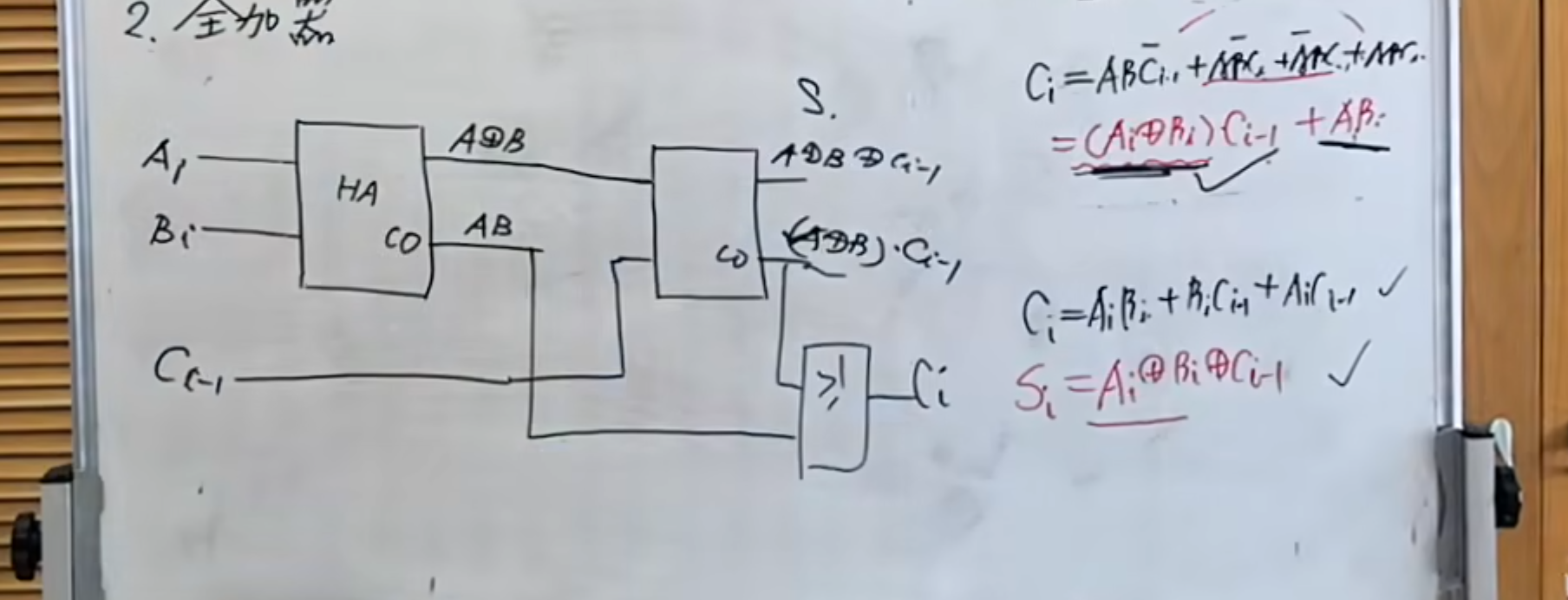
用两个半加器和一个或门就能得到一个全加器。

全加器实现二进制乘法

注意，除了最后一位，其他位上相加都会有进位的存在。

因为在计算中存在进位的问题，所以不能简单的用与或来表示，要用到之前提到的全加器。

注意，全加器有两个输出，分别代表本位输出和进位输出。

综上所述，乘法的电子逻辑图为：

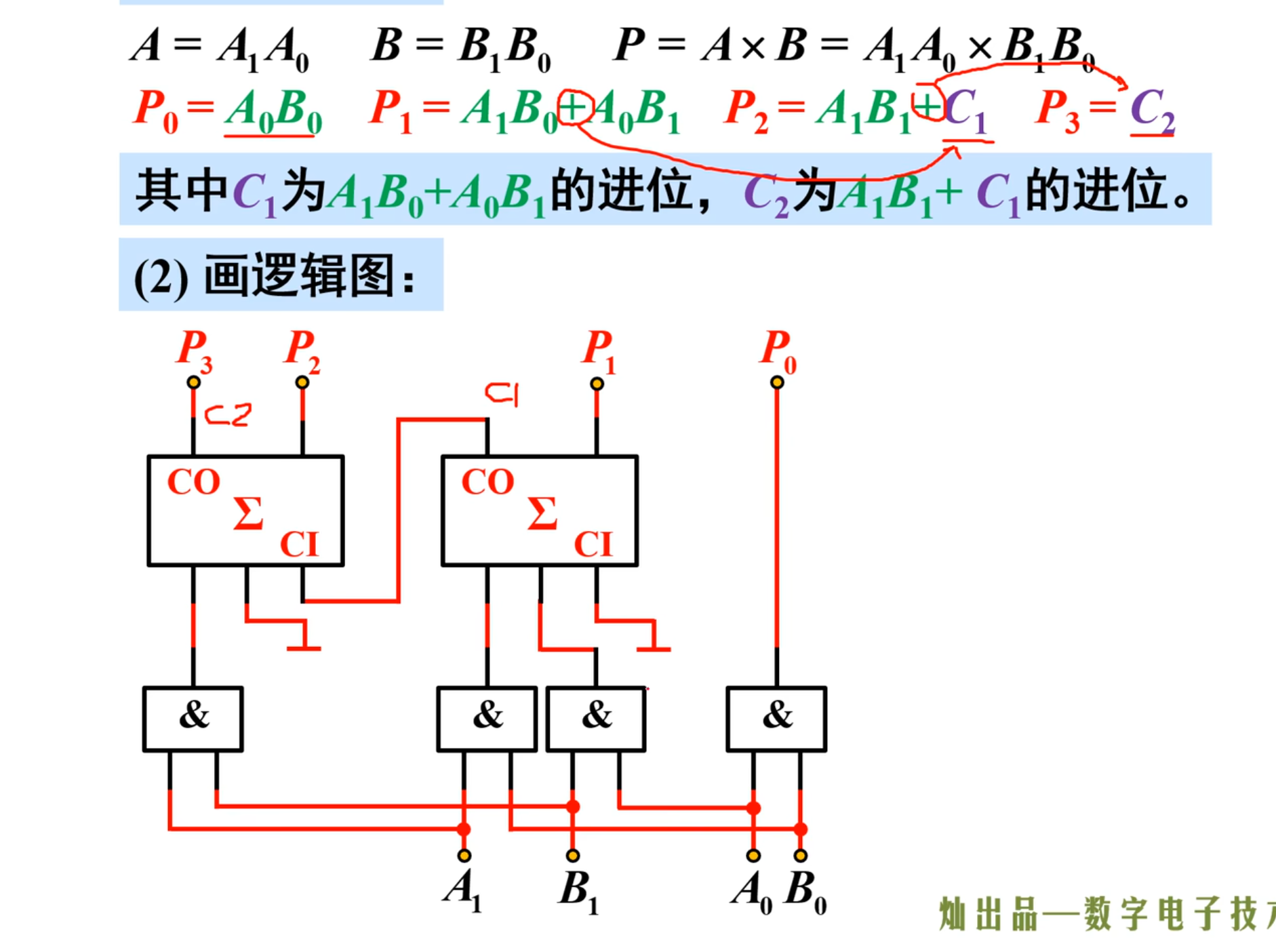
多位加法器

实现多位二进制加法运算的电路，进位方式有逐位进位（串行进位）和超前进位（并行进位）两种

NOTE

串行进位加法器：低位进位输出端依次连至相邻高位的进位输入端，最低位进位输入端接地。因此，高位数的相加必须等到低位运算完成后才能进行，运算速度较慢。

超前进位加法器：进位数直接由加法、被加数和最低位进位数形成。各位运算并行进行，运算速度快。

串行进位加法器

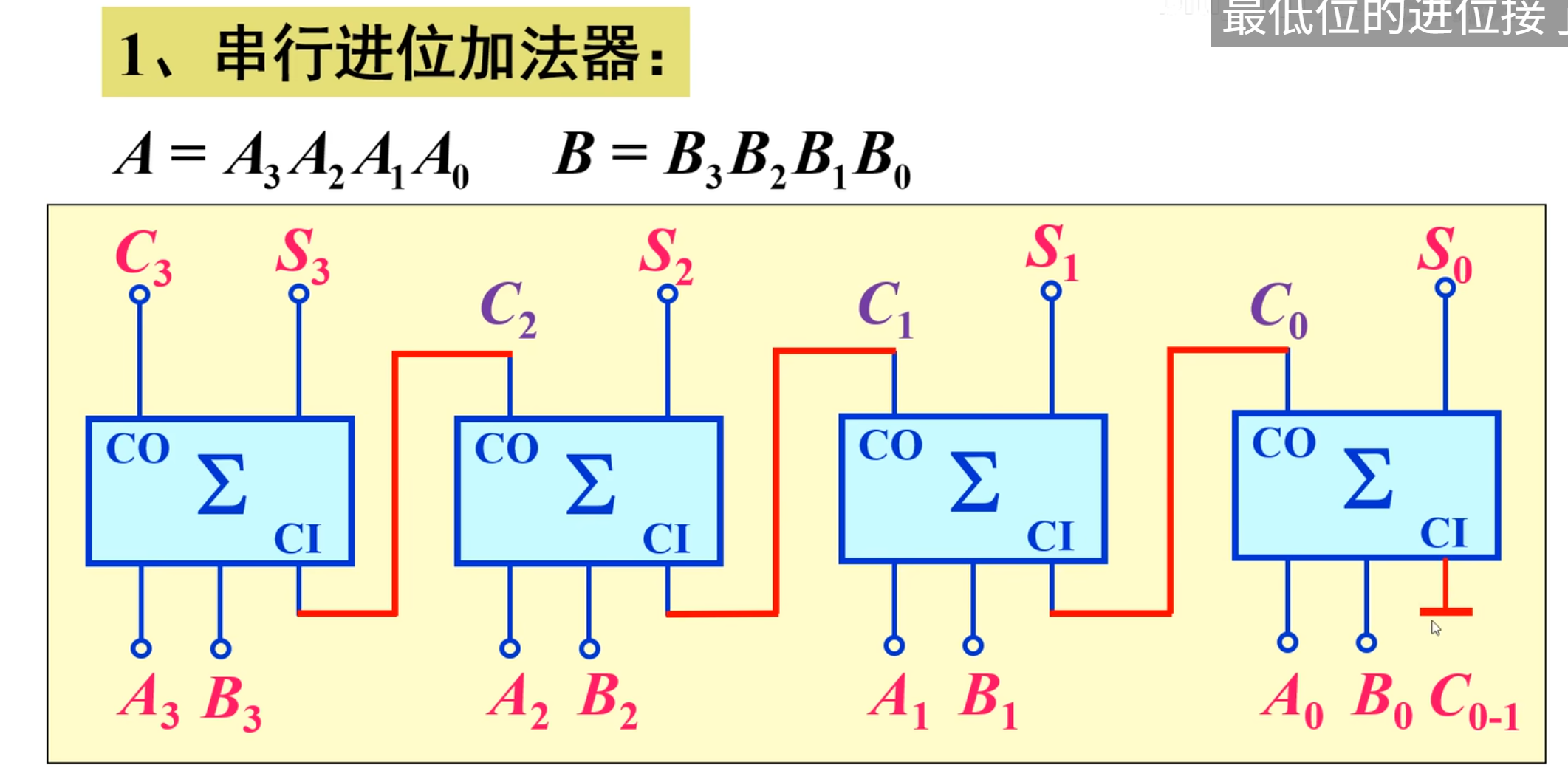
特点是 1. 电路简单，连接方便 2. 速度低

超前进位加法器 - 74 LS 283

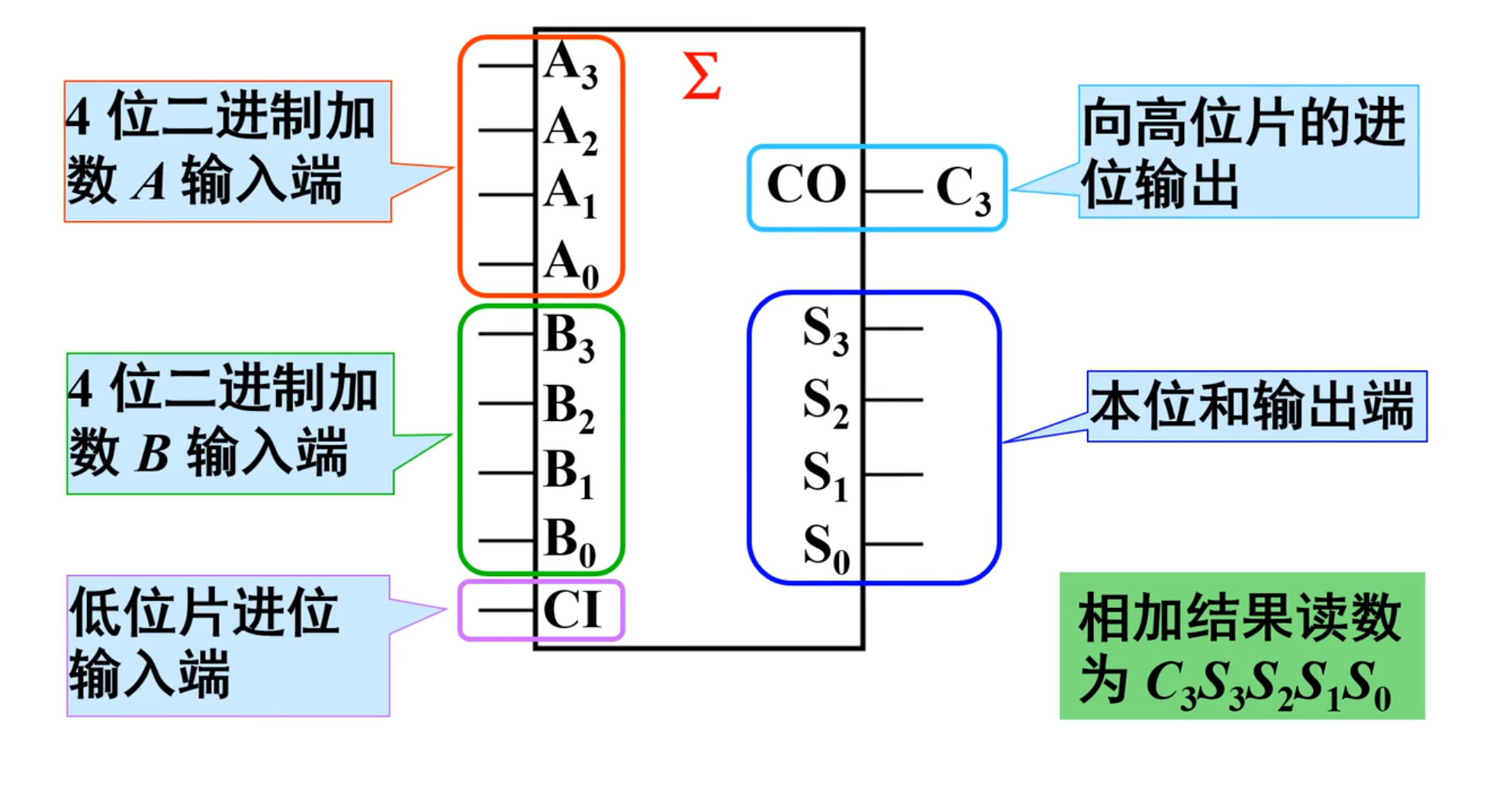
这里可以认为是利用递归的思想来实现的。

是直接将高位中需要等待低位输入的部分直接换成最低位的输入，这样就不存在等待了，因为最低位的输入部分是已知的。

不过一般是直接使用集成块来实现功能。

集成块 283 加法器的应用

应用 1 -- 8 位二进制数相加

首先是 8 位二进制数相加，原 283 加法器是 4 位二进制数相加。

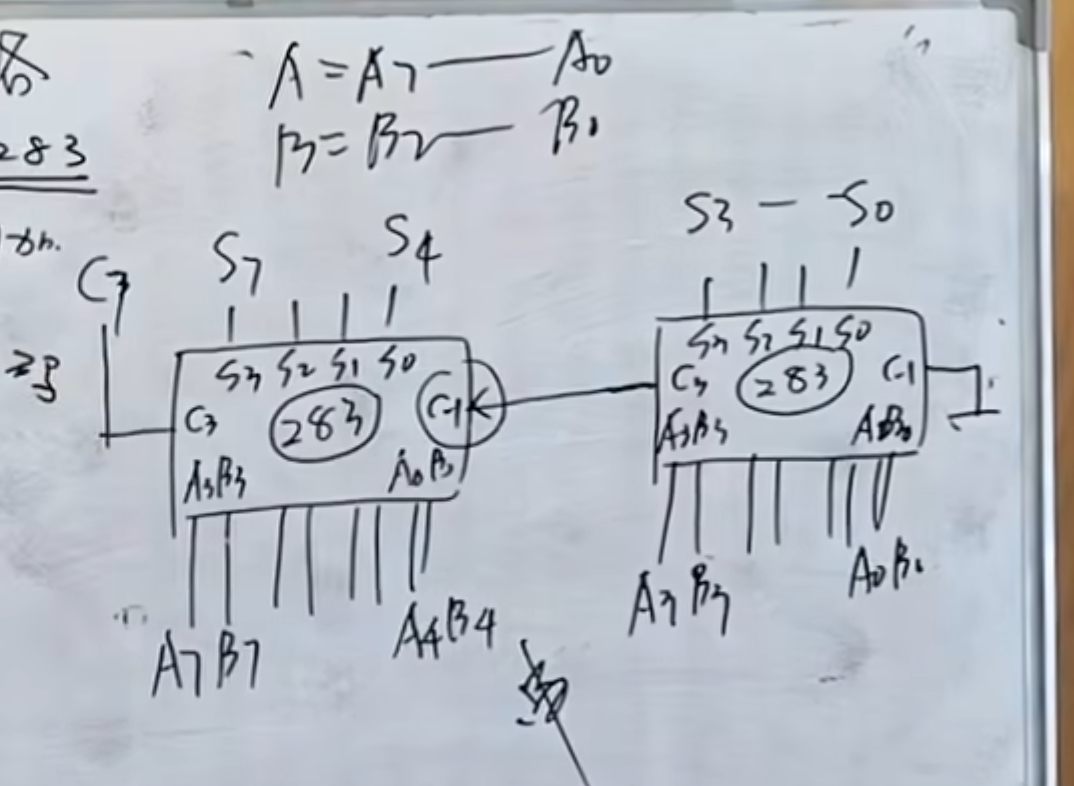
连接的方法比较简单，但是需要注意的是，两块 283 加法器之间是串联的，所以这也就导致高位需要等低位完成之后才能进行。

但 283 加法器内部是高速并行的。

应用 2 -- 8421 BCD 码转余 3 码

8421 BCD 码与余 3 码之间，只需要对 8421 BCD 码加 3 即可得到余 3 码

减法器

减法运算要用到补码。以及负数的表示。

直接用例子来说明：

设 $A=0,110$ ， $B=0,010$ ， $A$ 是 $+6$ ， $B$ 是 $+2$

注意，无论是 $A$ 还是 $B$ ，前面的哪个 $0$ 代表的是这是个正数，这一位是符号位

然后是运算 $A-B$ ， $A-B=A+(-B)$

接下来看如何求 $-B$

在进行减法运算的时候，无论是谁减谁，都需要换成补码来运算

对于正数 $A$ ，它的补码就是它本身： $A=0110$

然后是对于要求的 $-B$ ，由于 $B$ 本身是正数，取它的负数要对补码进行处理。首先是将标志位原来的 $0$ 换成 $1$ ，然后在进行取反加一

$$0010\to 1010\to 1101\to 1101+1=1110$$

然后就是进行加法运算：

$$0110+1110=1,0100$$

重点来了，在上面的加法运算中，出现了进位，那么就可以直接得到结果为 $0,100$ ；注意，这里最前面的 $0$ 依然是代表着符号位。，意思是正数.

反之，如果是 $B-A=0010-0110=-2$

首先还是 $B$ ， $B$ 是个正数，所以它的补码就是它本身，得到 $0010$ 。

然后是 $A$ ，在这里需要对 $A$ 进行处理：

$$0110\to 1110\to 1001\to 1001+1=1010$$

其中，第一步是将标志位换成 1，代表负数，然后就是再进行取反加一。

然后是计算 $0010+1010=01100$ ，最前面的代表是否有进位，如果有进位就是 $1$ ，如果没有进位就是 $0$ 。

很明显，这里是没有进位的。并且我们通过加法计算得到的其实是结果的补码： $1100$ 。

我们已知这个是负数，负数的补码再进行取反加一得到的就是原码。

注意，这里 $1100$ 前面的 $1$ 是代表负数，在进行取反加一的时候，不参与运算。

得到最后的结果是： $100\to 011\to 011+1=100$

下面是使用加法器实现减法器。

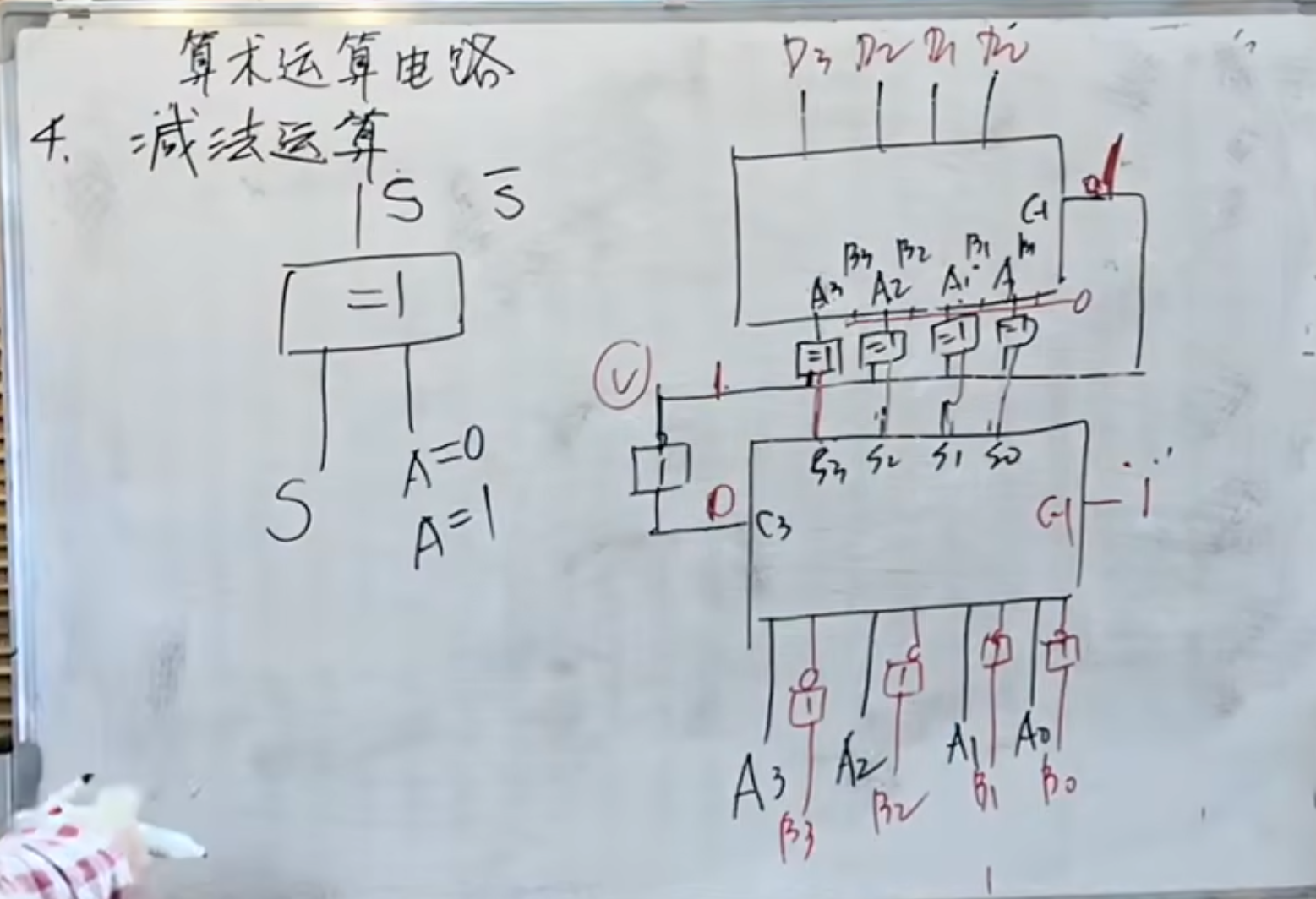
逻辑上是一样的，如果得到的结果有进位，那么就不需要再取反加一了，如果得到的结果没有进位，那么需要在进行一边取反加一。

取反使用的性质是异或门的取反性质。

数值比较器

数值比较器用于对两个数字的大小或者是否相等进行比较的逻辑电路

一位二进制数值比较器

当然，还是按照之前的分析方法来设计电路。

首先是分析设计要求，列出功能表。

设输入的两个 1 位二进制数为 $A、B$ ，输出比较的结果有三种情况： $Y_{(A>B)}$ 、 $Y_{(A=B)}$ 、 $Y_{(A<B)}$ ，有输出时为 1，否则为 0

下面直接列出真值表

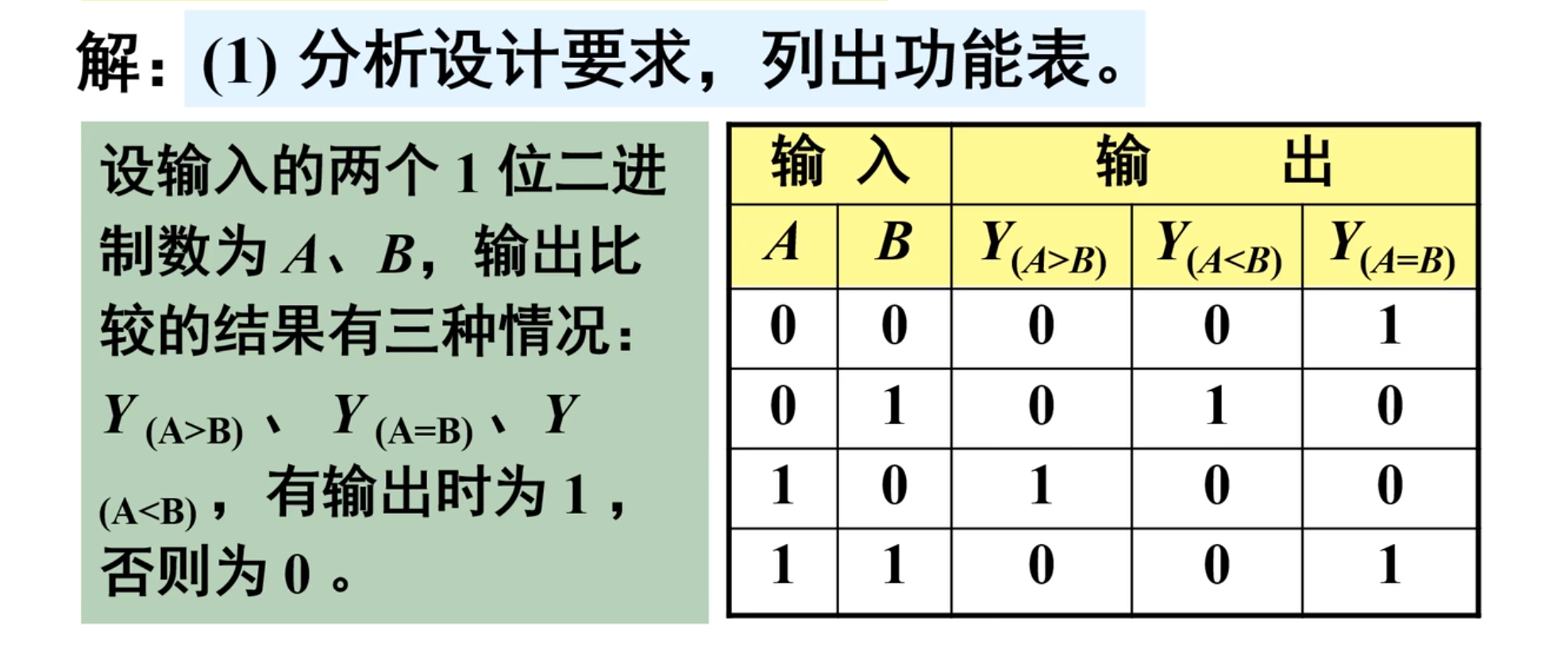
然后是根据真值表来写出逻辑函数表达式

$$\begin{array}{rl}& Y_{(A>B)}=A\bar{B}\\ & Y_{(A<B)}=\bar{A}B\\ & Y_{(A=B)}=\bar{A}\cdot \bar{B}+AB=\overline{A\oplus B}\end{array}$$

甚至于，我们可以得到这三个输出之间的关系：

$$F_{A=B}=\overline{F_{A>B}+F_{A<B}}$$

最后是画出电路逻辑图：

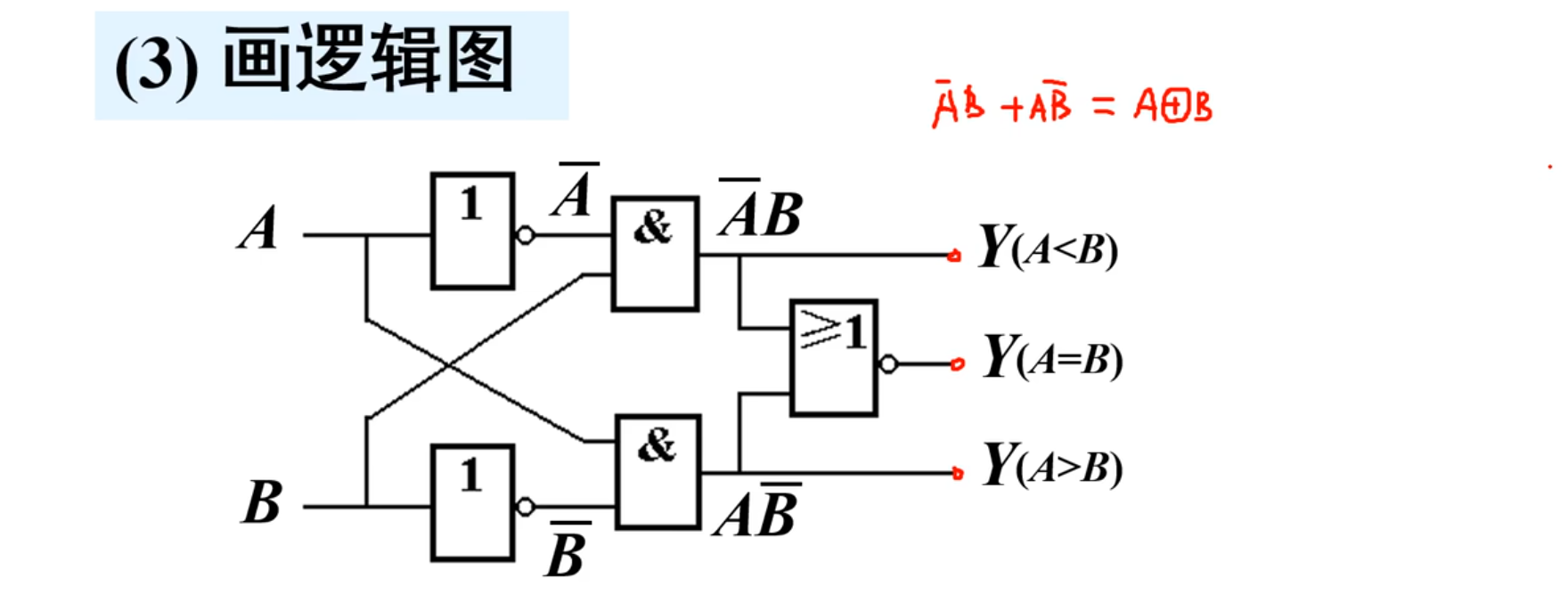
下面推广到多位数值比较器。

二位二进制数值比较器

当然，首先比较高位，然后是低位。

$$F_{A>B}=(A_1>B_1)+(A_1=B_1)\cdot (A_0>B_0)=A_1\overline{B_1}+(\overline{A_1}\cdot \overline{B_1}+A_1{B}_1)\cdot (A_0\overline{B_0})$$$$F_{A=B}=(\overline{A_1}\cdot \overline{B_1}+A_1{B}_1)\cdot (\overline{A_0}\cdot \overline{A_0}+A_0{B}_0)$$$$F_{A<B}=(\overline{A_1}{B}_1)+(\overline{A_1}\cdot \overline{B_1}+A_1{B}_1)\cdot (\overline{A_0}{B}_0)$$

如何使用两个一位二进制数值比较器来实现二位二进制数值的比较呢？

具体接线如下图所示。

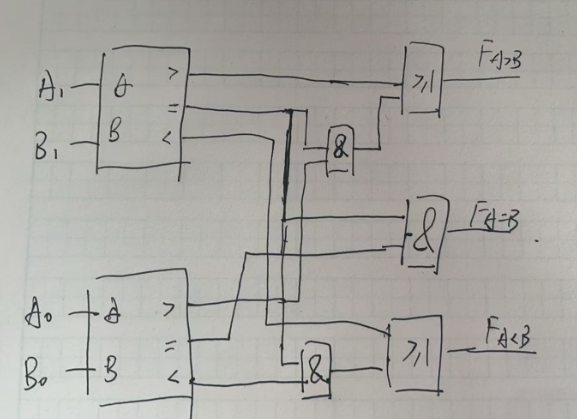
多位数值比较器

NOTE

比较原理：从最高位开始逐位向低位进行比较

举个例子：

比较 $A=A_3{A}_2{A}_1{A}_0$ 和 $B=B_3{B}_2{B}_1{B}_0$ 的大小：

若 $A_3>B_3$ ，则 $A>B$ ；若 $A_3<B_3$ ，则 $A<B$ ；若 $A_3=B_3$ ，则需要比较次高位

若次高位 $A_2>B_2$ ，则 $A>B$ ；若 $A_2<B_2$ ，则 $A<B$ ；若 $A_2=B_2$ ，则再去比较更低位。

以此类推，直到最低位比较结束

这里就需要使用集成块来实现了

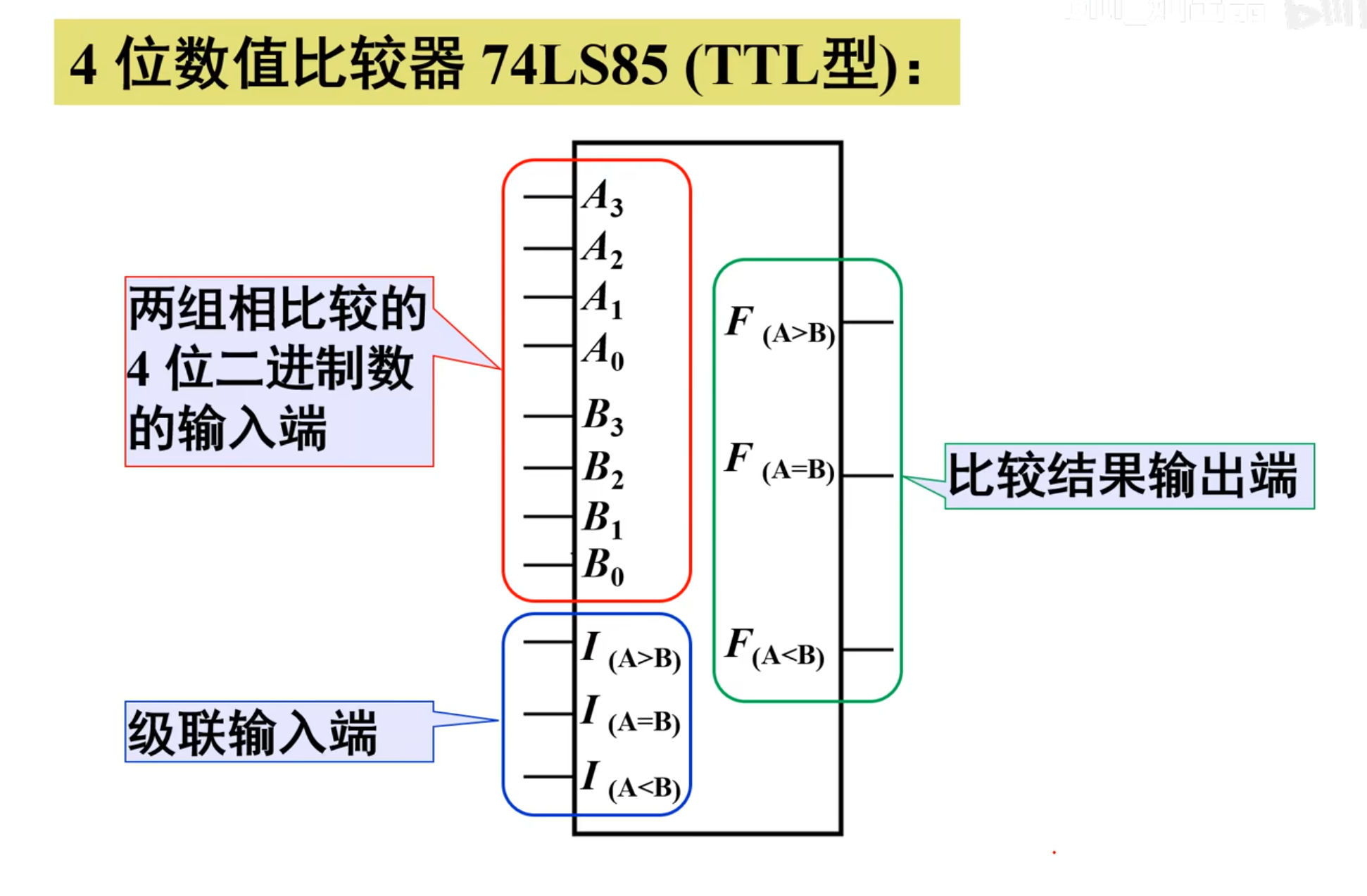
在上面这个比较器中，有三个级联输入端，意味着如果这个两个四位二进制数，都相等，那么最后的结果则是根据这个级联输入端来判断的。具体看下面这个功能表。

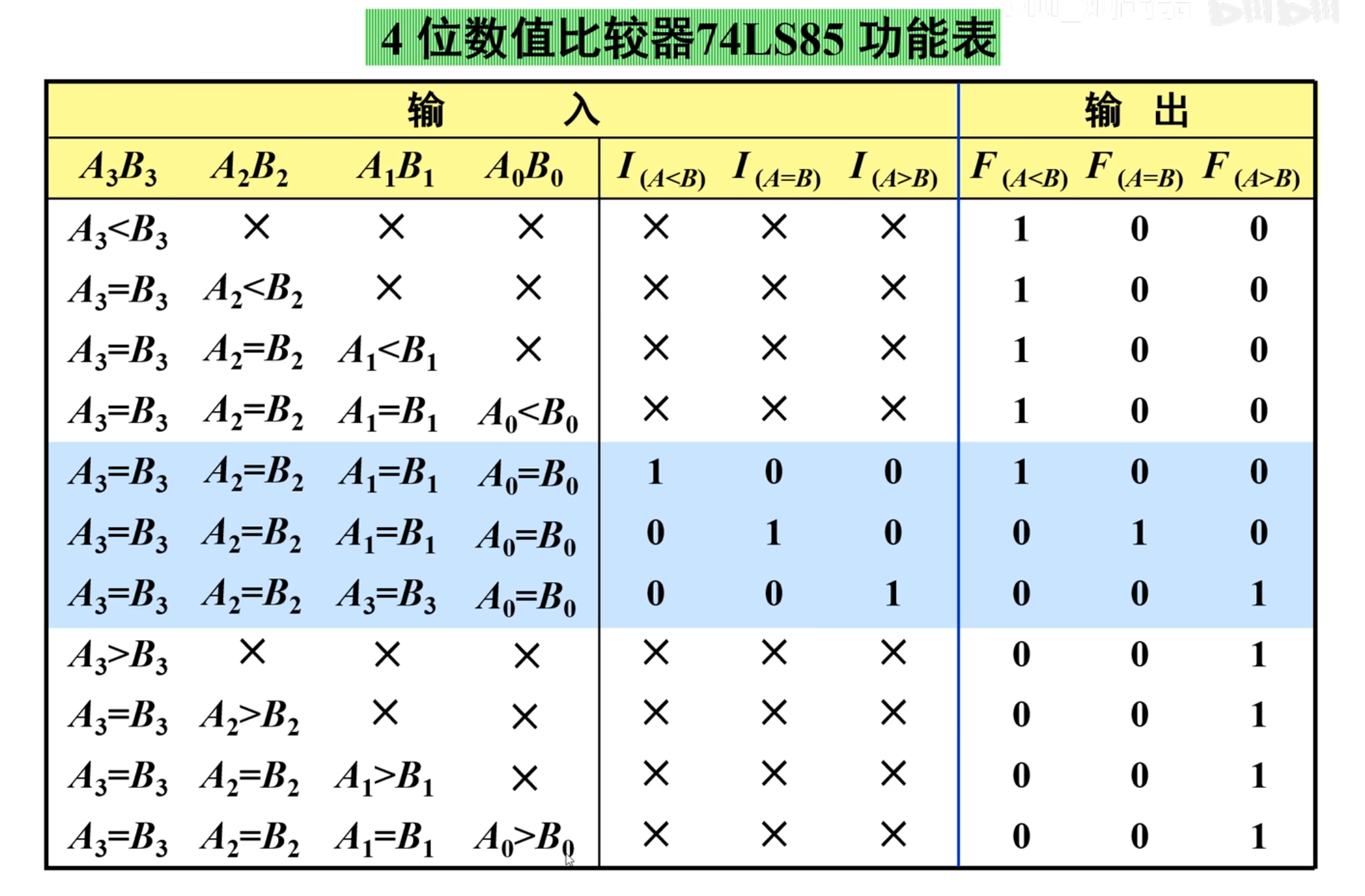
下面是 74 LS 85 的使用说明：

1. 当只比较两个 4 位二进制数时，或不使用扩展端（意味着此比较器作为低位使用）时，将扩展端的 $I_{(A=B)}$ 接 1， $I_{(A<B)}$ 和 $I_{(A>B)}$ 接 $0$ 。其实 $I_{(A<B)}$ 和 $I_{(A>B)}$ 在这时取什么都是可以的，但是为了方便来说，取 $0$ ；这样的话，对于低位来说，相当于再低位的比较结果是相等的，那么就再去比较高位即可。

2. 当比较两个 4 位以上 8 位以下的二进制数时，应先比较两个高 4 位的二进制数，在高位相等时，才能比较低 4 位数。只有在两个 4 位二进制数相等时，输出才由扩展端 $I_{(A>B)}、I_{(A<B)}、I_{(A=B)}$ （相当于再去由低位决定）决定。

下面是用两个 74 LS 85 来级联成 8 位数值比较器

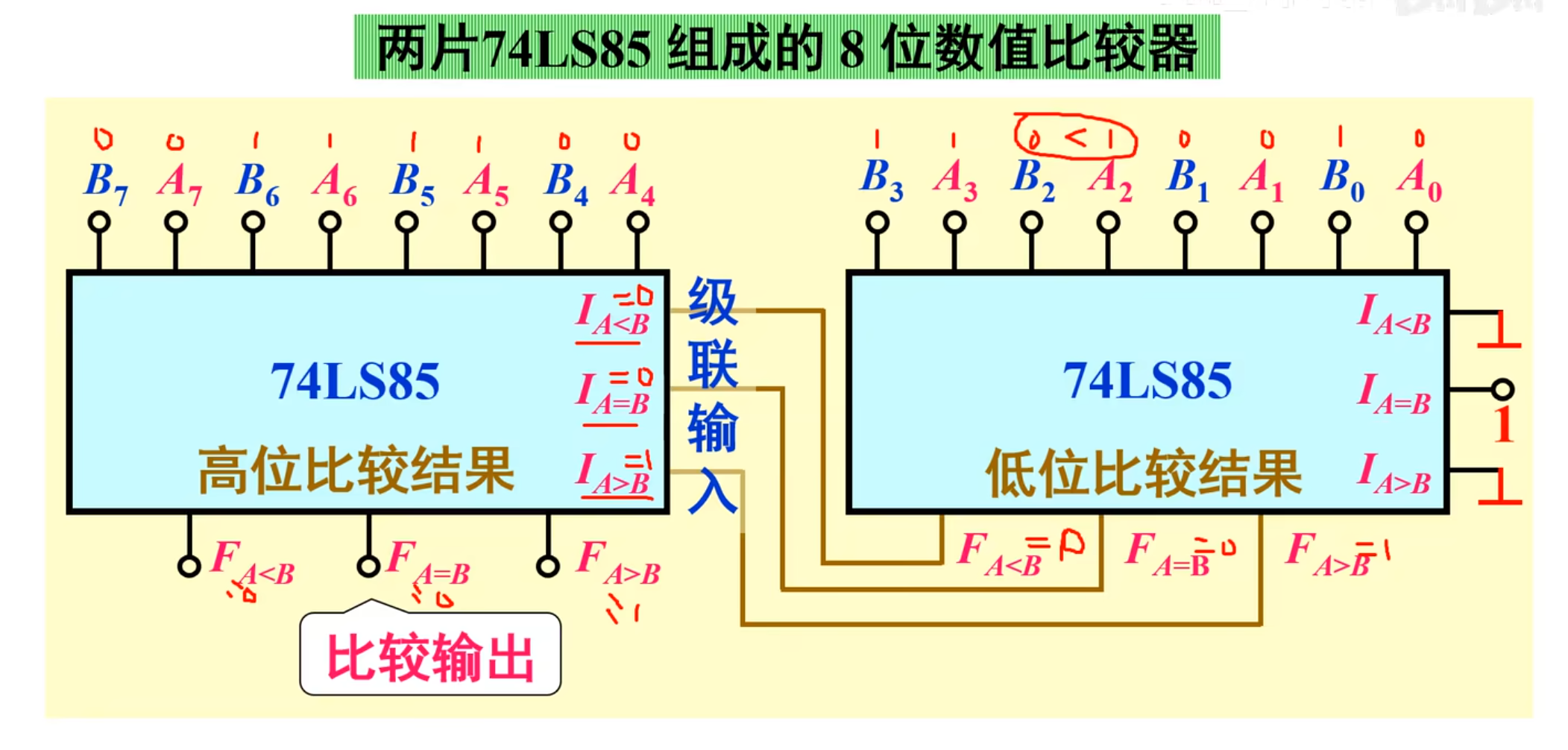
如果是十六位的，那么可以将四个 4 位二进制数值比较器串联起来，也是可以实现十六位的二进制数值比较。

下面是使用并联的形式，来实现十六位的二进制数值的比较

并联，就需要使用 5 个二进制数值比较器。

连接方法如下：

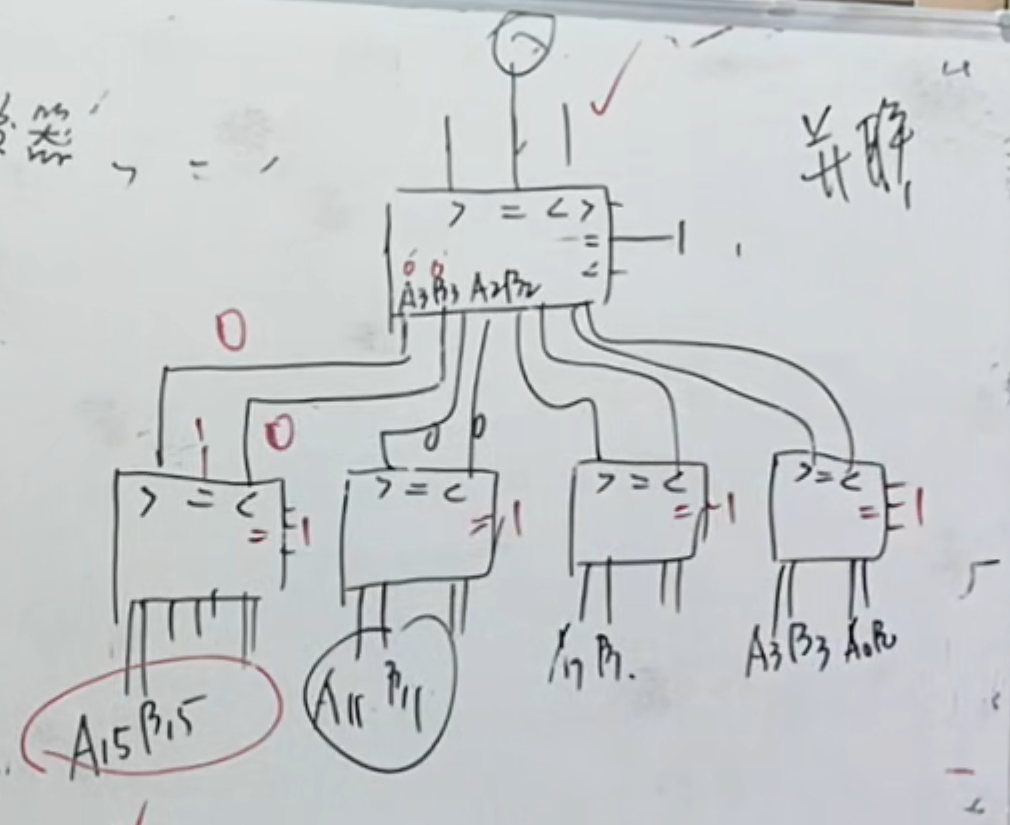
NOTE

关键在于第二级连接，由于第一级输出的是逻辑结果，那么只需要比较是否存在大于小于的情况，至于等于的情况，不需要考虑在内，原因在于如果在第一级上出现等于，那么相应的，大于小于的输出一定是 $0$ ，再输入到二级中的时候，输入就已经相当于是相等的了

编码器和译码器

编码器

NOTE

编码：用文字、符号或数字来表示特定对象的过程。

在数字电路中，采用二进制进行编码

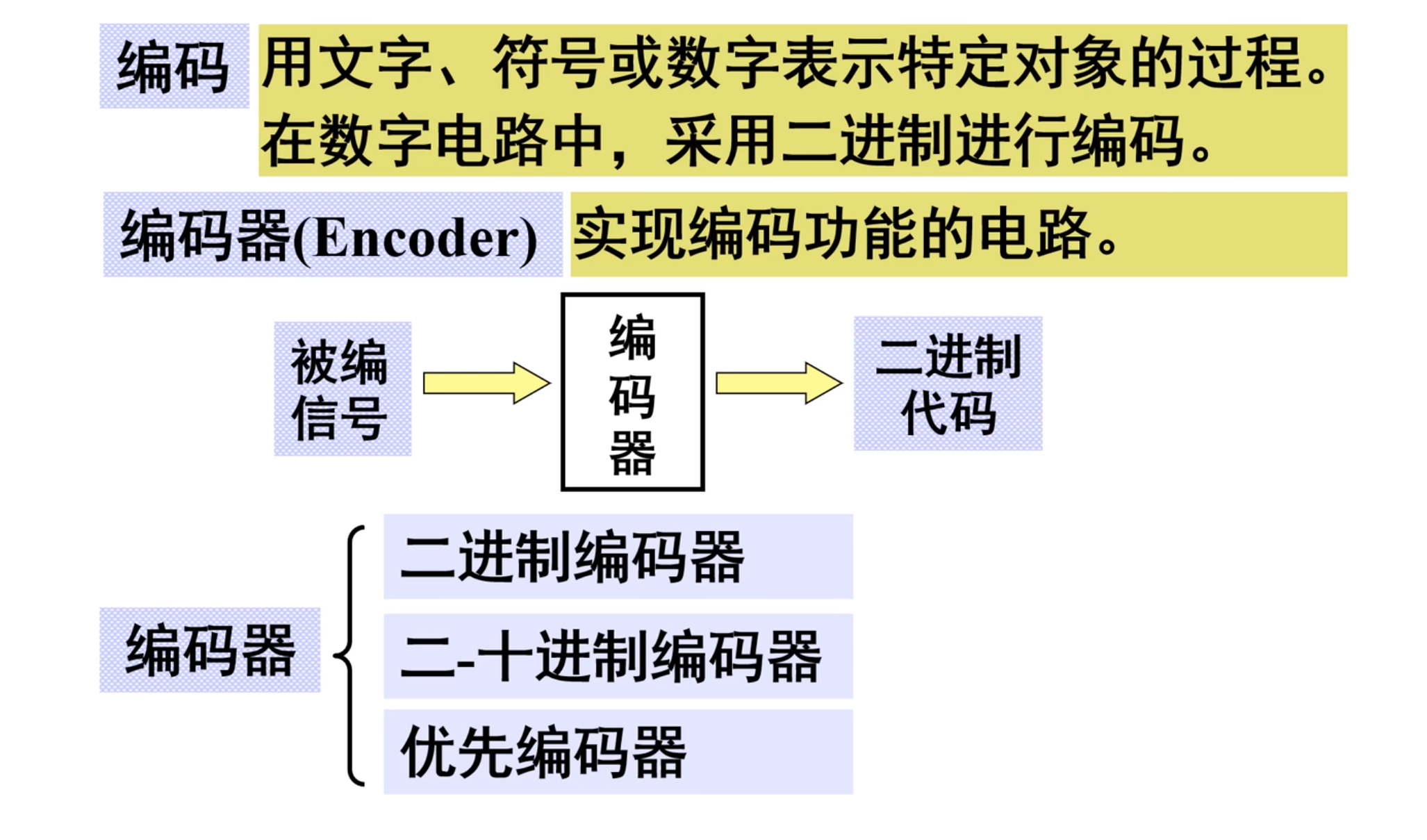
下面来看一下输入信号与输出位数之间的关系

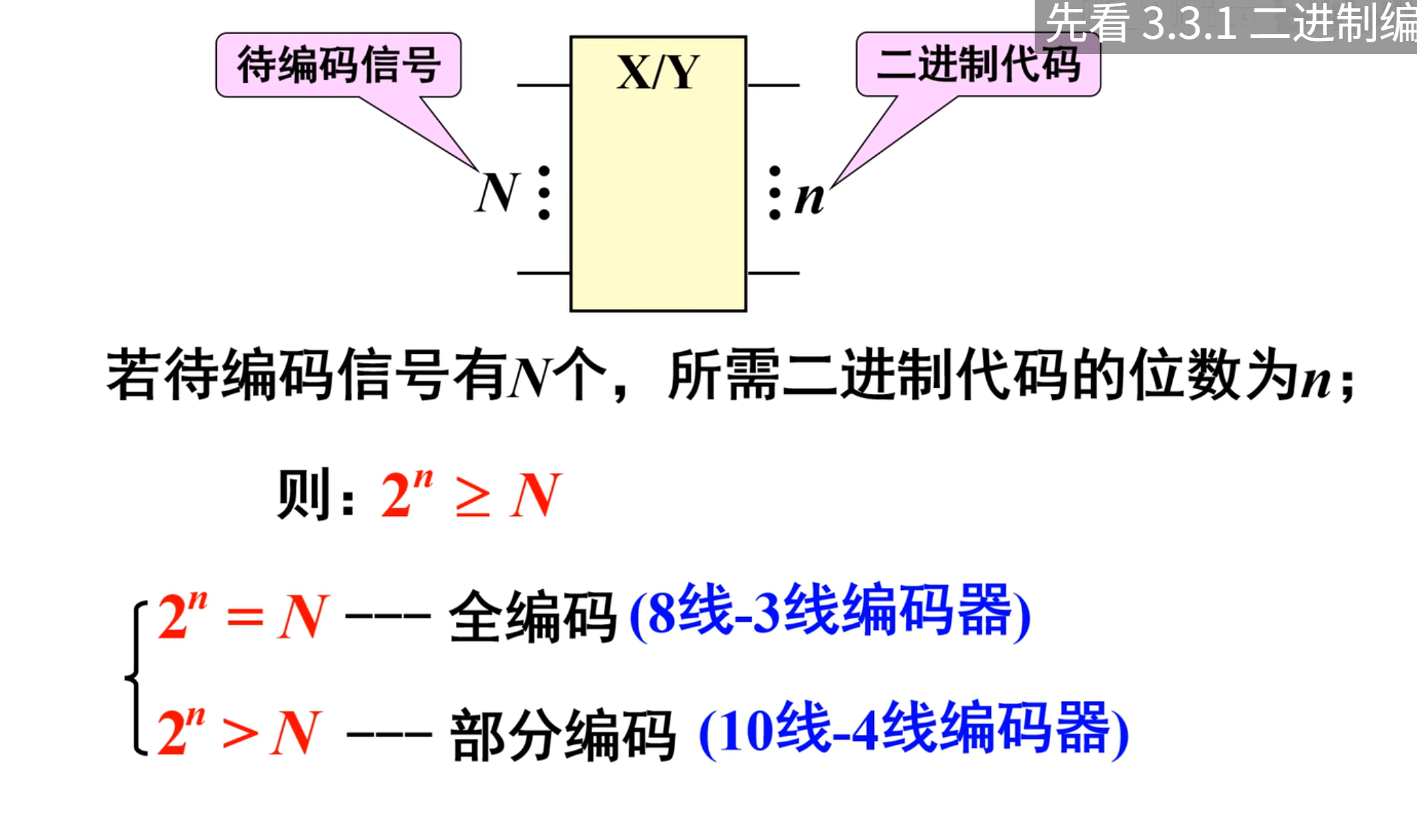
这个说明的是如果有 8 个待编码的信号，那么至少需要 3 位二进制代码数。

如果只有 6 个待编码的信号，那么也需要 3 位二进制代码数。

二进制编码器

二进制编码器是将 $N=2^n$ 个输入信号转换成 $n$ 位二进制代码的逻辑电路。

比如说下面这个例题：

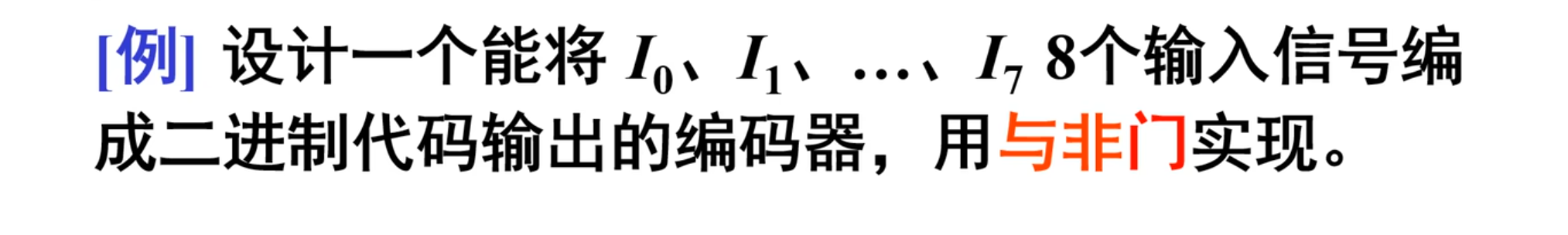
当然，这个例题依然是按照之前求解实际问题的方法（组合逻辑电路的设计）来解决。

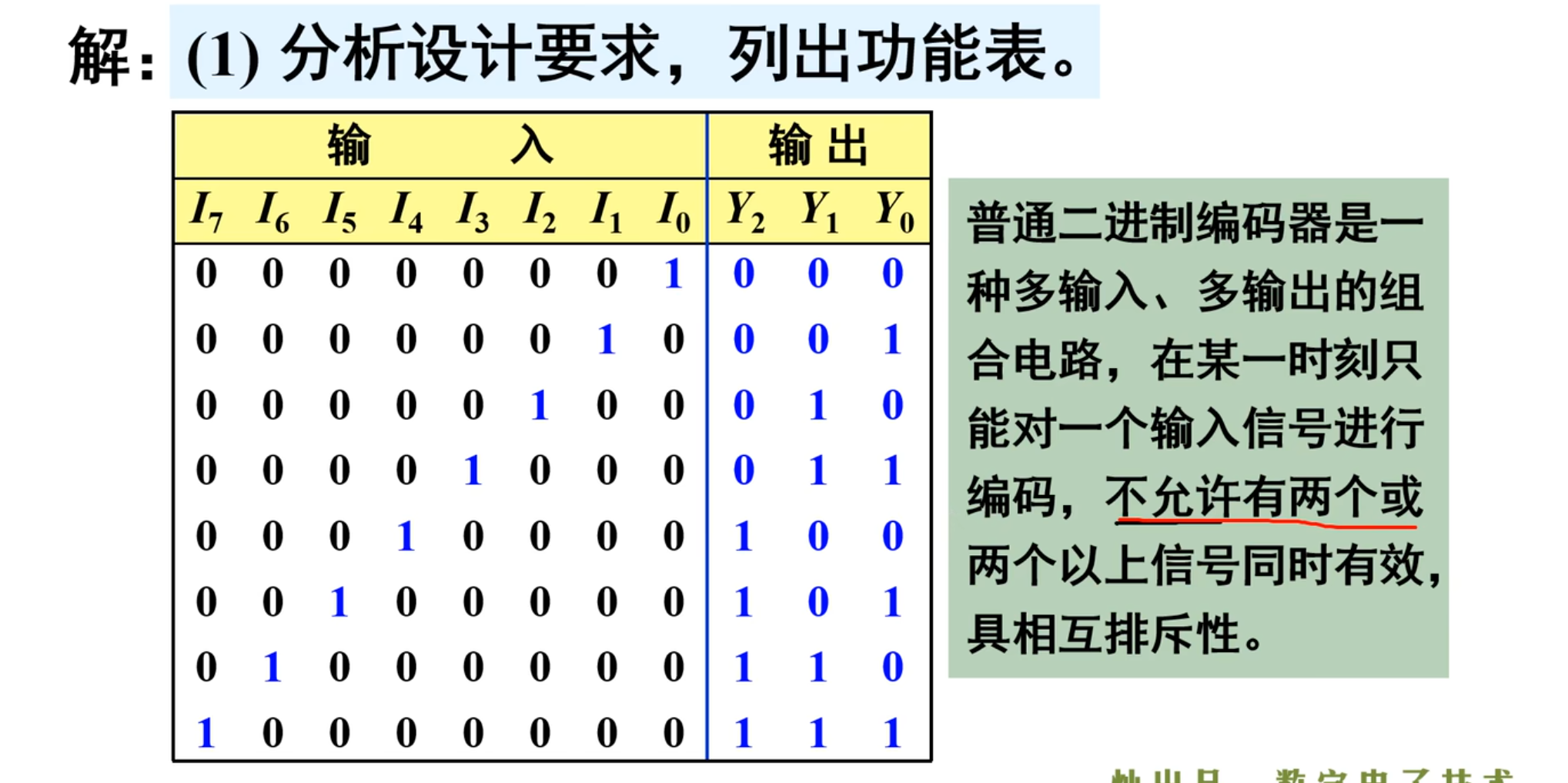
首先是分析设计要求，列出功能表。

由题意可知，该编码器有 8 个输入信号，分别是 $I_0$ 、 $I_1...$ $I_7$ ，有编码请求时，输入信号用 1 表示，没有时为 0。根据 $2^n\ge N=8$ 可求得输出 $n=3$ ,为 3 位二进制代码，分别用 $Y_0$ 、 $Y_1$ 、 $Y_2$ 表示。

NOTE

普通的二进制编码器是一种多输入、多输出的组合电路，在某一时刻只能对一个输入信号进行编码，不允许有两个或两个以上的信号同时有效，具有相互排斥性。

如下面的真值表。

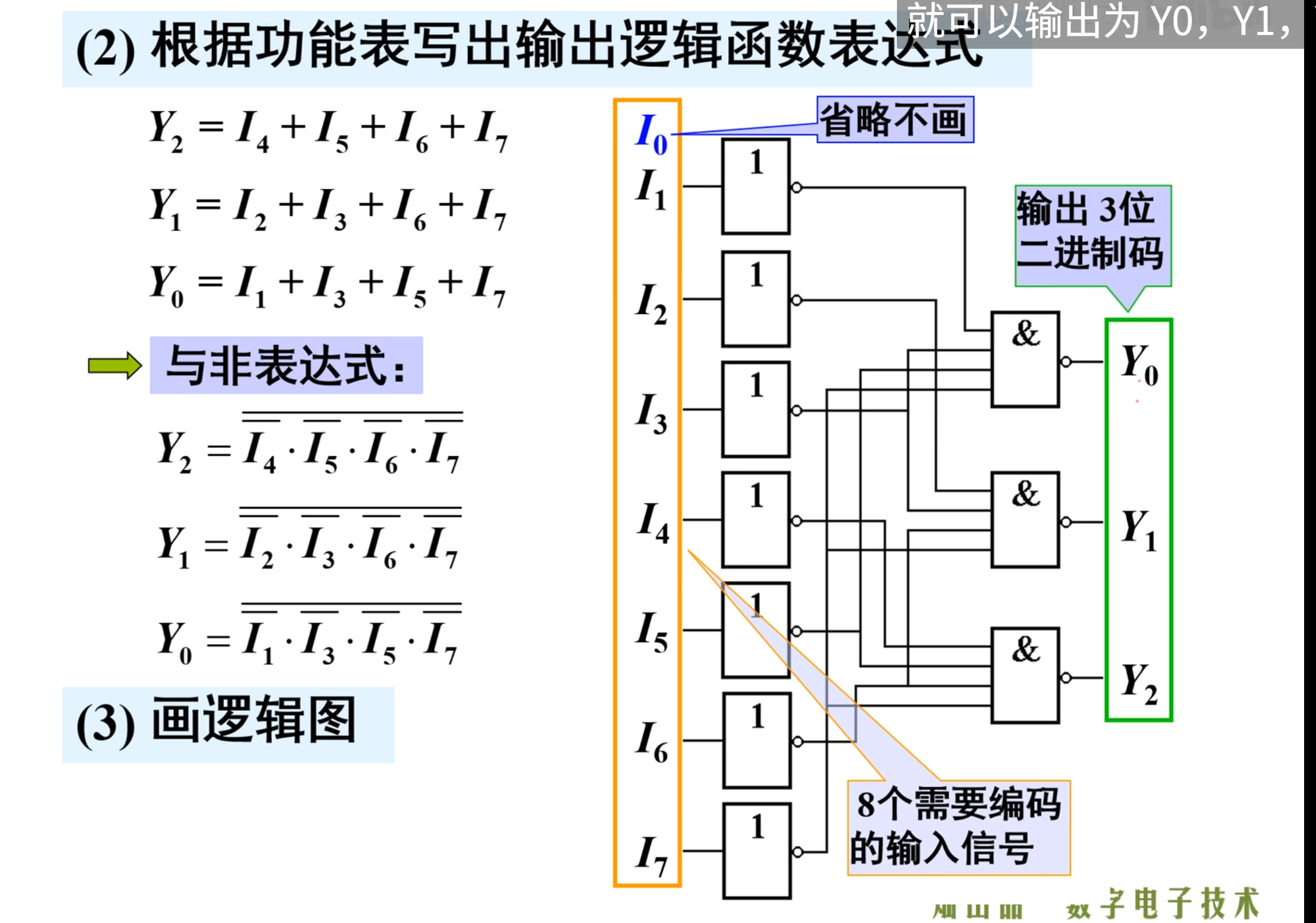
然后是根据真值表写出输出逻辑函数表达式；

$$\begin{array}{rl}{Y}_2& =I_4+I_5+I_6+I_7\\ Y_1& =I_2+I_3+I_6+I_7\\ Y_0& =I_1+I_3+I_5+I_7\end{array}$$

这里直接就看其输出为 1 的对应的输入上的信号即可。本质上是吸收律

然后换到与非式：

$$\begin{array}{rl}{Y}_2& =\overline{\stackrel{―}{I_4}\cdot \stackrel{―}{I_5}\cdot \stackrel{―}{I_6}\cdot \stackrel{―}{I_7}}\\ Y_1& =\overline{\stackrel{―}{I_2}\cdot \stackrel{―}{I_3}\cdot \stackrel{―}{I_6}\cdot \stackrel{―}{I_7}}\\ Y_0& =\overline{\stackrel{―}{I_1}\cdot \stackrel{―}{I_3}\cdot \stackrel{―}{I_5}\cdot \stackrel{―}{I_7}}\end{array}$$

下面画出逻辑图

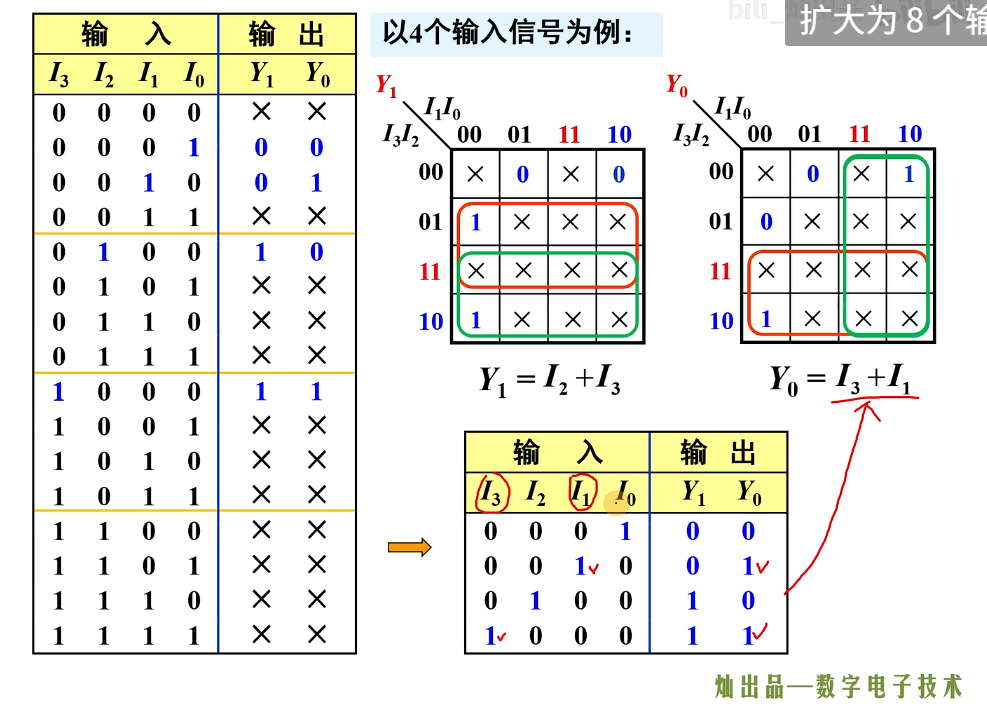
下面这个是以 4 个信号为例子，用卡诺图化简的方法实现为什么 $Y_1=I_2+I_3$

进而得到的结果是下面这个，后续可以直接使用这种方法从而快速的求解输出对应输入之间的关系。

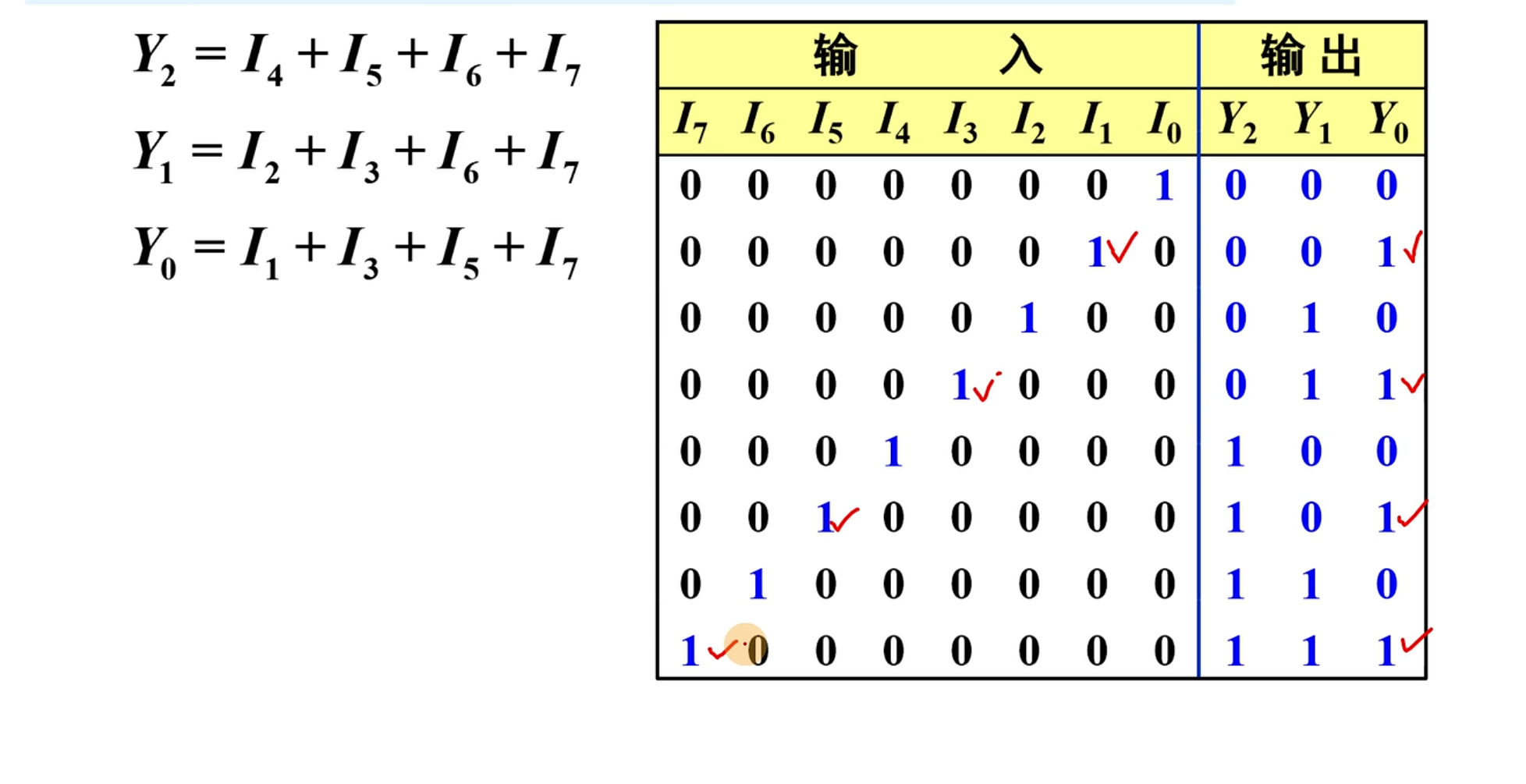
二-十进制编码器

用二进制数对十进制数进行编码

依然是通过例题来解答：

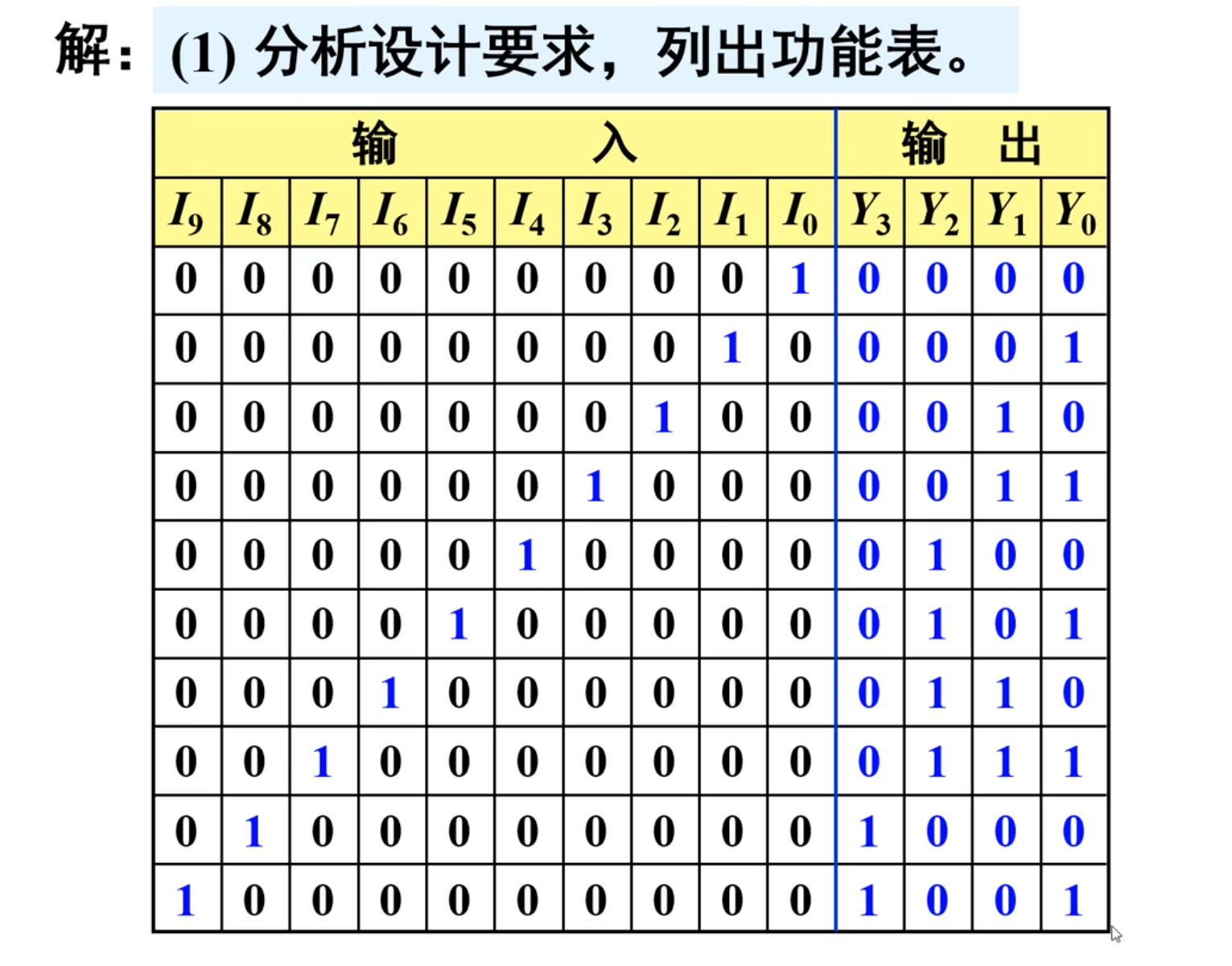
下面来分析设计要求，列出功能表。

由题意可知，该编码器有 $I_0$ 、 $I_1...I_9$ 10 个输入信号，有编码请求时，输入信号为 1，没有时为 0。根据 $2^n\ge N=10$ 可求得输出 $n=4$ ，故有 4 个输出端，分别用 $Y_0$ 、 $Y_1$ 、 $Y_2$ 、 $Y_3$ 表示。

这种编码是不完全编码

IMPORTANT

注意，在这种编码中，不一定是用什么方法来进行编码，这个题目是编码成 8421 BCD 码，当然可以能是其他的顺序。

然后是根据真值表来写出逻辑函数表达式

$$\begin{array}{rl}{Y}_3& =I_8+I_9\\ Y_2& =I_4+I_5+I_6+I_7\\ Y_1& =I_2+I_3+I_6+I_7\\ Y_0& =I_1+I_3+I_5+I_7+I_9\end{array}$$

然后换成与非表达式得到：

$$\begin{array}{rl}& Y_3=\overline{\stackrel{―}{I_8}\cdot \stackrel{―}{I_9}}\\ & Y_2=\overline{\stackrel{―}{I_4}\cdot \stackrel{―}{I_5}\cdot \stackrel{―}{I_6}\cdot \stackrel{―}{I_7}}\\ & Y_1=\overline{\stackrel{―}{I_2}\cdot \stackrel{―}{I_3}\cdot \stackrel{―}{I_6}\cdot \stackrel{―}{I_7}}\\ & Y_0=\overline{\stackrel{―}{I_1}\cdot \stackrel{―}{I_3}\cdot \stackrel{―}{I_5}\cdot \stackrel{―}{I_7}\cdot \stackrel{―}{I_9}}\end{array}$$

下面是画出电路逻辑图

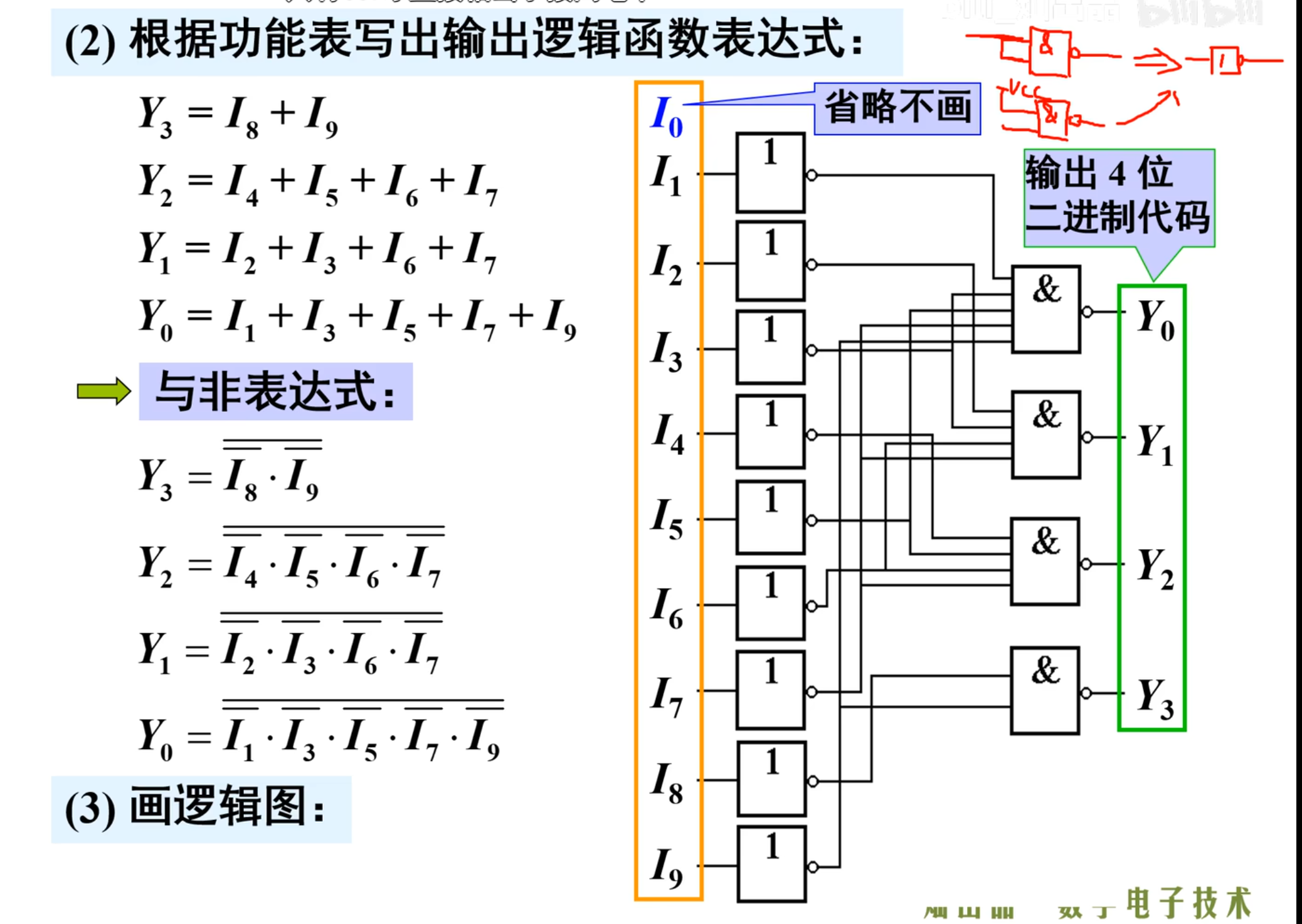
按照题目的要求是要用与非门来实现，但是上面图中用的不全是与非门，当然也可以用直接用与非门来表示非门，具体方法在上面图中的右上角。

十进制编码器补充

针对十进制编码器，其主要实现的逻辑电路如下图所示。

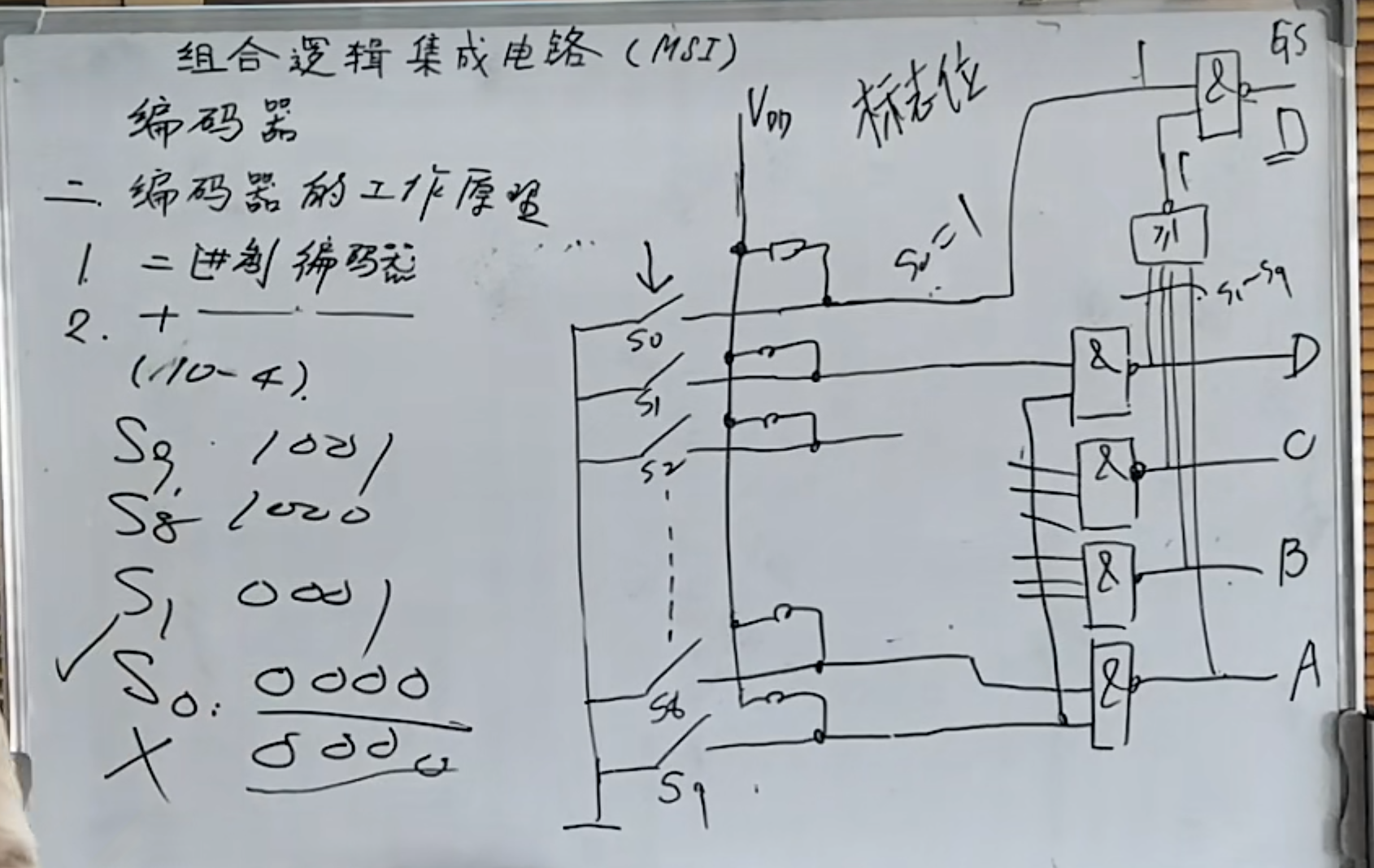
这里的问题在于对于输入 $0$ 的编码，设置成了 $0000$ ，但是在电路中，如果什么也不按，其输出的编码结果与 $0000$ 的编码结果是一样的。这样会无法区分是什么也没按，还是只按了 $0$

所以添加一个标志位，当标志位为 $0$ 的时候，表示什么也没按。

其逻辑设计也在上面图中表示。

其功能表图下图所示：

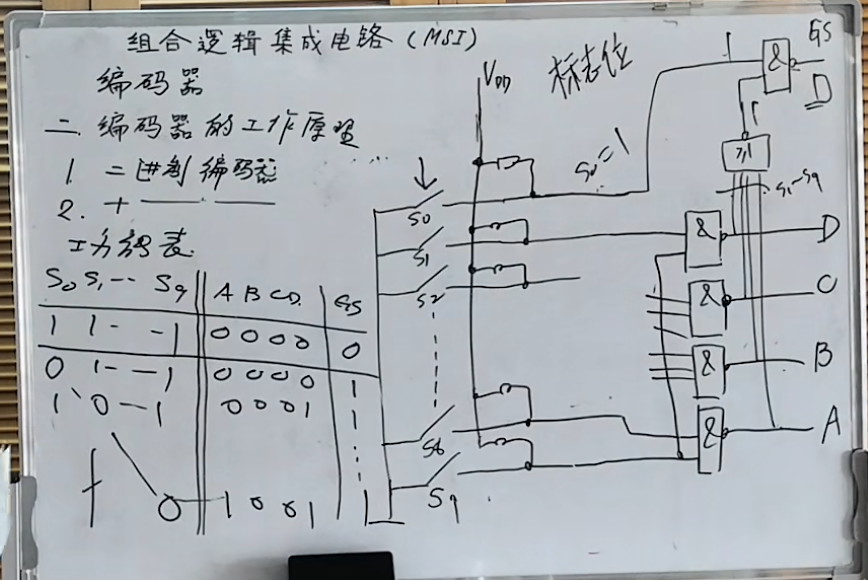
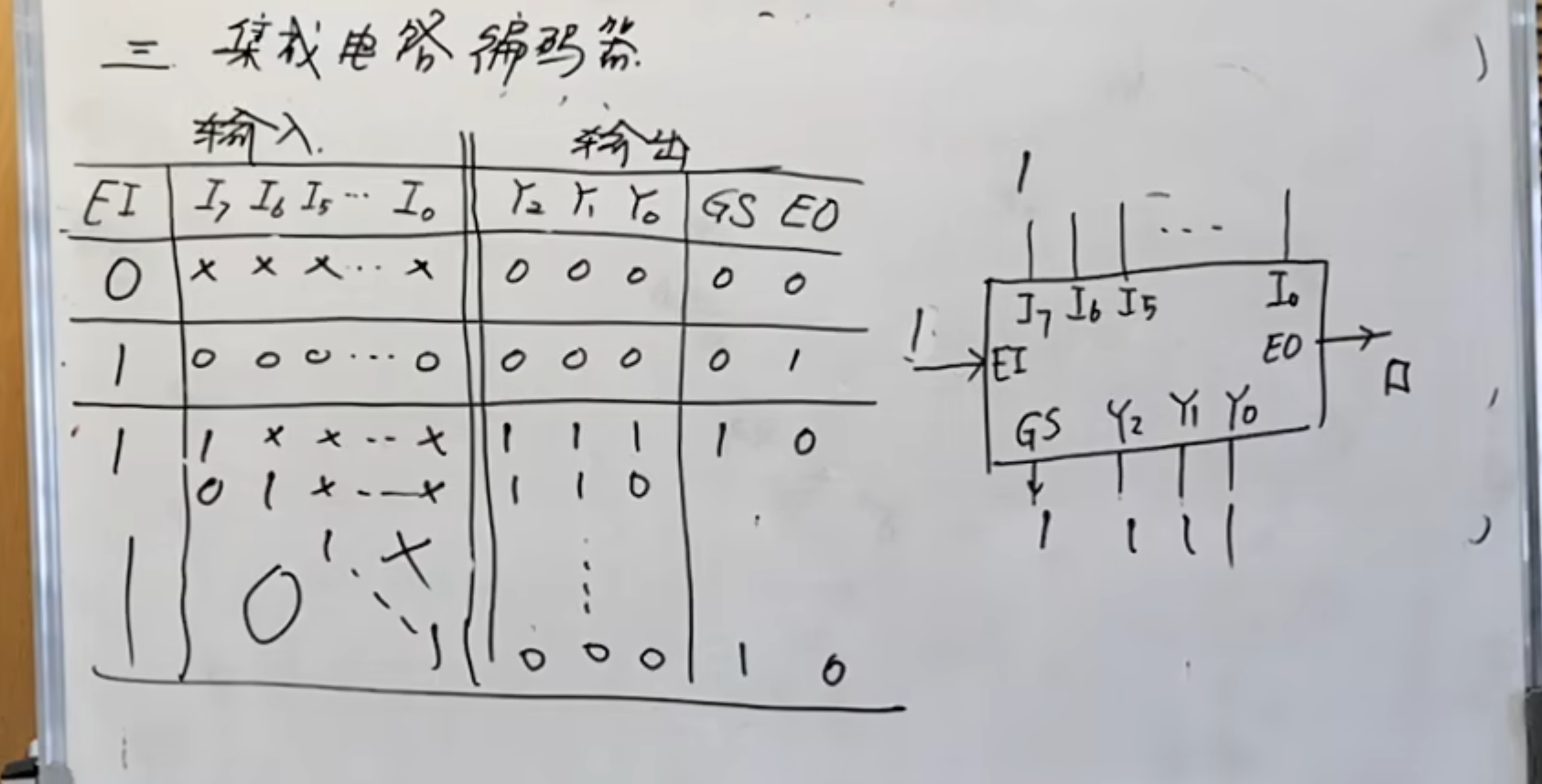
优先编码器

基本优先编码器

之前讲的编码器都是只能单个信号有效，但是在很多场合不只是单个信号，而多个信号就涉及到优先级的问题

优先编码器允许同时输入多个编码信号，并且只对其中优先级别高的信号进行编码输出的信号。

NOTE

下面假设 $I_7$ 的优先级最高， $I_6$ 次之，依次到 $I_0$ 最低。优先级高的信号排优先级低的，具有单方面排斥的特性。

而在优先级之后的部分无论是有效还是无效都无所谓了。用 $X$ 来表示。

真值表如下图所示。

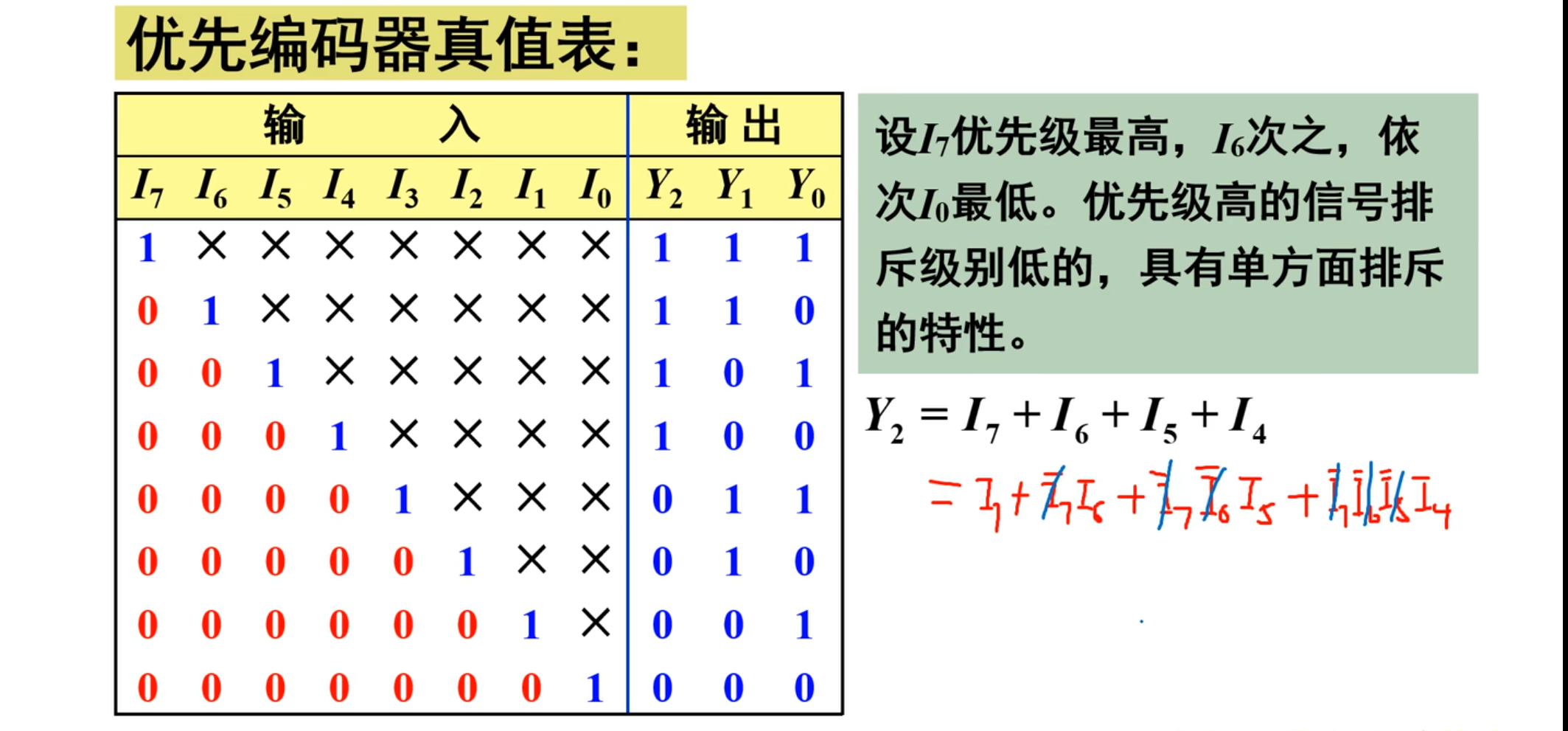
需要注意的是，在输出表达的时候，是根据优先级来计算出来的，依然是看对应的部分是如何取值的。而推导则是上面图中的红色部分，用到的是吸收率

$$\begin{array}{c}{Y}_2=I_7+I_6+I_5+I_4\\ Y_1=I_7+I_6+\overline{I_5}\overline{I_4}{I}_3+\overline{I_5}\overline{I_4}{I}_2\\ Y_0=I_7+\overline{I_6}{I}_5+\overline{I_6}\overline{I_4}{I}_3+\overline{I_6}\overline{I_4}\overline{I_2}{I}_1\end{array}$$

NOTE

注意，上面这里不是全部的非都被消去了。有一部分没办法被消去。

下面用四个输入信号作为例子以卡诺图化简的方法来进行说明，

首先需要注意的是，在输出部分，由于 $I_3$ 输入为 1，后面的输入无论是什么都不影响输出，将这个时候的输出都设置为 1，所以 $Y_1=Y_0=1$ 。

然后是当 $I_3=0$ 、 $I_2=1$ 的时候，后面的输入无论是什么都不影响输出，设置这个时候的输出为 $Y_1=0$ ， $Y_0=0$

以此类推，当 $I_3=0$ ， $I_2=0$ ， $I_1=1$ 的时候，后面的输入无论是什么都不影响输出，设置这个时候的输出为 $Y_1=0$ ， $Y_0=1$

当 $I_3=0$ ， $I_2=0$ ， $I_1=0$ 、 $I_0=1$ 的时候，后面的输入无论是什么都不影响输出，设置这个时候的输出为 $Y_1=0$ ， $Y_0=0$

而当输入都为 0 的时候，输出的结果就是无关项了。

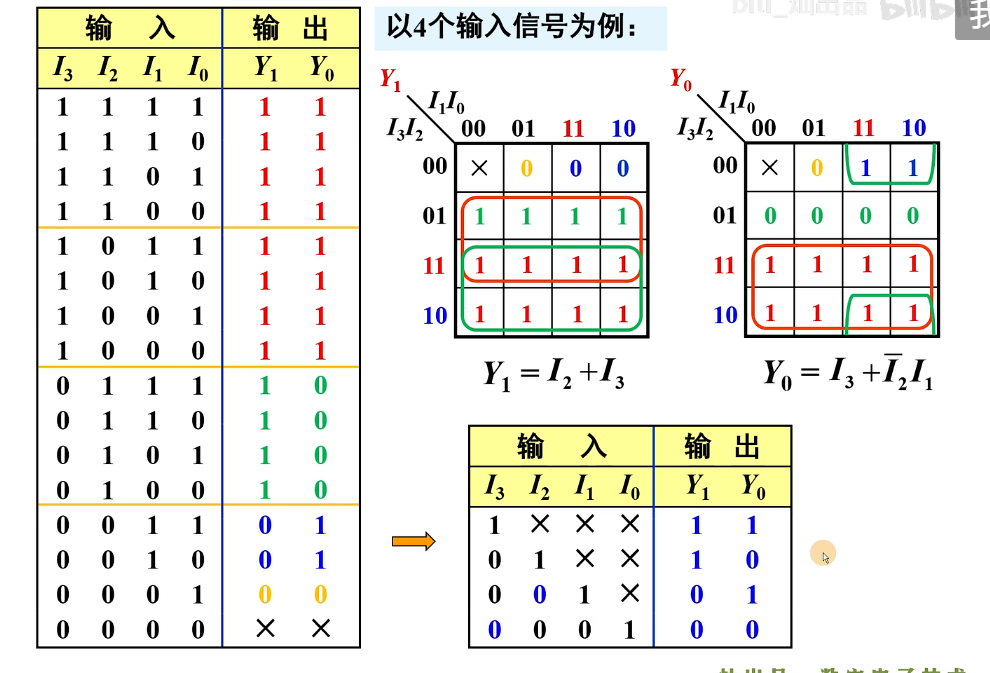
然后将上面的真值表化简一下，得到右侧的真值表。

最后在这个真值表上找规律：

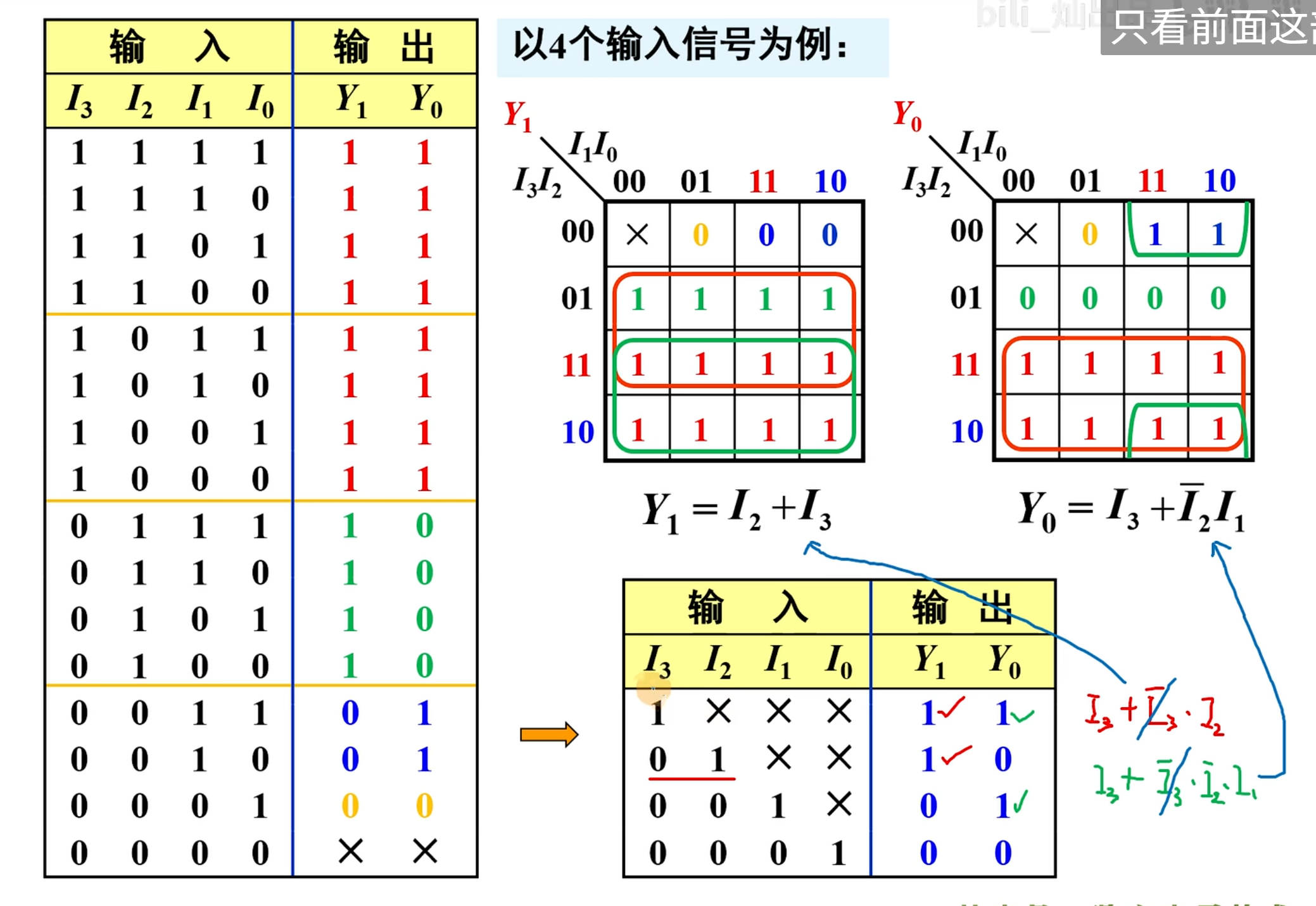
NOTE

在进行计算的时候，只看交叉 (X) 前面的部分，例如 $Y_1=I_3+\overline{I_3}\cdot I_2=I_3+I_2$ ， $Y_2=I_3+\overline{I_3}\cdot \overline{I_2}\cdot I_1=I_3+\overline{I_2}\cdot I_1$

通过上面这个方法，再将其推广到八个变量。

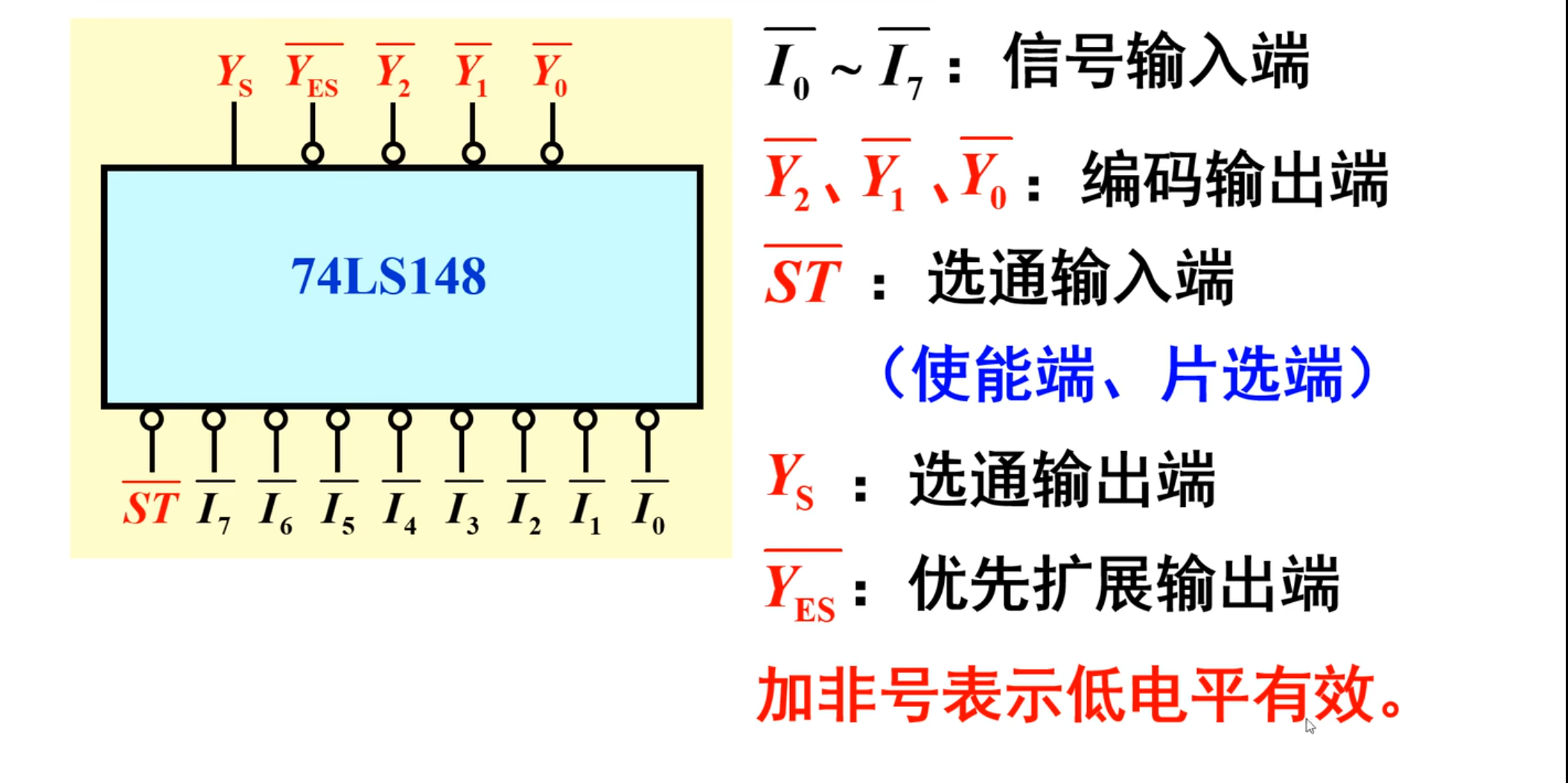
74 LS 148 优先编码器

这里就不再是传统的门电路了，而是下面这种集成电路：

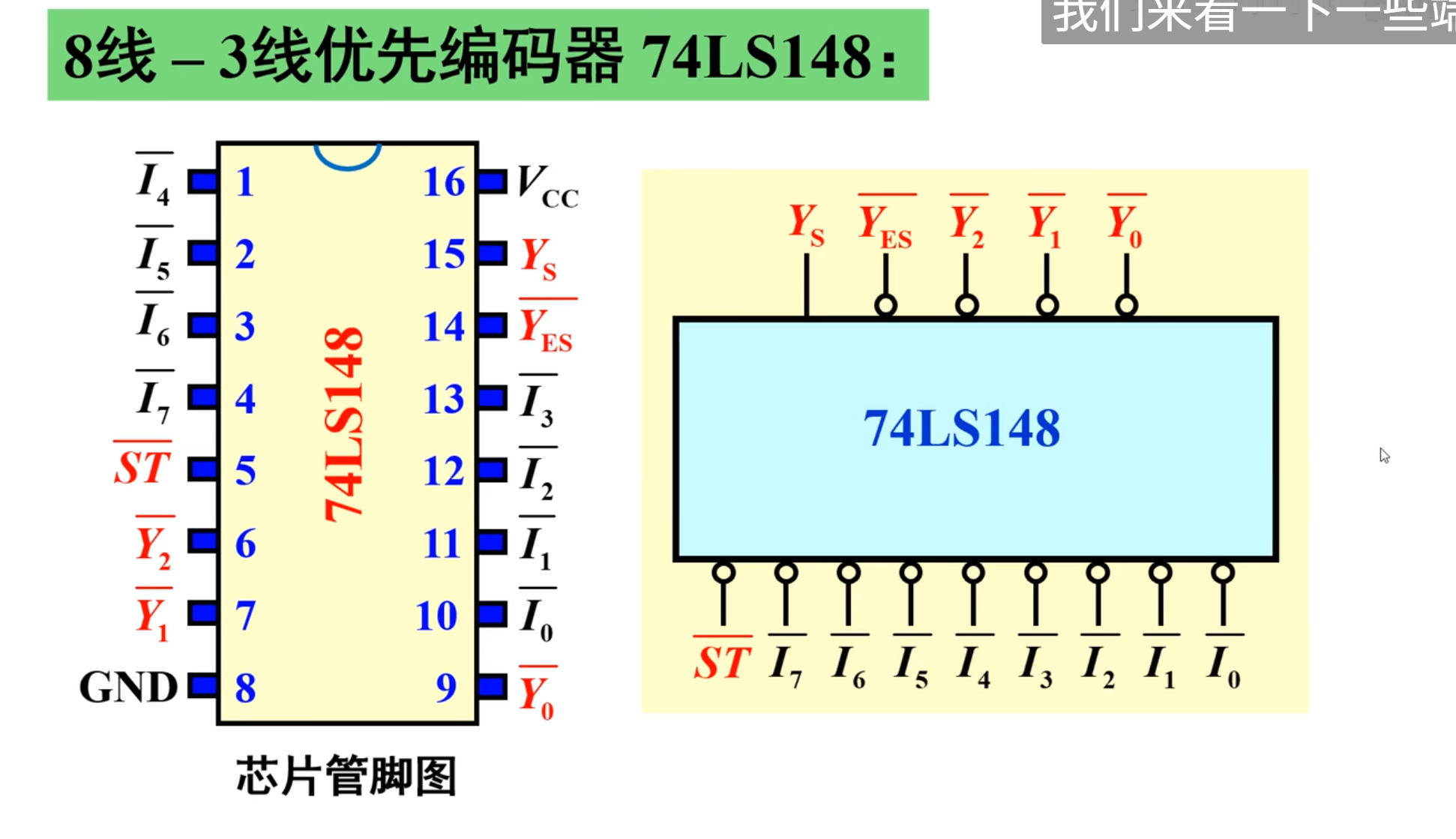
右边的是示意图。

下面对引脚进行说明：

下面是功能表：

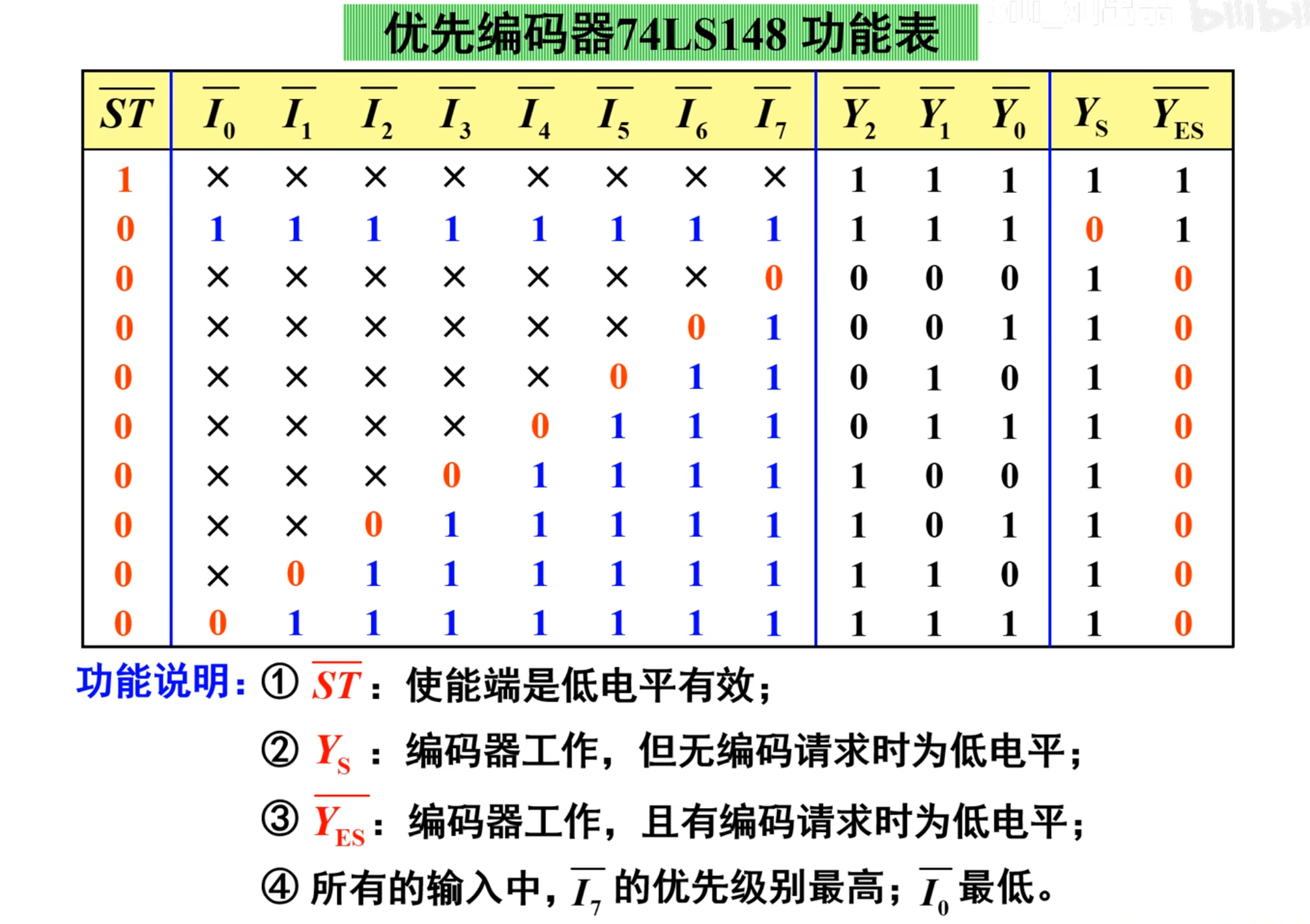
当 $\overline{ST}$ 为 1 的时候，代表不工作，所以无论输入是什么，输出都是 1

只有当 $\overline{ST}$ 为 0 的时候，代表工作，才能进行编码。

而第二行都是 1，代表没有一个信号有效（没有信号输入），因为这里是低电平有效，所以，全 1 其实是全 0

当 $\overline{ST}$ 为 0 代表工作的时候， $Y_s$ 和 $\overline{Y_{ES}}$ 则相反的。

当输入无效的时候（输入全是 0，取反之后为全 1）， $Y_s$ 为 0， $\overline{Y_{ES}}$ 为 1。

从上面图中的第三行开始则是正常进行编码

---

下面是 CD 4532 的功能表

其功能于 148 一样，唯一不同不就是这个是高电平有效，148 是低电平有效

其中的 $GS$ 是判断是否有输入的，如果芯片没有输入或者输入使能端为 $0$ ，那么 $GS$ 的输出也是 $0$

$EI$ 代表的是输入使能端，当它为 $0$ 的时候，相当于芯片没有启动，无论输入如何，其功能相当于无作用。

$EO$ 代表输出使能端，当芯片有输出的时候， $EO$ 为 $0$ ，反之，当芯片启动并且没有输入的时候， $EO$ 为 $1$

148 级联成 16-4 优先编码器

首先来看级联之后的真值表：

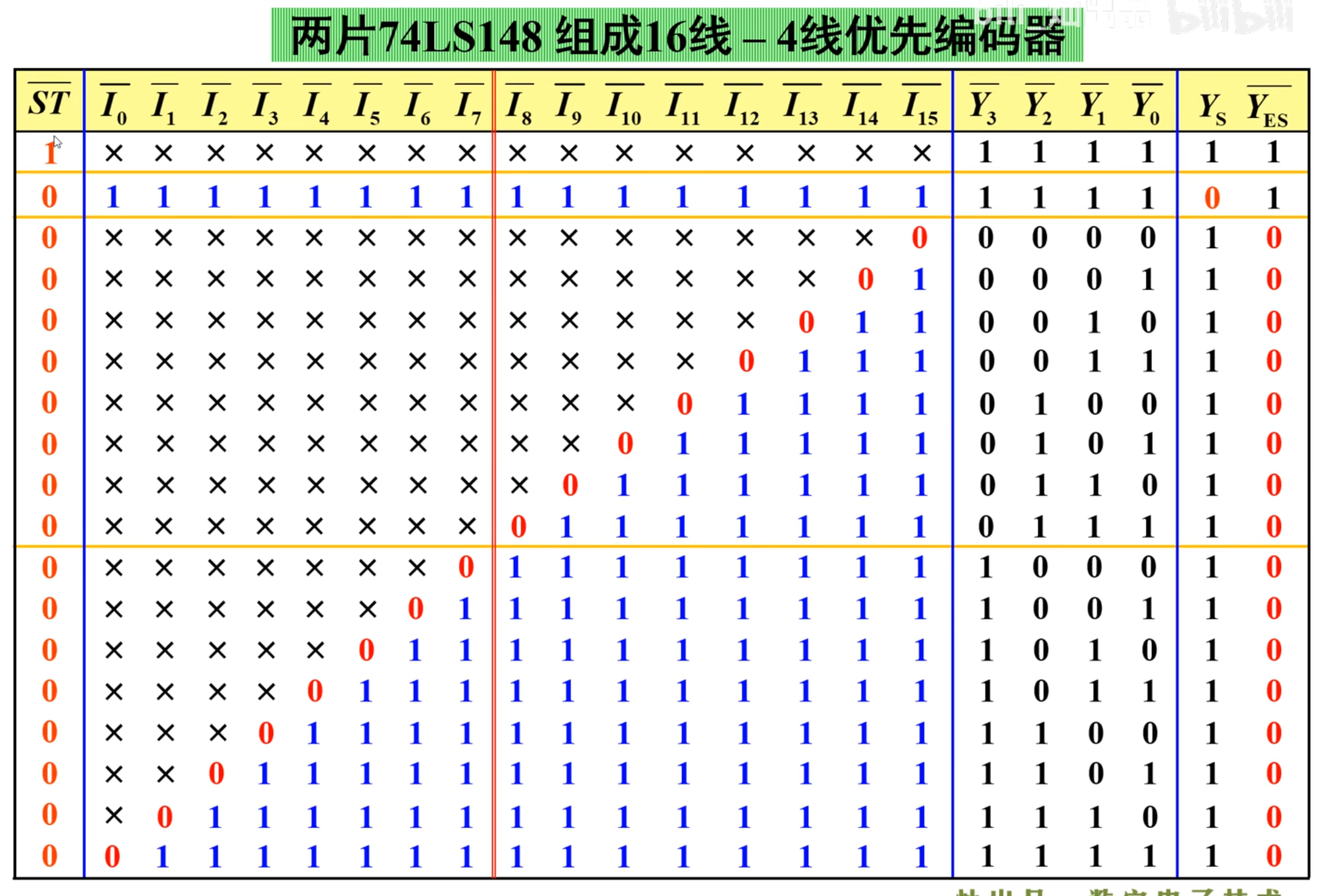
在上面图中，中间红线左边是低位的 148，右边是高位的 148，问题在于如何将这两部分连接到一起，实现功能。

注意看真值表，当高位片工作的时候，低位片是不工作的，所以，将高位片的 $Y_S$ 连接到低位片的 $\overline{ST}$ 上。

此外，无论是高位片还是低位片，都是只有 $\overline{Y_2}$ 、 $\overline{Y_1}$ 、 $\overline{Y_0}$ 的，没有 $\overline{Y_3}$ 的，我们需要找一个地方来当做 $\overline{Y_3}$

然后，当低位片工作的时候，高位片也是不能工作的。

所以，可以发现，最终输出的 $\overline{Y_3}$ 与高位片的 $\overline{Y_{ES}}$ 之间有些许关联。

而最终输出的 $\overline{Y_0}$ 、 $\overline{Y_1}$ 、 $\overline{Y_2}$ ，与高位片和低位片之间的输出的关系是与

进而得到最后的电路图：

---

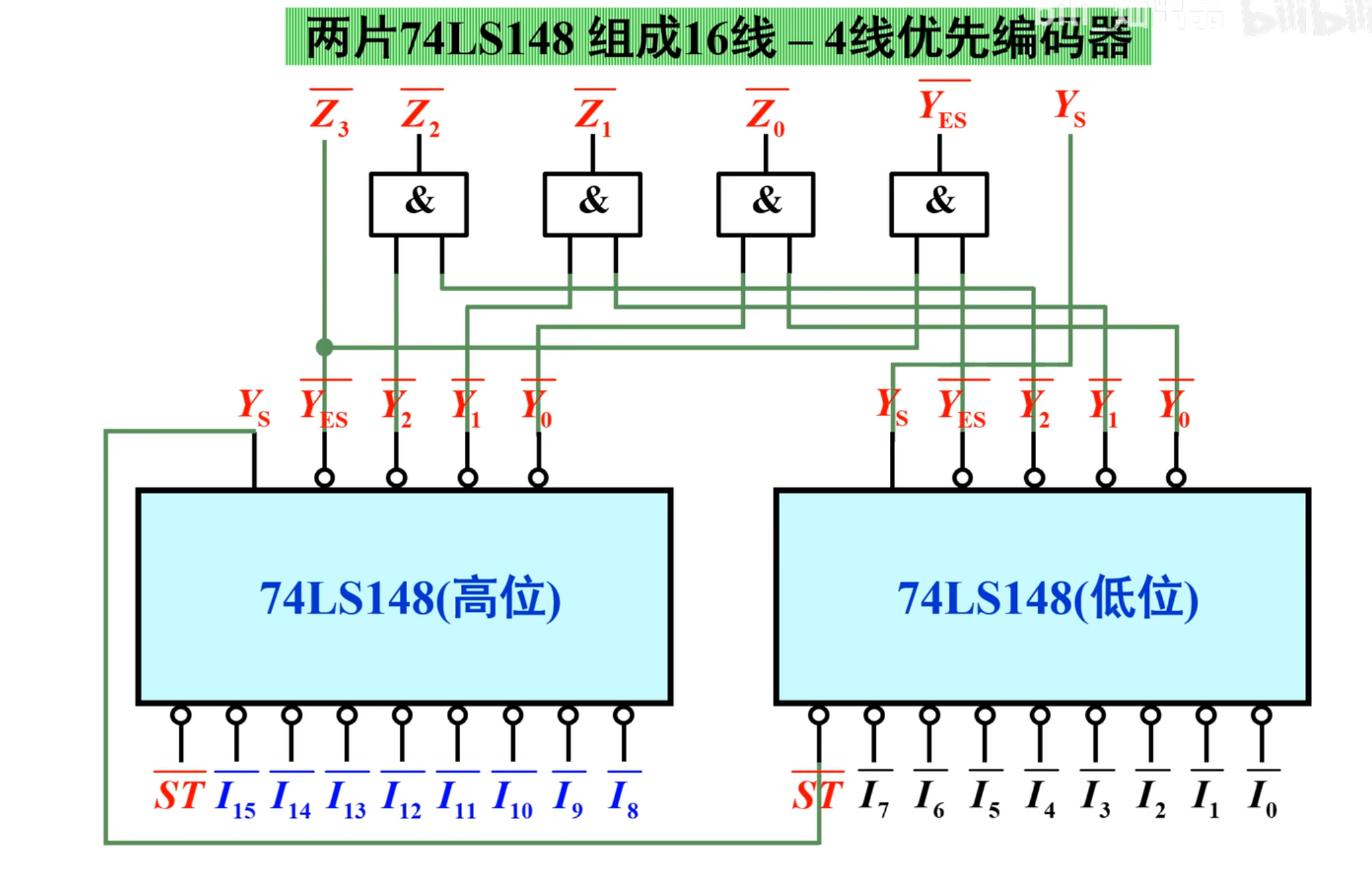
补充关于 CD 4532 级联的功能示意。

同样的，与 148 功能相同，区别在于高低位激活不一样。

唯一需要注意的是，最后输出四位中的最高位是高位芯片的使能端，原因在于当高位有输入的时候，最高位肯定是 $1$ ，而当高位芯片没有输入，但低位芯片有输入的时候，高位芯片的使能端肯定是 $0$ ，这也就保证了输出的正确性。

十 - 四优先编码器 147

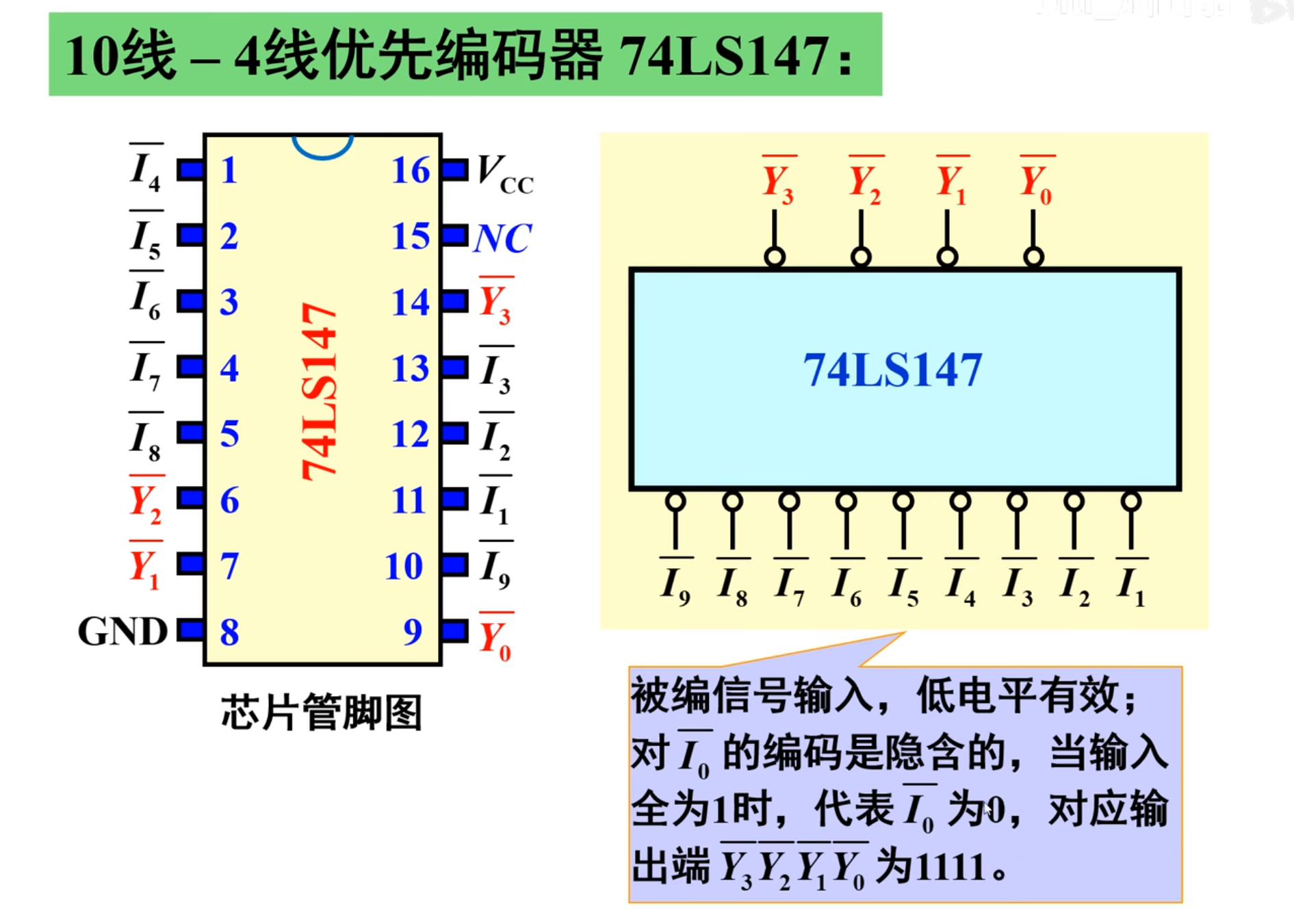
这个芯片比较特殊，尽管是十位转四位，但是对 $\overline{I_0}$ 的编码是隐藏的，当输入端全为 1 的时候，代表 $\overline{I_0}$ 为 0，对应的输出是 $1111$

下面是功能（真值）表

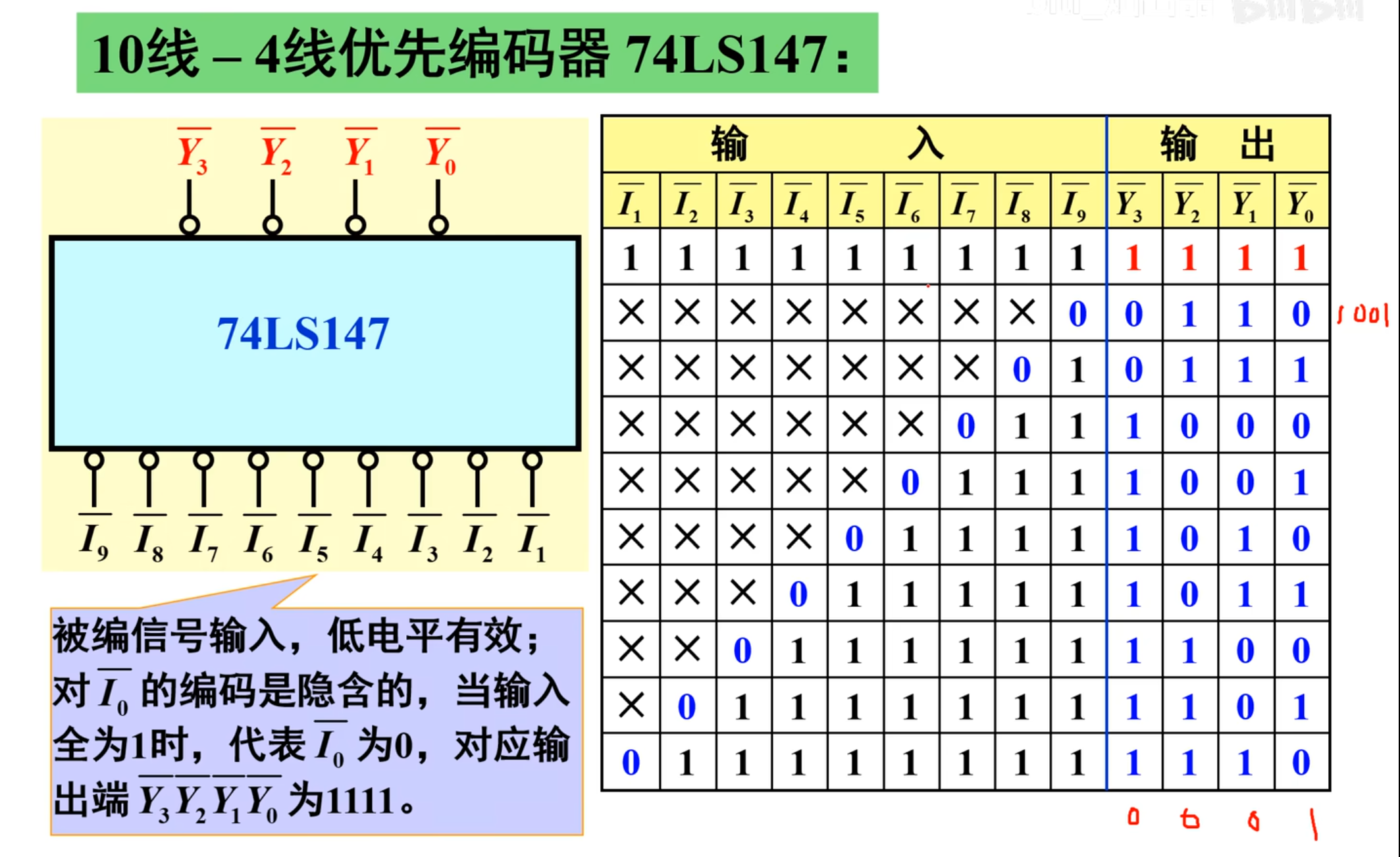
需要注意到是，这个的编码是反码，首先来看第二行，代表的是 9，而 9 的二进制是 1001，而取反之后得到的是 0110.

其他的也是以此类推。

至于说最上面的哪个全 1 输入，得到的结果是 1111，而取反之后得到的是 0000，代表的也是 0.

IMPORTANT

上面的这部分关于级联编码器以及十-四优先编码器，后续如果有需要再去看。 -- 2025 年 5 月 5 日

译码器

译码器与编码器可以说是相反作用的两个器件。

译码：将具有特定意义的二进制代码转换成相应信号输出的过程。

译码器将二进制代码转换成相应信号输出的时候只能译出来一个有效电平。

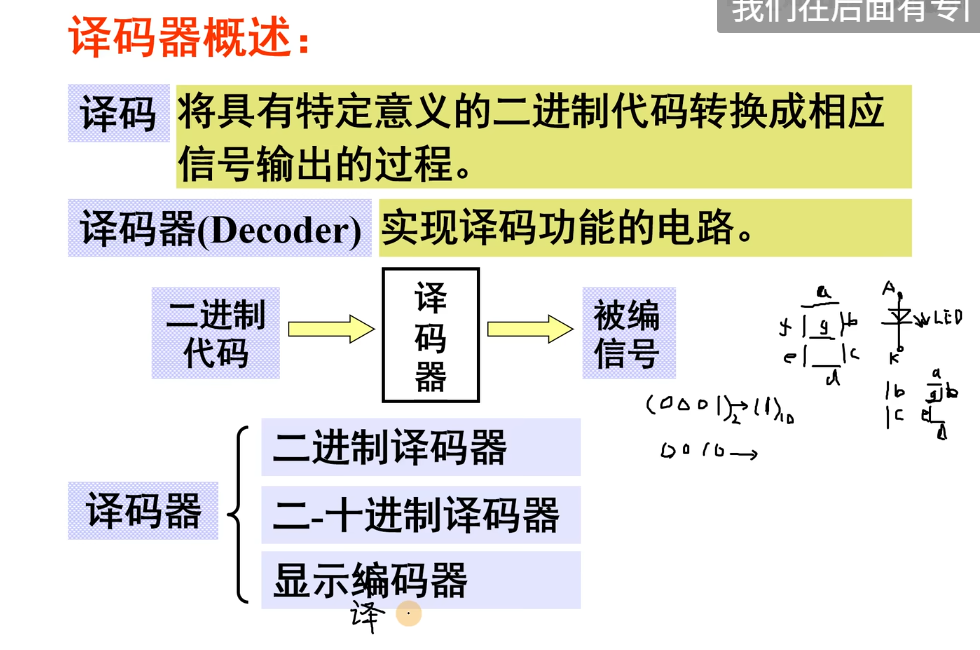
二进制译码器

将输入二进制代码的各种组合按照其原意转换成对应信号输出的逻辑电路

还是以一个例子的方法来说明：

设输入 3 位二进制代码为 $A_2$ 、 $A_1$ 、 $A_0$ ，共有 $2^3=8$ 种不同组合。它有 8 个输出端，用 $Y_0$ 、 $Y_1$ 、 $\cdots$ 、 $Y_7$ 来表示，输出高电平 1 有效

下面列出其功能表（真值表）

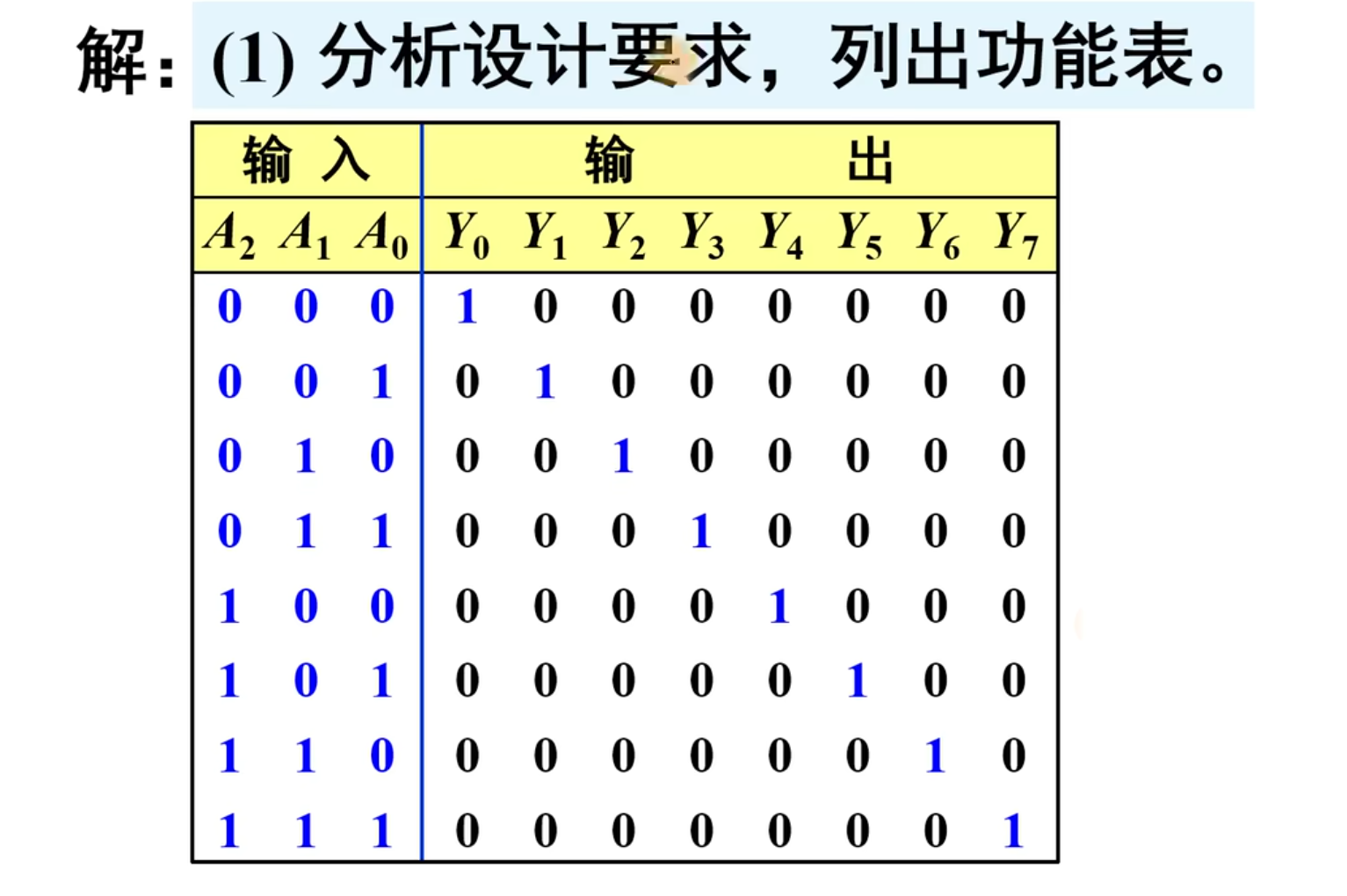
然后是写出逻辑函数表达式：

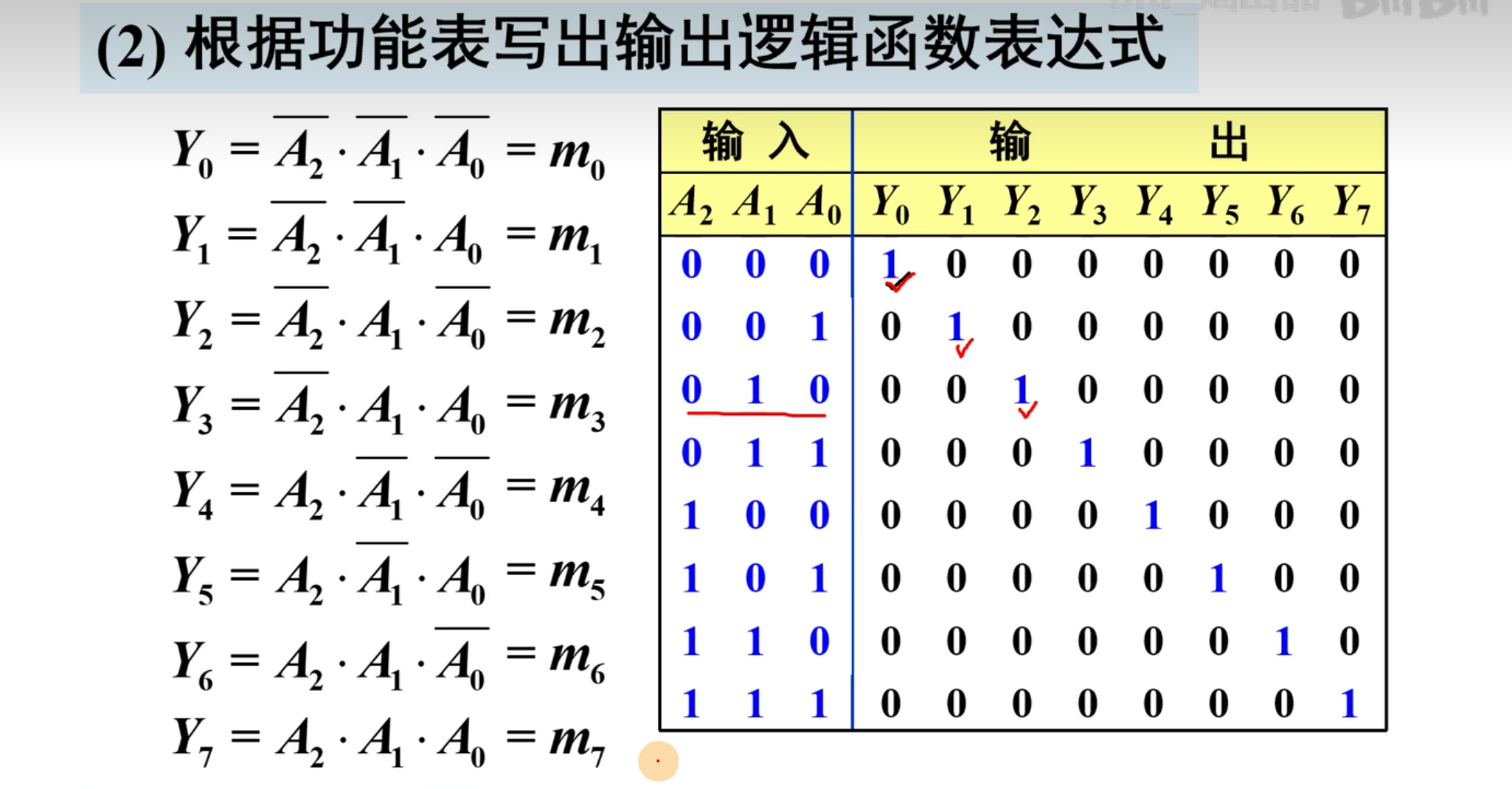
可以发现其中，每一个输出 $Y_i$ 都是一个最小项，（只包含自身和自身的反）

如果我们用这些最小项进行组合，就可以得到其他的逻辑函数，比如只把前四项或到一起

如果把这些最小项做一个组合，那么就可以构成三个变量的任意逻辑函数

所以，二进制译码器也称为函数发生器。

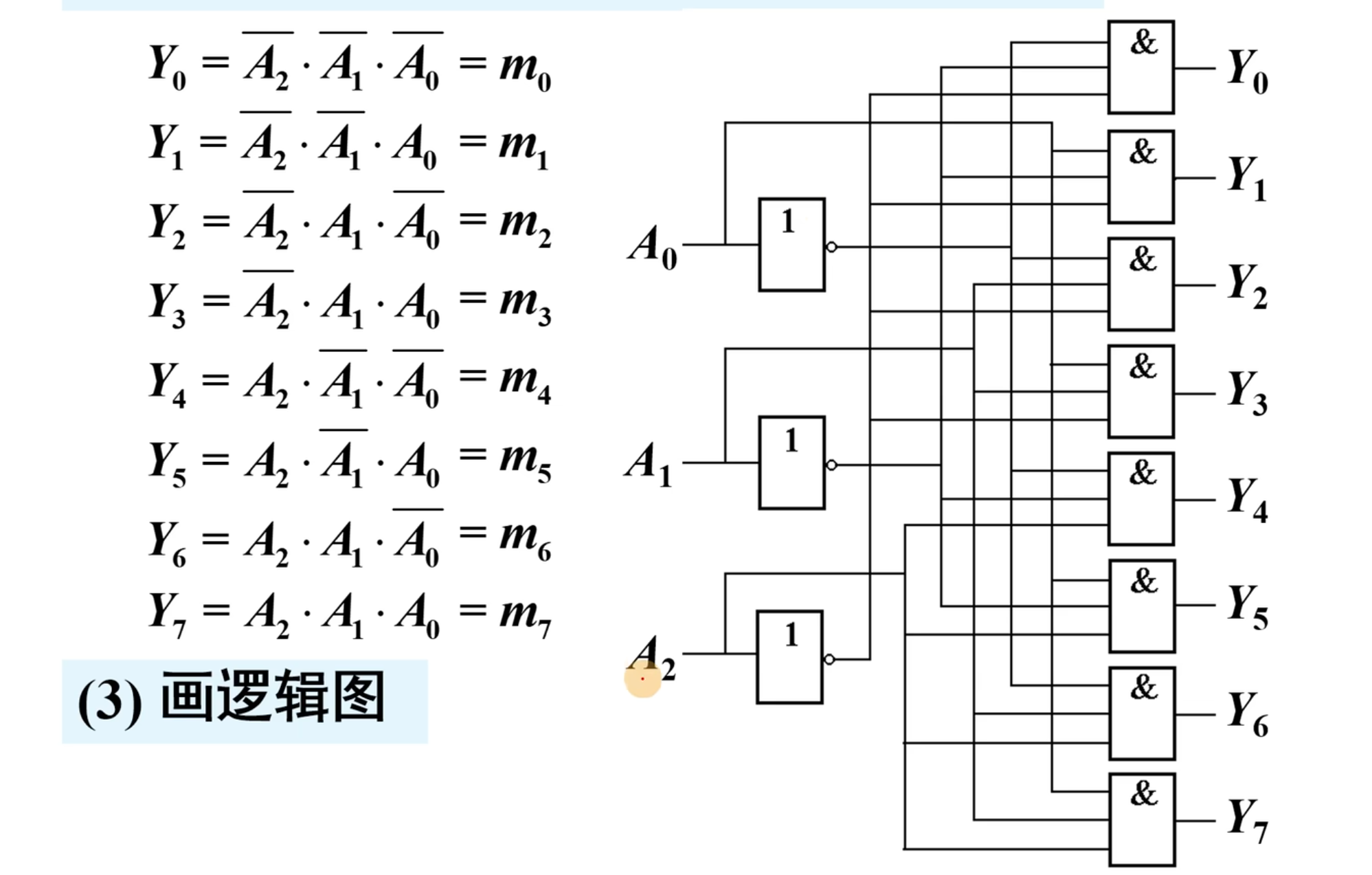
接下来画一下逻辑图：

双 2 线-4 线译码器 139

这一部分使用的比较少。

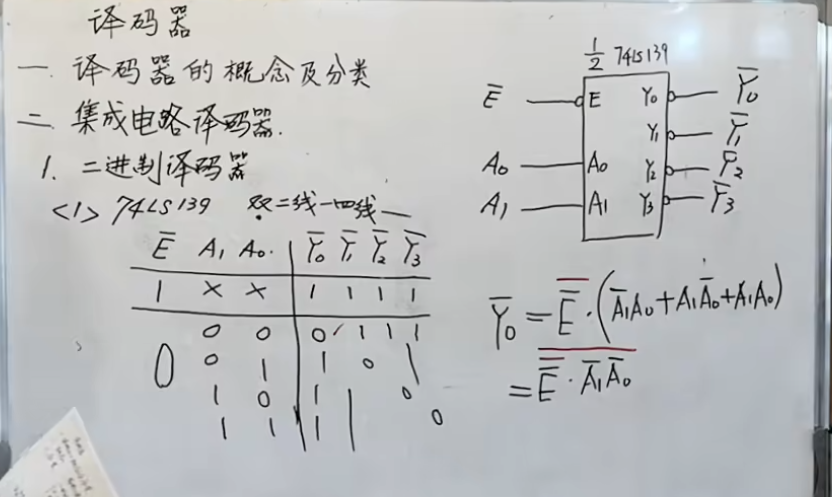
这里是低电平有效，所以上面的使能端和输出都是以低电平的形式输出。

当使能端 $\bar{E}=1$ 的时候，代表芯片不工作，所以无论输入如何，其输出都为 1

反之，当使能端为 0 的时候，意味着开始工作。

NOTE

需要注意的是，这个是译码器，所以在输出的时候，每一位输出都只能有一位有效。（因为是低电平有效，所以以 $0$ 代表有效 ）

在图中使用了逻辑表达式的方法来表示 $\overline{Y_0}$ ，当然可以使用卡诺图的方法将其写出来。

3 线 - 8 线译码器 138

这个译码器是一个非常通用的一个译码器

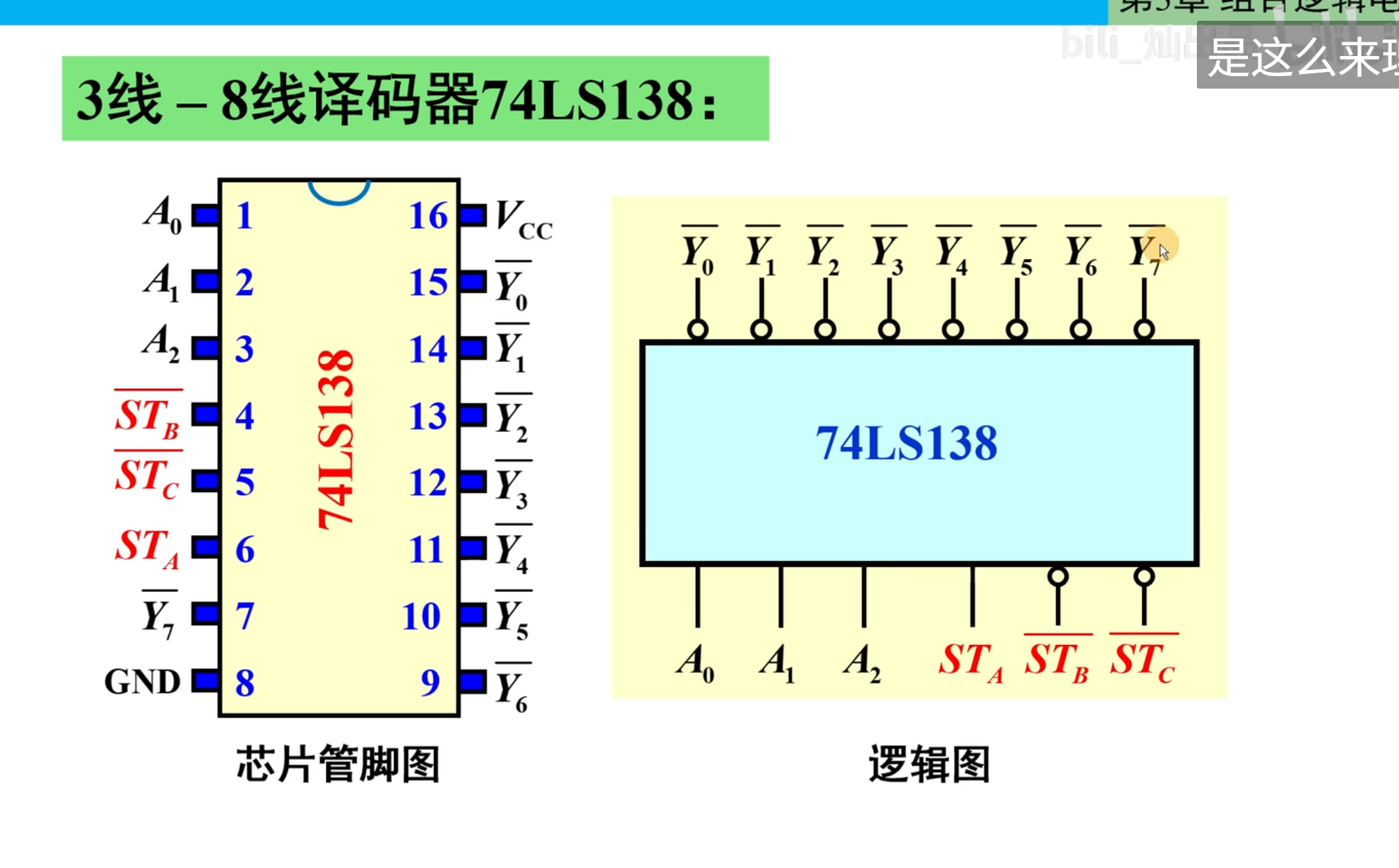
下面对引脚进行说明：

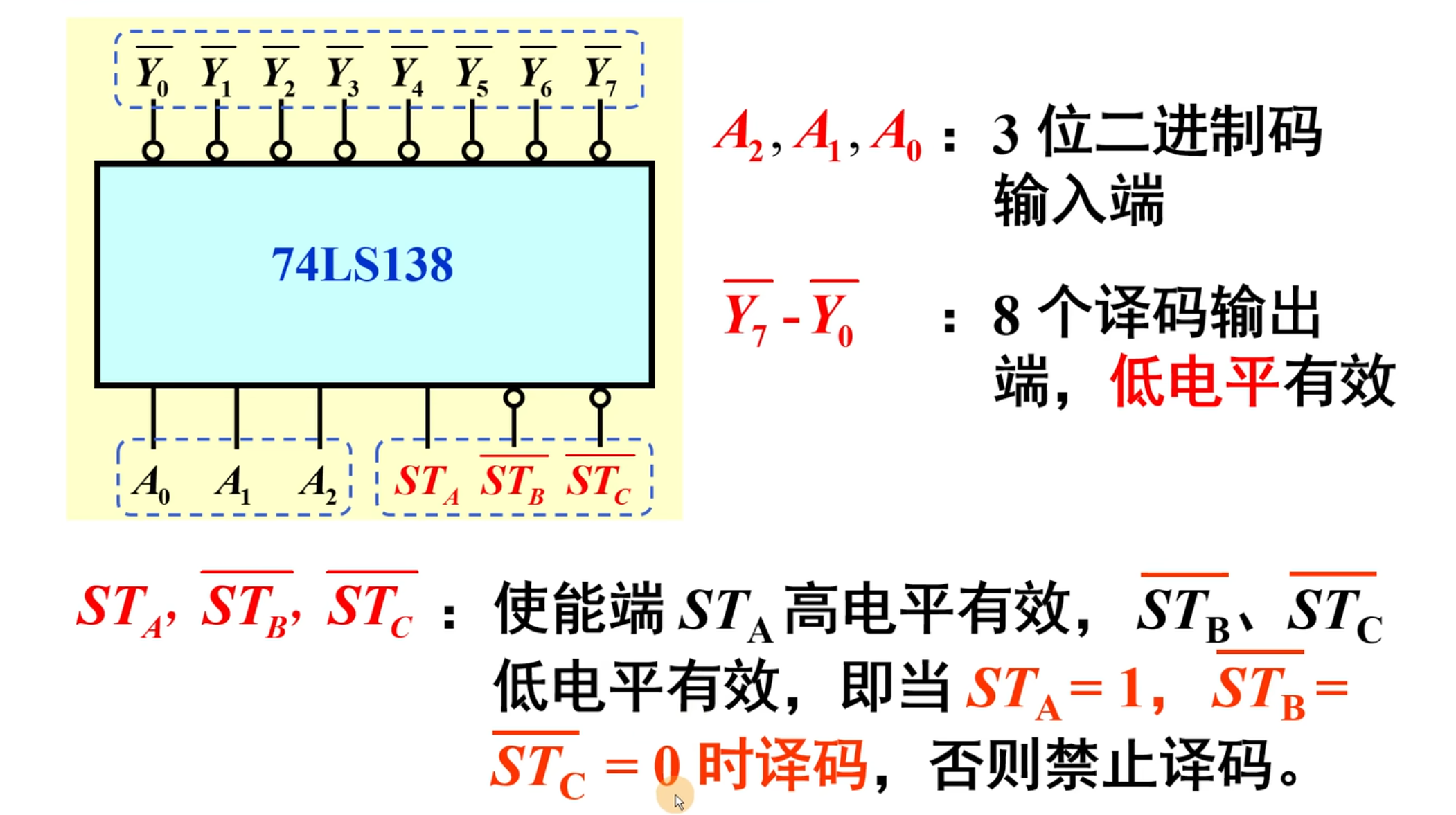
只有当 $S{T}_A=1$ 、 $\overline{S{T}_B}=\overline{S{T}_C}=0$ 的时候才进行译码，否则不进行译码，不进行译码输出的结果就是全 0

下面是其功能表（真值表）

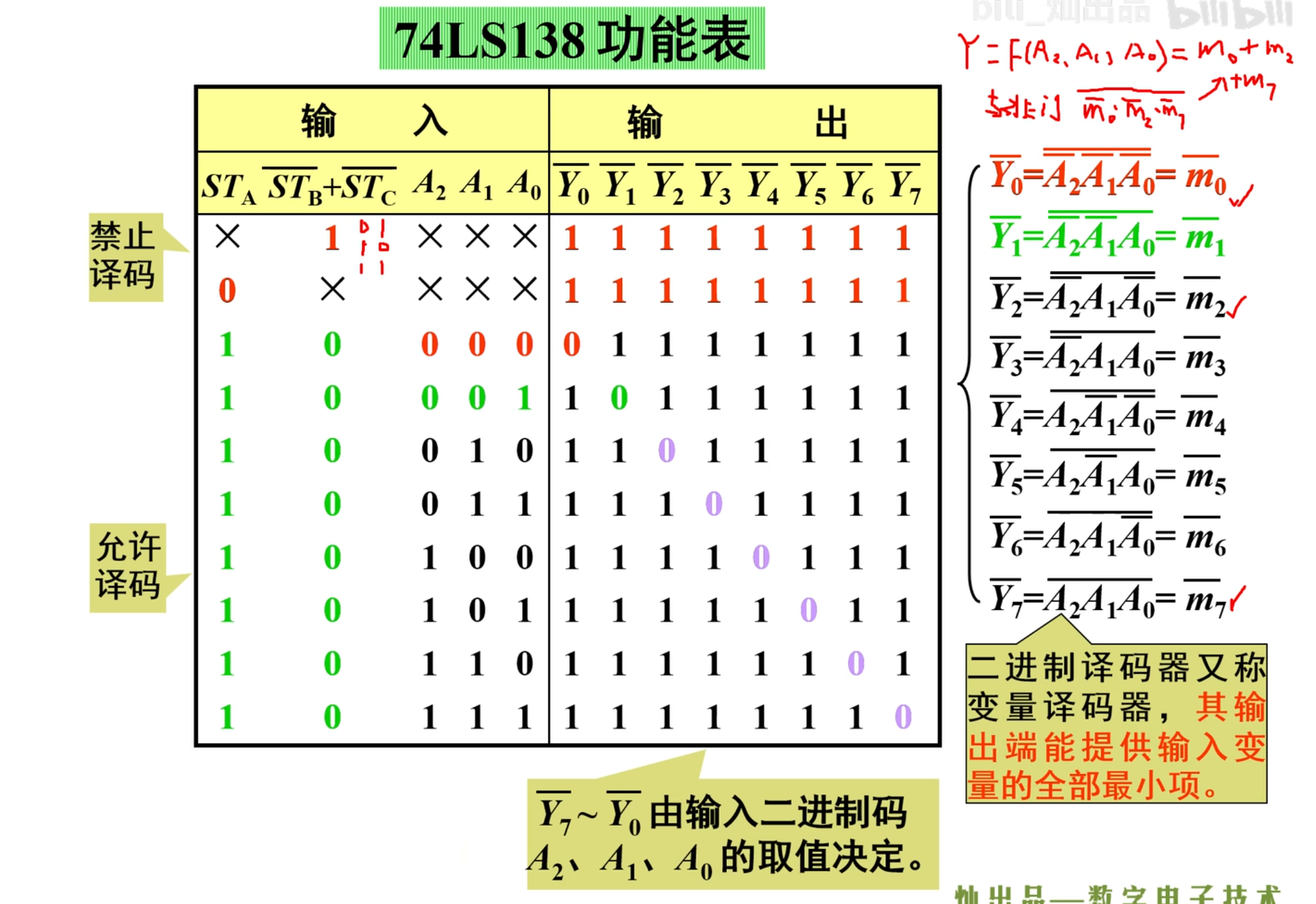
需要注意的是，由于最后的输出都加上了一个非，所以在进行最后的函数上的逻辑运算的时候，要用与非门来实现逻辑组合，原因在于 $\overline{\stackrel{―}{m_0}\cdot \stackrel{―}{m_1}\cdot \stackrel{―}{m_2}}=m_0+m_1+m_2$

下面对上面的功能表做一个补充：

只有当 $E_3$ 、 $\overline{E_2}$ 、 $\overline{E_1}$ 的顺序依次为 $100$ 的时候，译码器才会工作，其他情况下都不会工作。不会工作的状态有七种。

同时，在输出端，依然是只有一种输出。

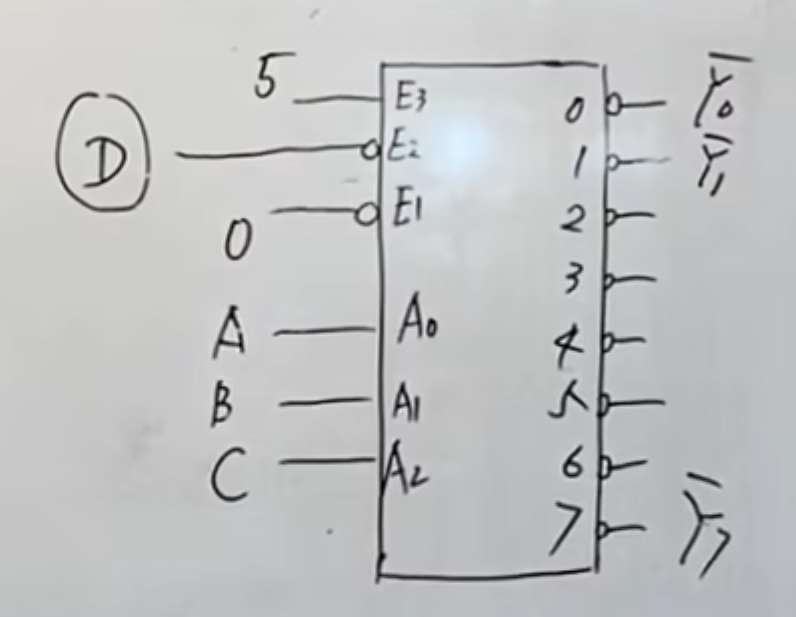
3 线 - 8 线译码器的应用

已知输入波形画出输出

这个时候，一般是 $E_3$ 接入 $5v$ ， $\overline{E_1}$ 接地，也就是 $0v$

控制器由 $E_2$ 来控制。

具体的例子如下图：

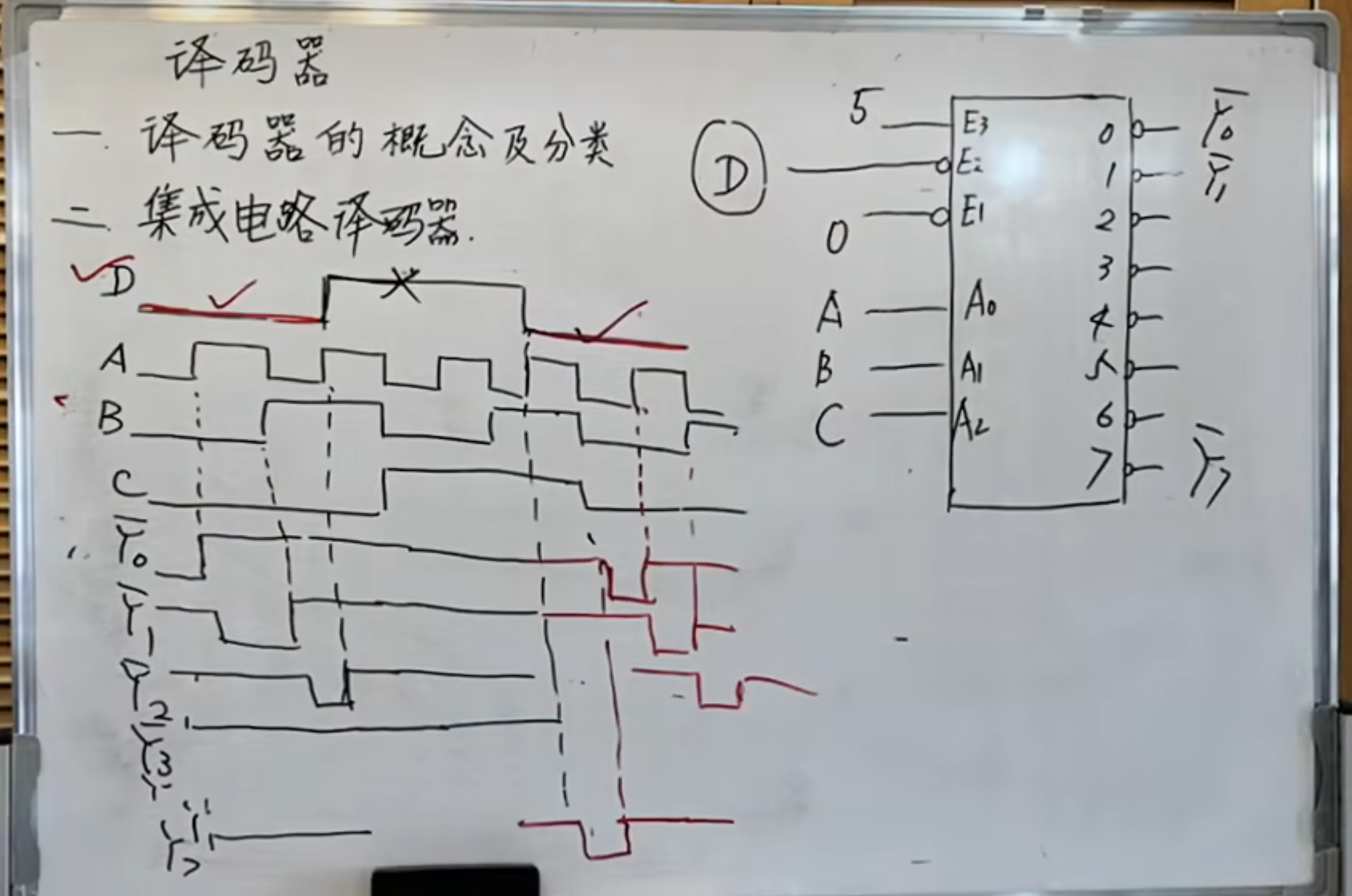
138 译码器的扩展

有的时候，一片 138 译码器不够用，需要两个 138 译码器组成 4-16 译码器

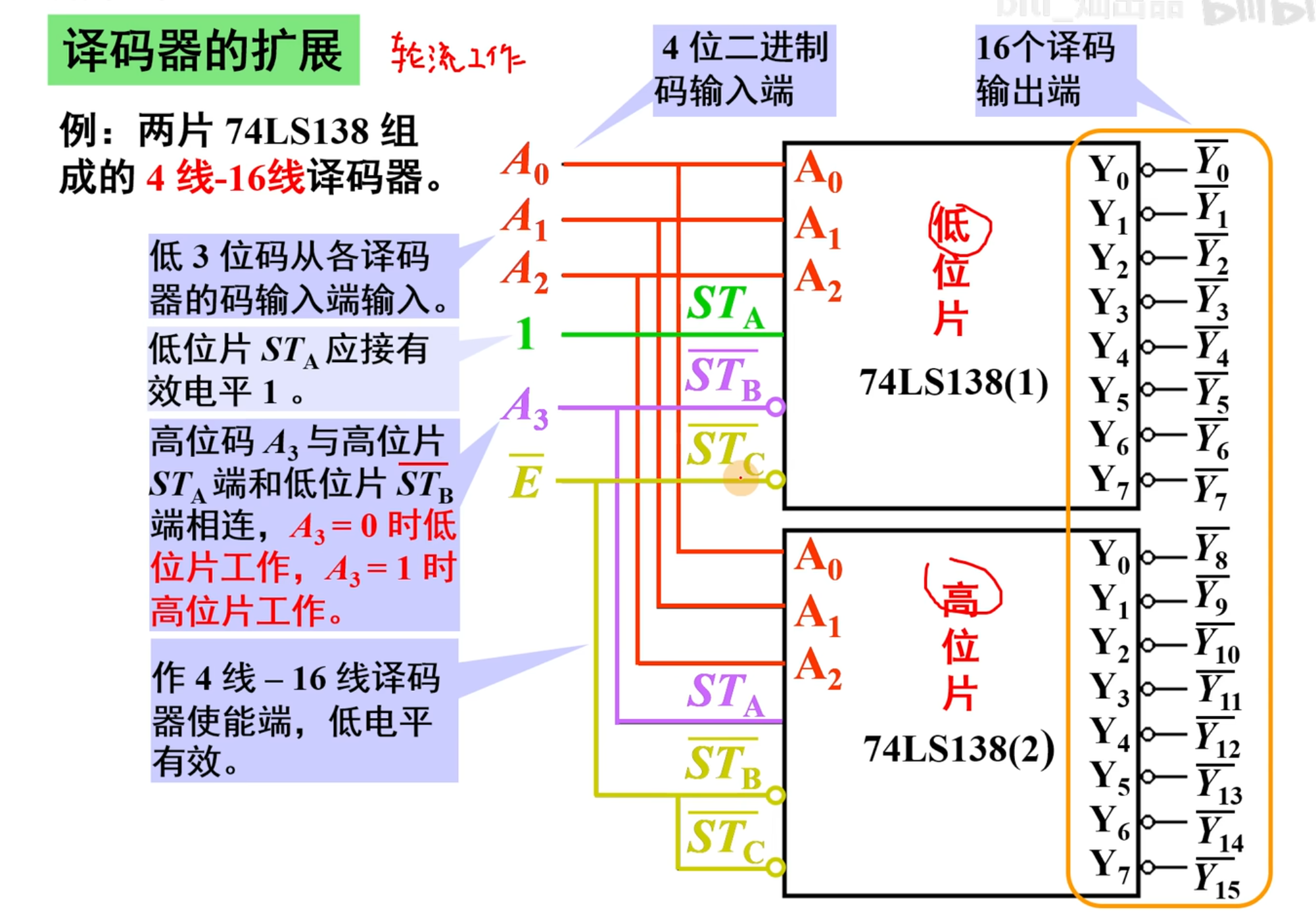
注意看上图中，利用芯片 $S{T}_A$ 的特性，将其设置为最高位，当 $A_3=0$ 的时候，低位片工作，当 $A_3=1$ 的时候，高位片工作。

下面详细解释一下工作原理

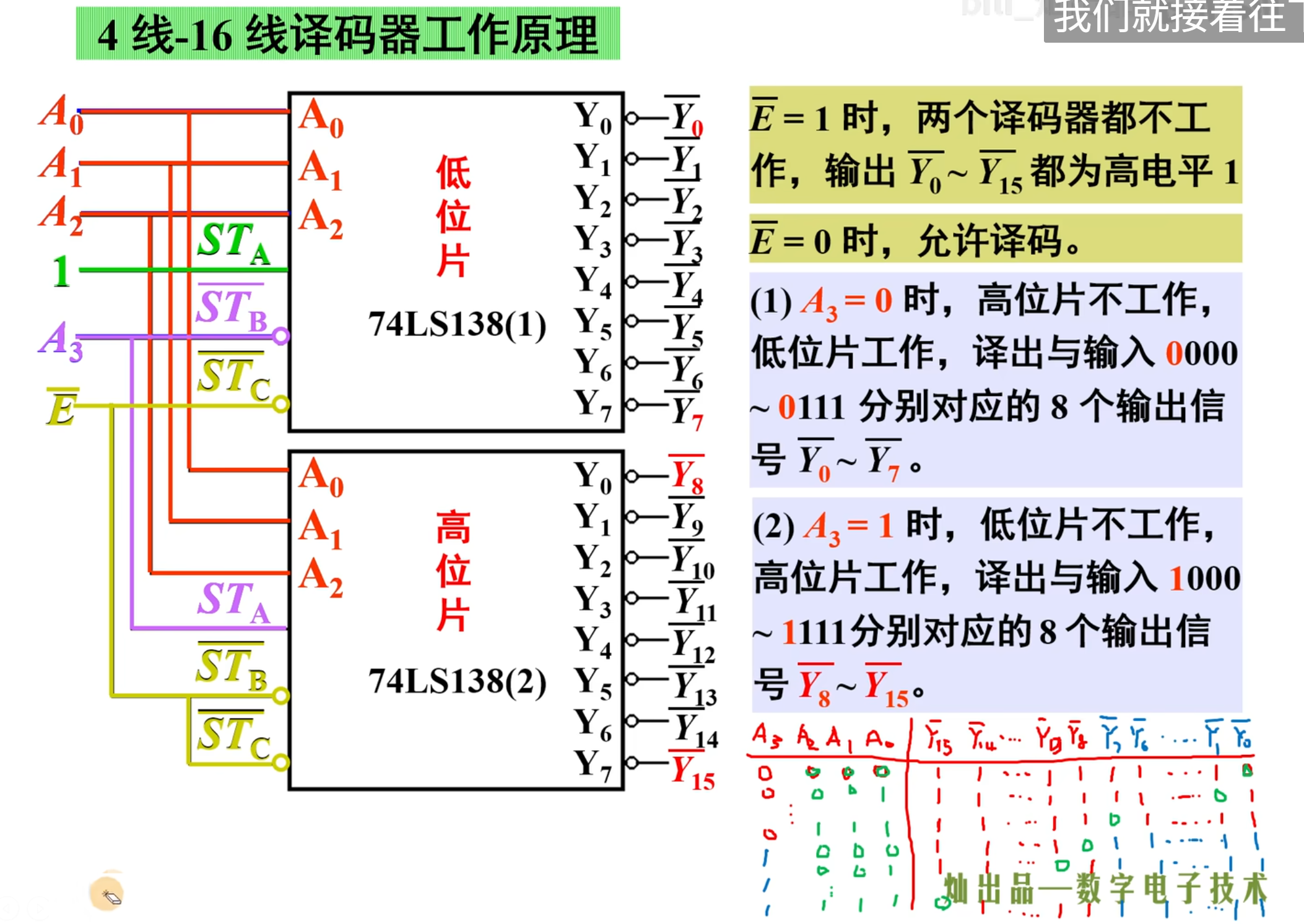
注意看上面图中右下角的表，这个表就是其实现的效果。

下面进行补充：

将译码器扩展到 $5$ 线 $32$ 线译码器。

这个是四片 138 联合起来

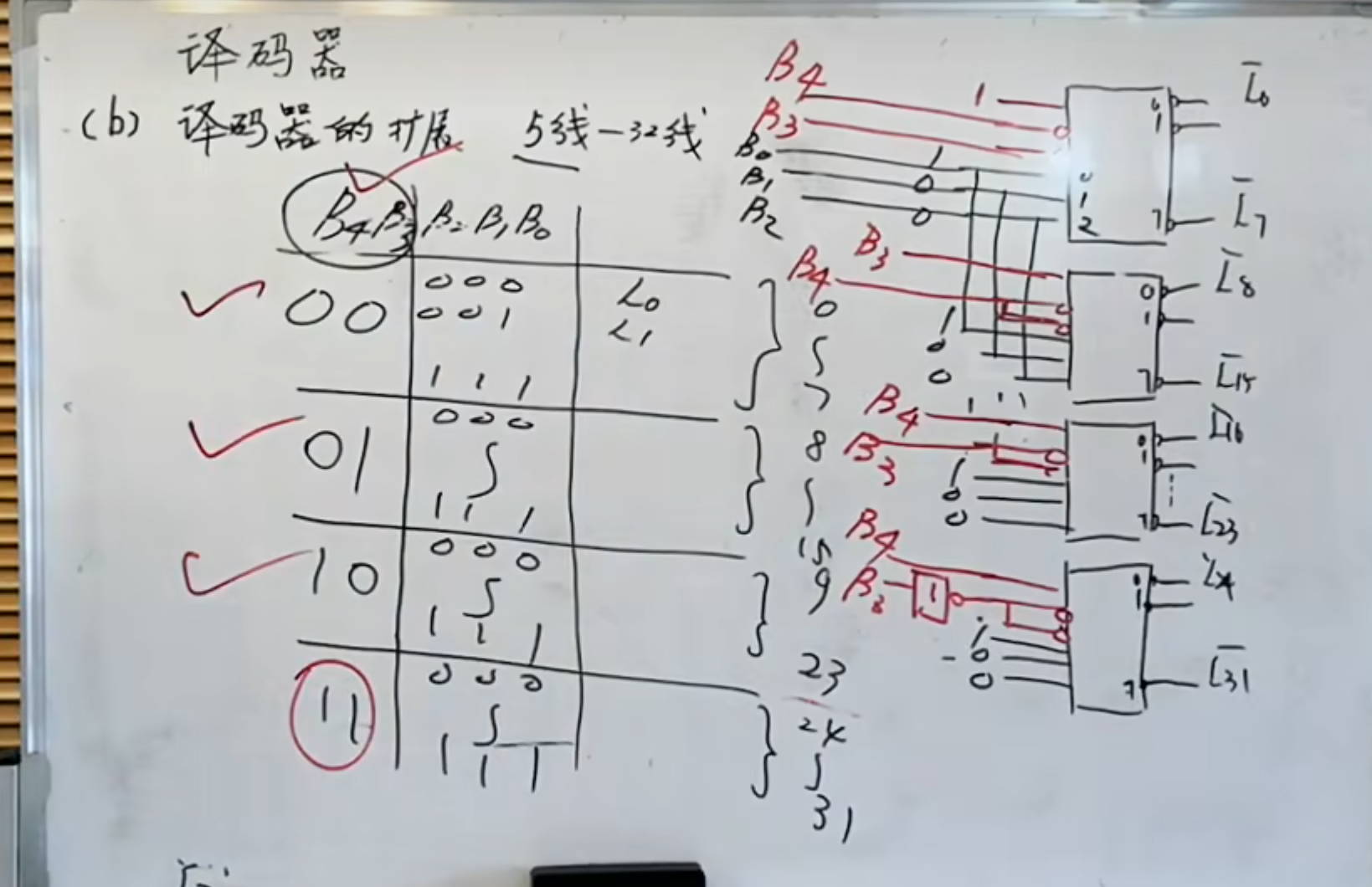
首先来分析功能表，一共有五位输入，32 位输出。

可以发现后三位是以 8 位一组为循环。所以，我们按顺序将后三位连接到每一个芯片的三位数据输入端上。

之所以是每一片，原因在于前两位的输入。

前两位的连接方法如上面图中所示，按照从高位到低位的特点进行连接。

这个方法主要是利用控制使能端的方法对从高位到低位各个芯片的控制，让其能够输出正确的顺序。

举个例子既可以理解：

假设输入的是 $B_4{B}_3{B}_2{B}_1{B}_0=10011$

首先看后三位，是 $011$ ，当被输入的时候，每一个芯片上的三位输入，输入的都是 $011$

如果使能端都是正常工作的，那么每一个芯片的输出都是 $\overline{L_3}$ （第三位）

但是前面两位就需要通过控制每个使能端的方法来保证其输出是正确的。

由于输入是 $10$ ，利用图中的连接方法，第一个连接的方式得到的结果是 $110$ ，很明显，此芯片是不工作的，其输出就变成了全是 0

其他的以此类推。只有当芯片的使能端满足 $100$ 的方法才能保持工作。

---

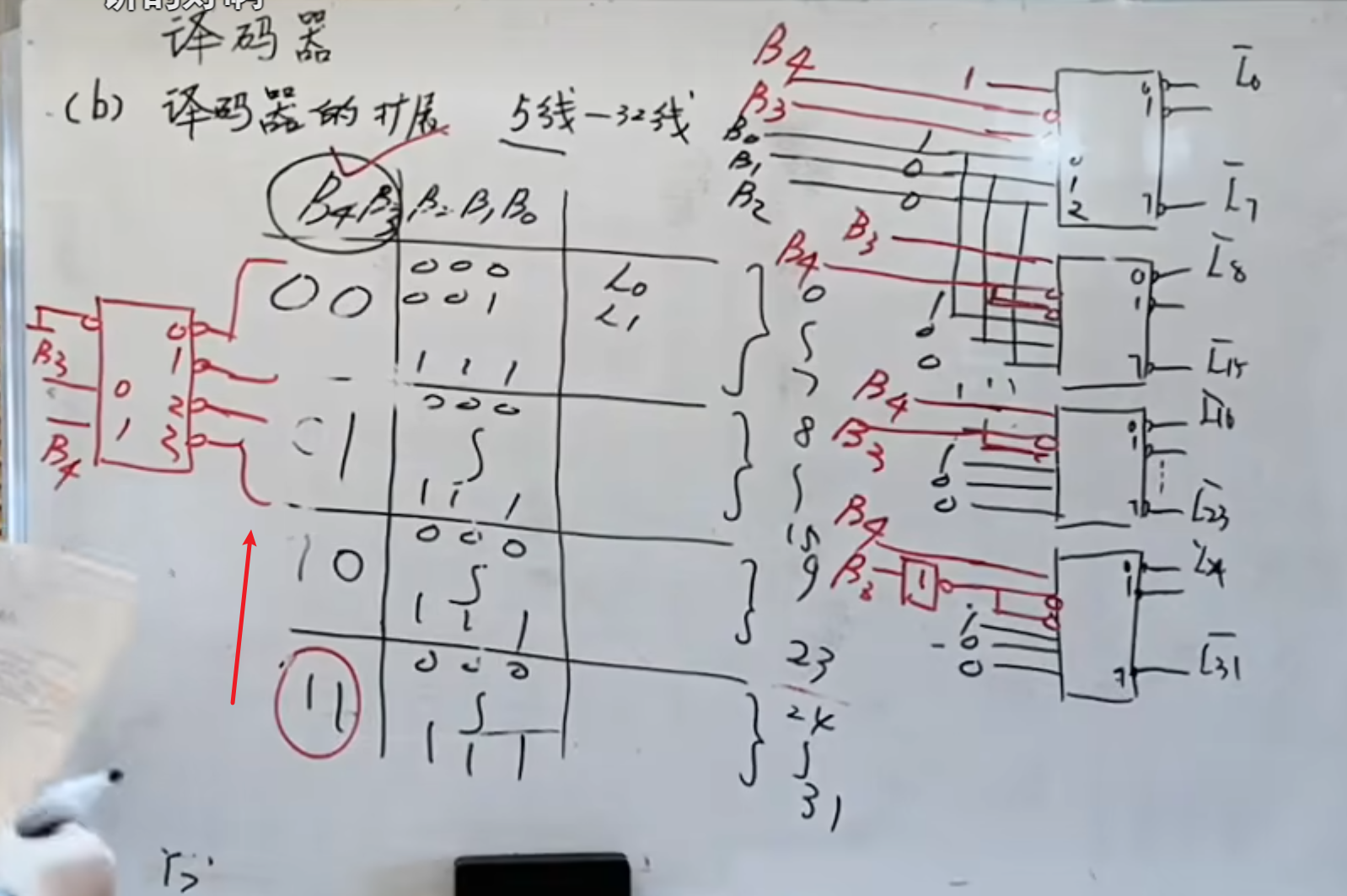
当然，还可以使用将前面两位（高位）的输入利用 139 译码器（2 线 - 4 线译码器），将其输出连接到每个芯片使能端的低电位（两个）

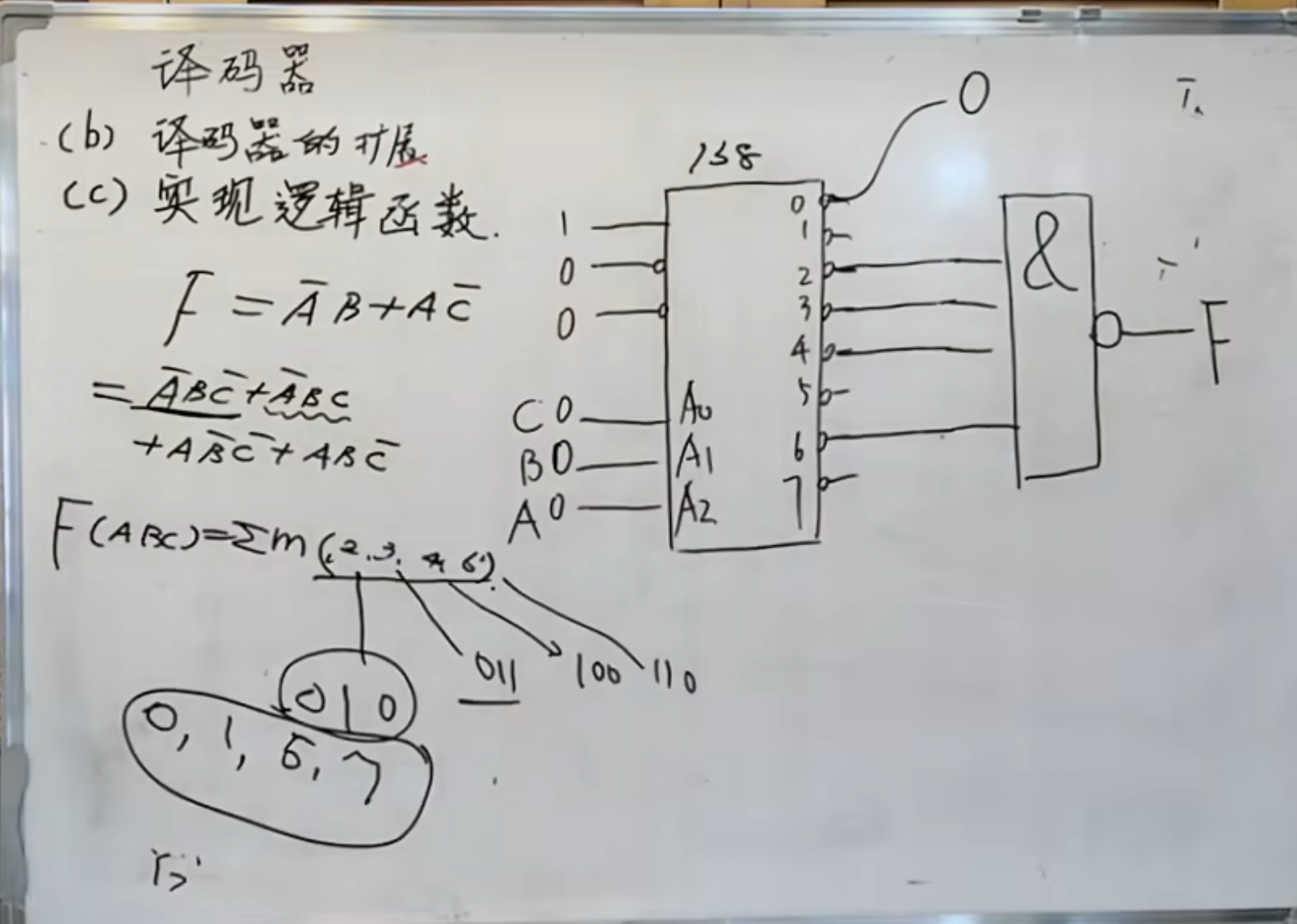
译码器实现逻辑函数

用例子来实现：

$$F=\bar{A}B+A\bar{C}$$

首先是将逻辑函数换成最小项。

可以使用公式来计算，也可以使用卡诺图的方法得到最小项。

$$F(A,B,B)=\sum m(2,3,4,6)$$

然后是使用 138 来进行表达。

很明显，将 $ABC$ 按照顺序将其连接到 138 的输入上。当输入为 $011$ 的时候，经过译码器，译码器的 $\overline{L_3}$ 相应，输出为 $0$

同样的，每一个最小项的输入都会有一个对应的输出。但是，最后的结果与相应的是相反的。

所以要将所有最小项输出相应通过一个与非门连接起来，就能得到最后的结果

---

扩展情况：

由于一个 138 译码器的正常输入是三位的，但如果想要输入一个 4 位的逻辑函数，如何使用译码器实现逻辑函数

可以使用两片 138 译码器连接到一起来实现这个功能。

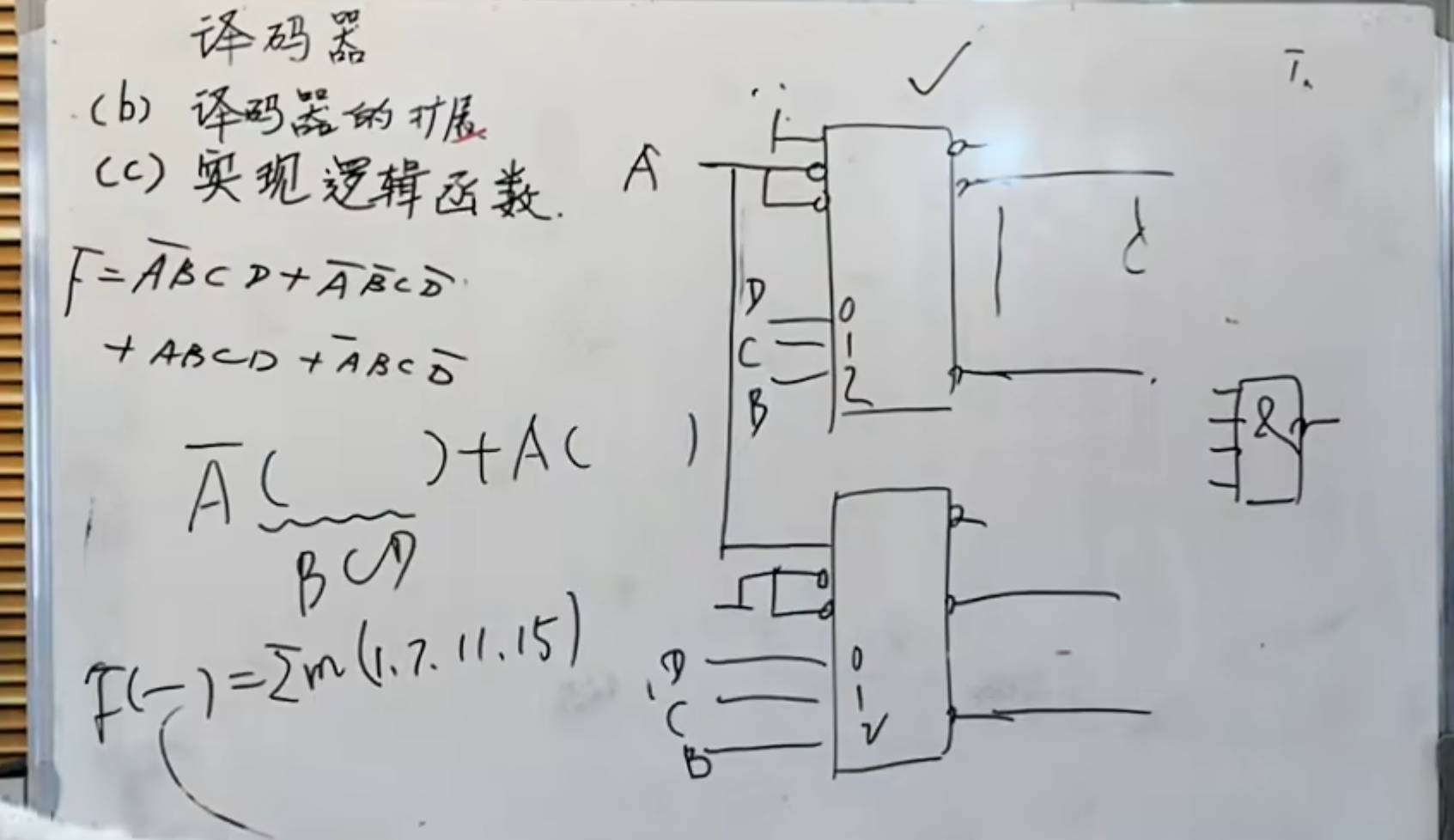
这里的主要思想是将最高位的作用设置为控制使能端，然后将剩下的三位按顺序连接到每个 138 的输入端上。

最高位在控制使能端的时候，低位的芯片与高位的芯片在连接上有所不同，一般来说，是将 A 连接到低位的低控制端上，并且连接到高位的高控制端上。这样，当 $A=1$ 的时候，就能让低位不工作。只让高位工作。当 $A=0$ 的时候，让低位工作，让高位不工作。

这样的思想其实是将高位、低位两篇芯片的每一个输出都有对应。将所以的可能性分成两部分，也就是 $F_{all}=\bar{A}(BCD)+A(BCD)$

当然最后的输出还是使用与非门将其连接起来。

---

在实现上面的功能的时候还有一种更简便的方法（更巧妙的方法）

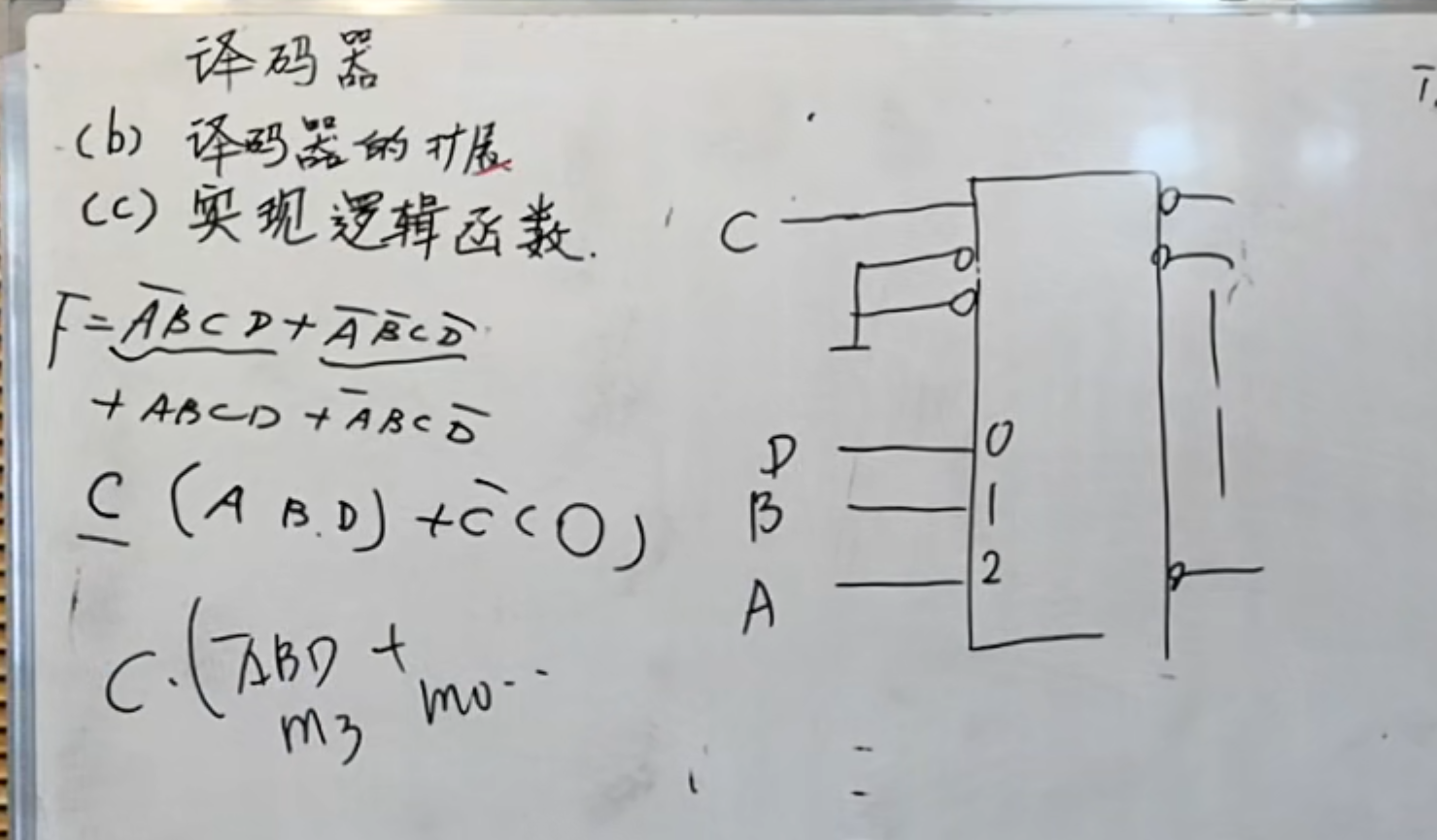
观察这个函数，这个函数可以化成 $F=C(ABD)+\bar{C}\cdot 0$ 的形式，那么就不需要两个 138 译码器了。

但是需要注意的是，译码器的输入端三个变量的连接顺序需要有所变化。

$$F=C\cdot (\bar{A}BD+\bar{A}\cdot \bar{B}\cdot \bar{D}+ABD+\bar{A}B\bar{D})=C\cdot (m_3+m_0+m_7+m_2)$$

当然，因为在给定的逻辑表达式中， $C$ 一直都是 $1$ 的，所以直接将 $C$ 连接到使能端的高电平端即可使译码器工作。

138 组成数据分配器

首先理解什么是数据分配器：将一个信号输入进来，然后找到对应的输出，将这个信号再输出出去即可。

其连接方法如下面图所示。

本质上是将输入的信号连接到使能控制端的低电平有效上，将选择的输出地址当作译码器正常的输入来看待。

这样就能实现将信号以设定好的位置输出出去。

相应的，如果将输入的信号连接到使能控制端的高电平有效上，其实现的结果就是将信号以取反的方法输出出去。

二 - 十进制译码器

这个的作用是将输入的 10 组 4 位二-十进制代码翻译成 $0\sim 9$ 十个对应信号输出的逻辑电路

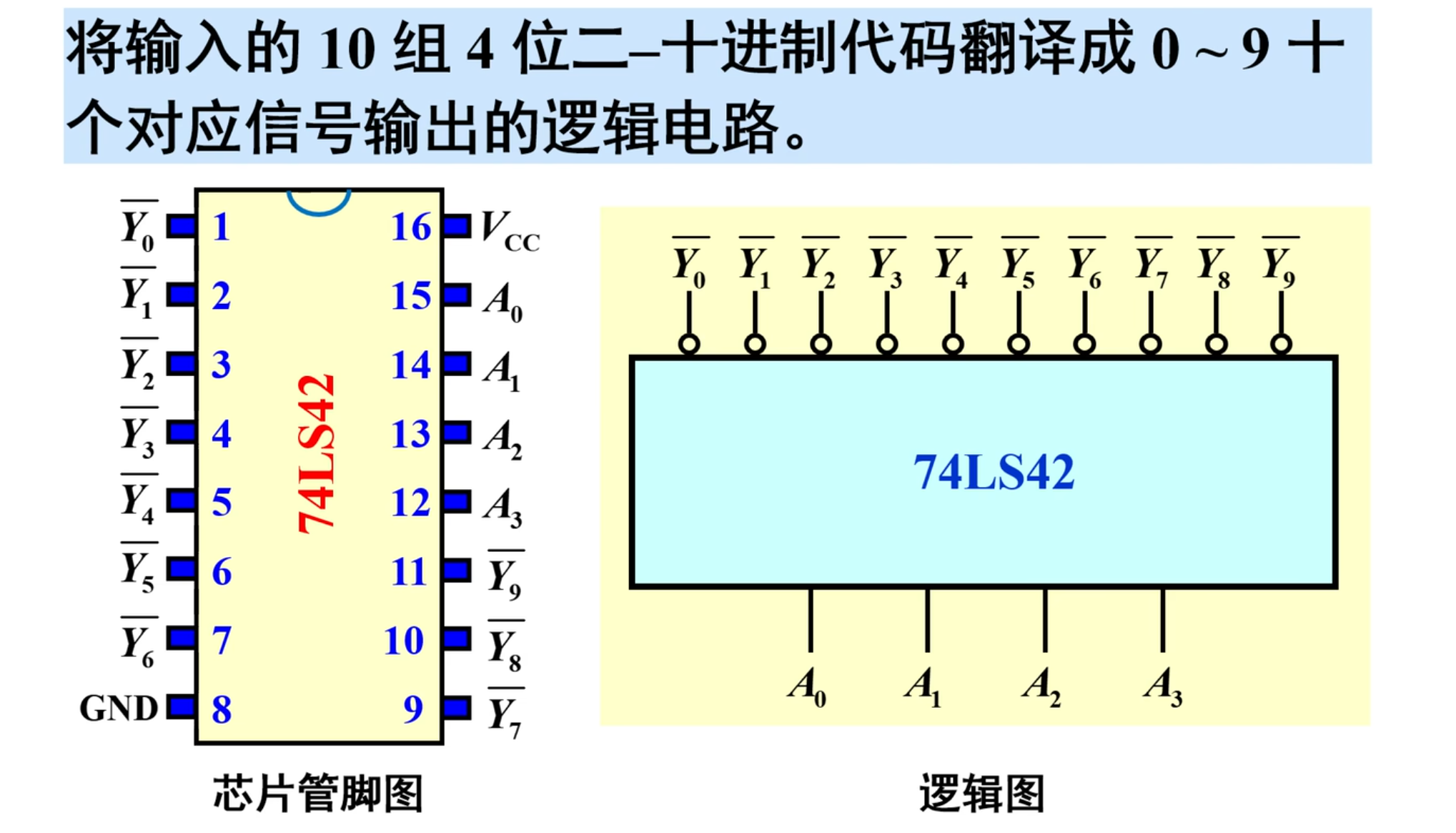
这个芯片是没有控制端的

有十个译码输出端，低电平 0 有效。还有四个 8421 BCD 码输入端，从高位到低位依次是 $A_3$ 、 $A_2$ 、 $A_1$ 和 $A_0$

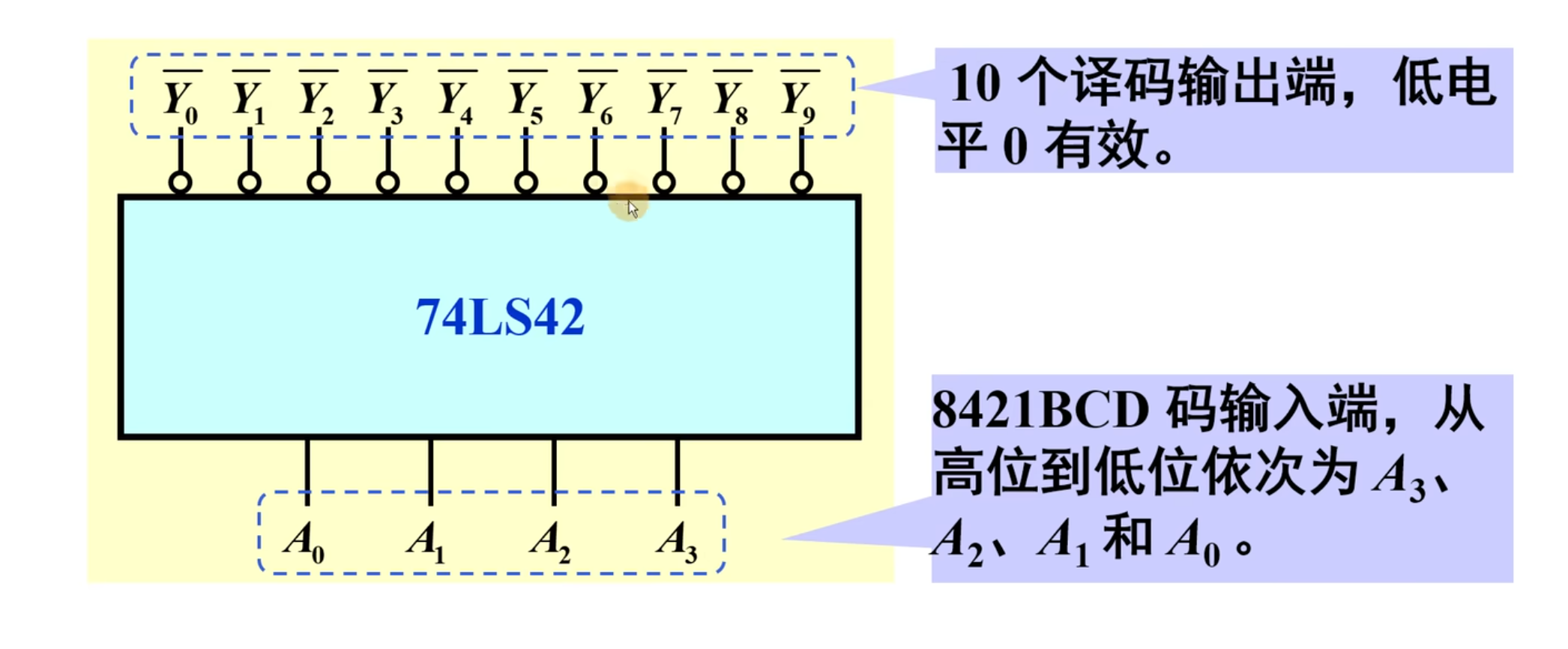
下面是它的功能表：

需要注意的是：虽然有四位输入，总共有 $2^4=16$ 种输入，但是有效的只有十种，这也就导致了有六种伪码。这六种伪码就全是无效电平。也就是 $1$

显示译码器

在之前学到的 138 也就是 3 线-8 线译码器，就是传统上的结果中只有输出是有效电平，剩下的都是无效电平（高电平 1）

但是在一些场合，不只是需要一个有效的信号输出，还需要多个有效的信号进行输出。

下面的显示译码器就是能多个有效信号的输出。

显示译码器：将输入的 BCD 码译成相应的输出信号，以驱动显示器显示出相应数字的电路

同样的，这个也是四个输出，十个输出，这也就意味着，在输入的时候，是有六个伪码的。这种编码称为不完全编码

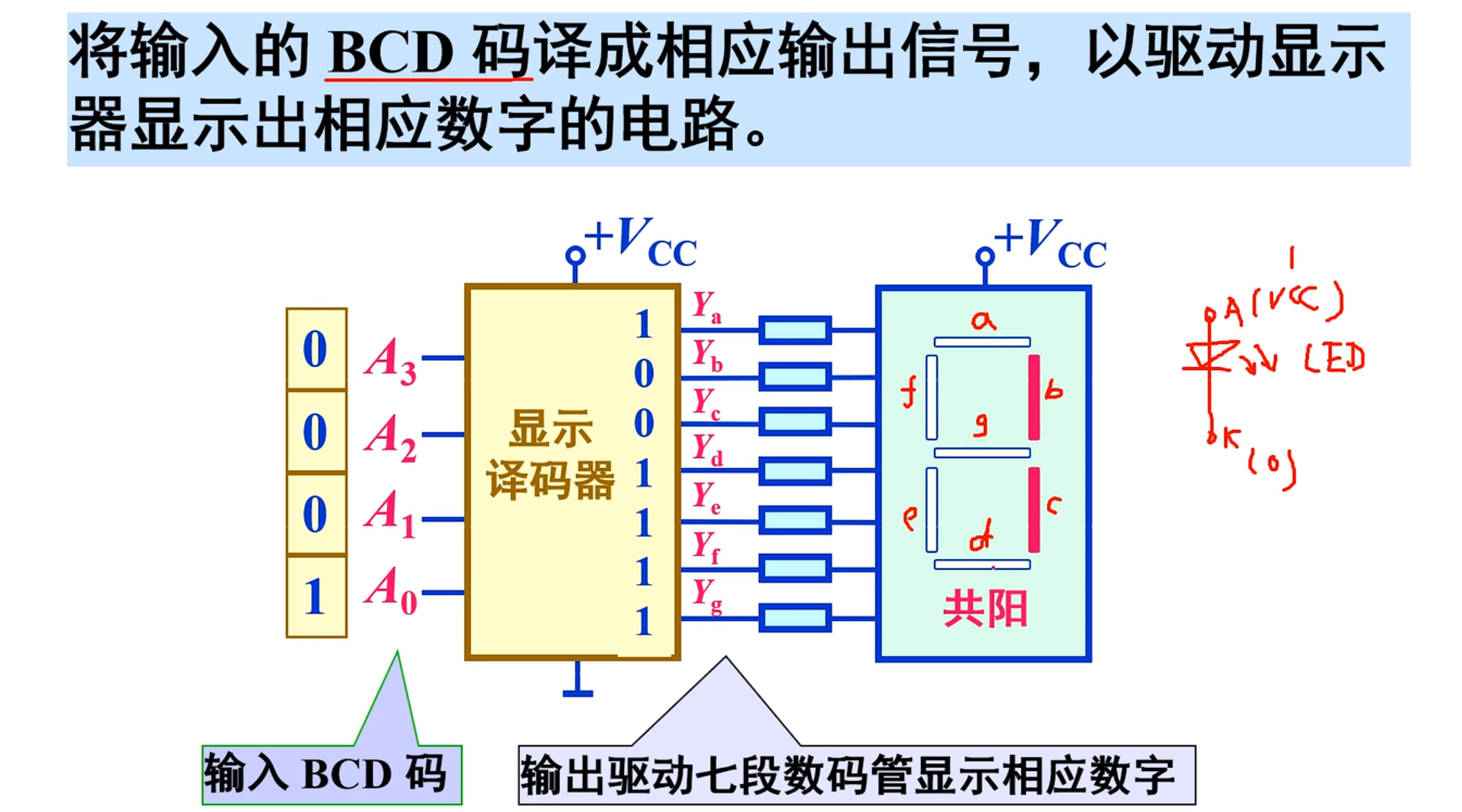
注意，在设计中，设计为 0 为亮，1 为不亮，本质上还是取反

在数字设备中用得比较多的是七段数码显示器，又称为是数码管。常用的有半导体数码显示器（LED）和液晶显示器（LCD）等，它们由七段可以发光的字段组合而成。

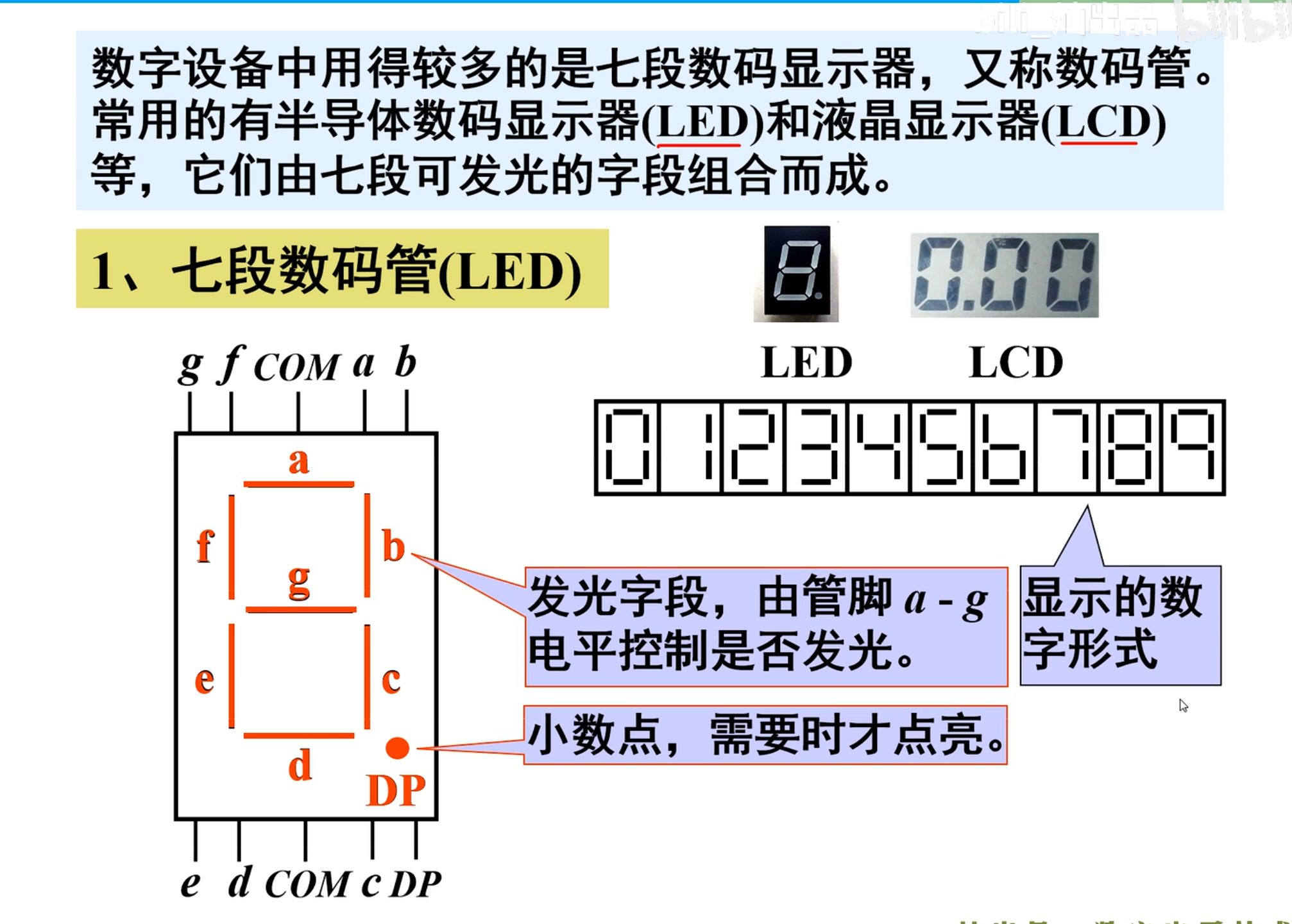
COM 端称为公共端，是将多个数码管串联到一起用的连接点。

NOTE

测试数码管是共阴极还是共阳极：可以用万用表来测试，如果黑表笔放到 COM 端，红表笔放到其中一个显示端（七个其中一个），亮了就是共阴极。红表笔放到 COM 端如果亮了就是共阳极

所以它有两种接法：

一个是共阳极接法，一个是共阴极接法

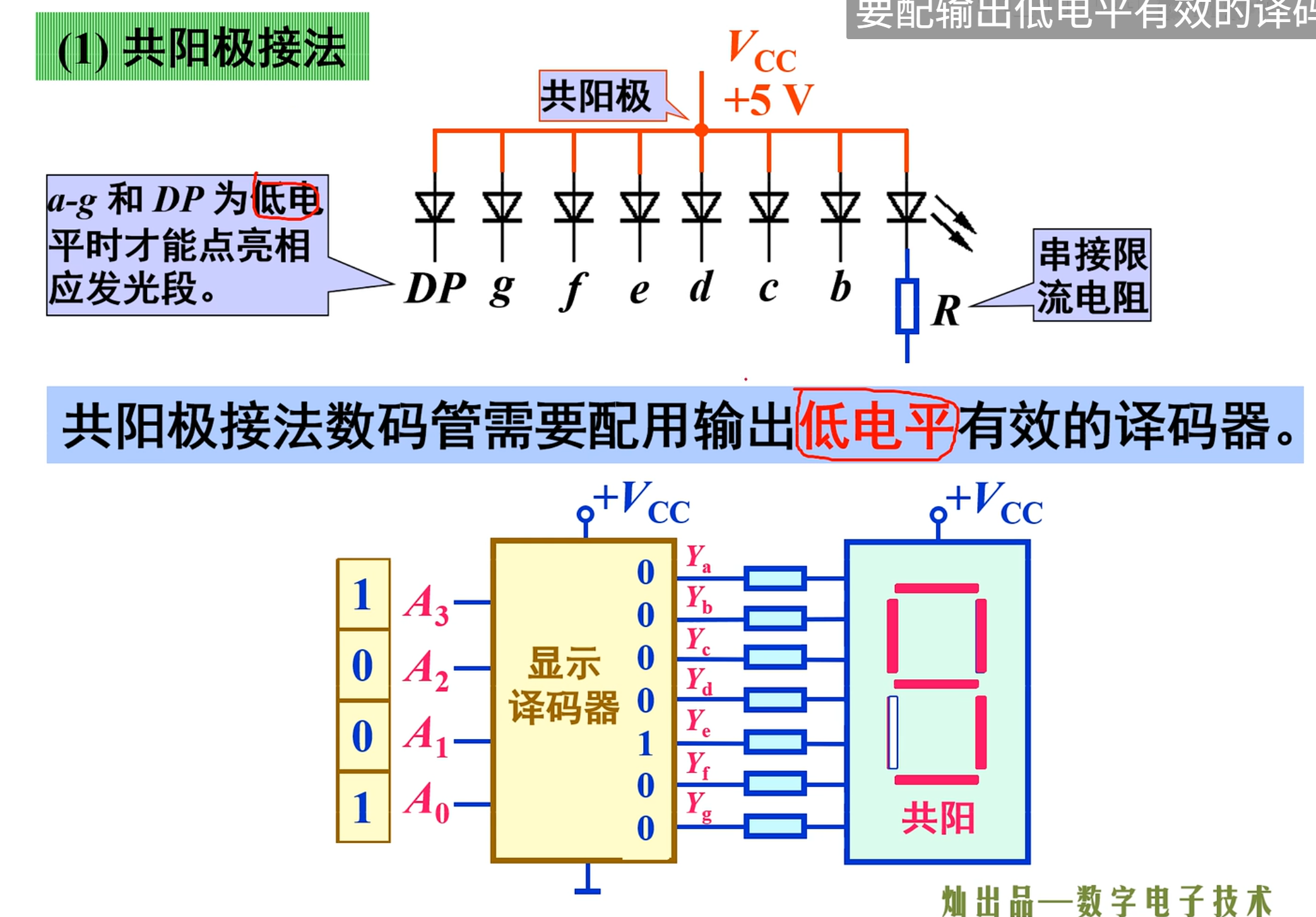
NOTE

共阳极接法的数码管需要配用输出低电平有效的译码器。

---

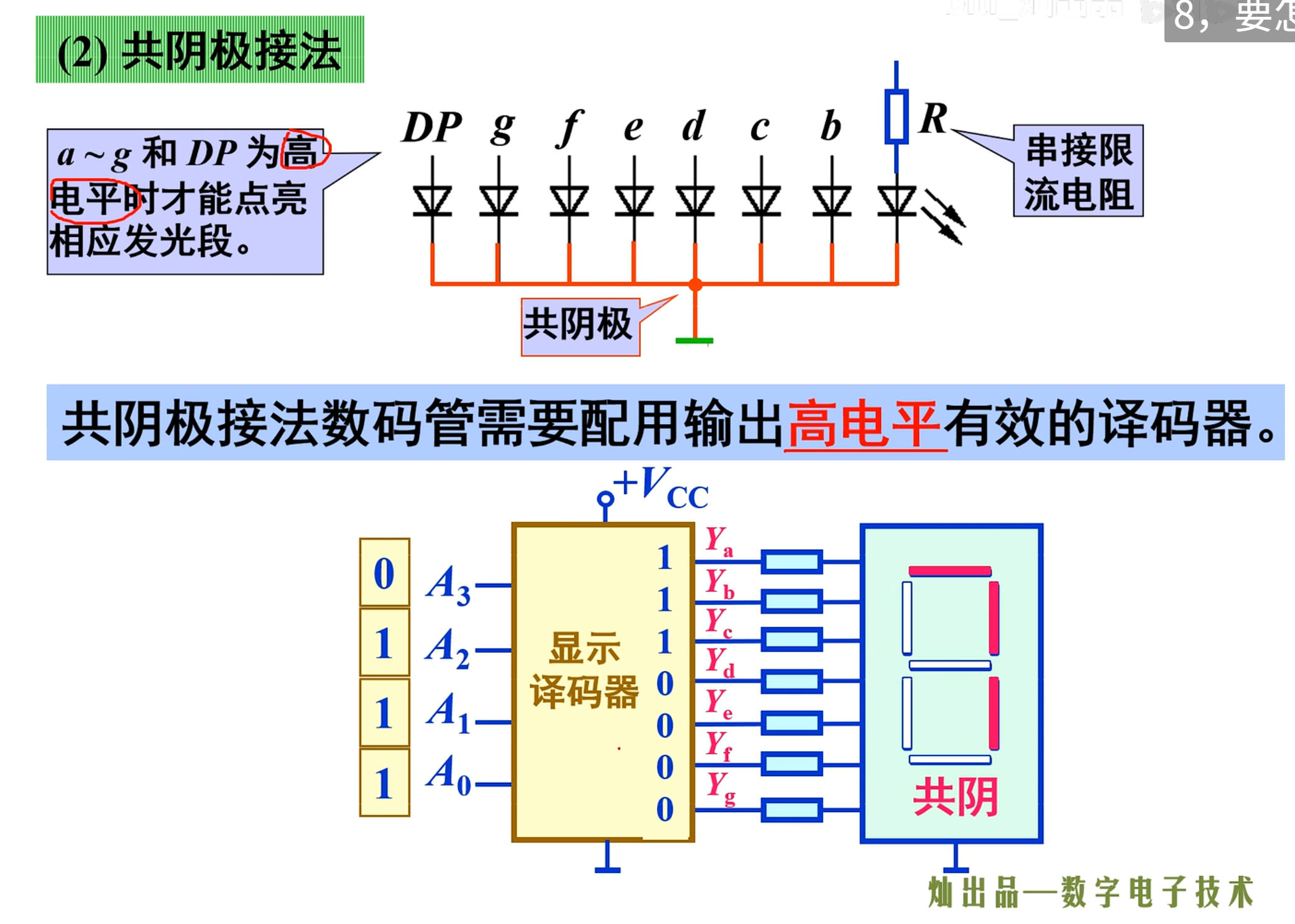
NOTE

共阴极接法的数码管需要配用输出高电平有效的译码器

---

补充：

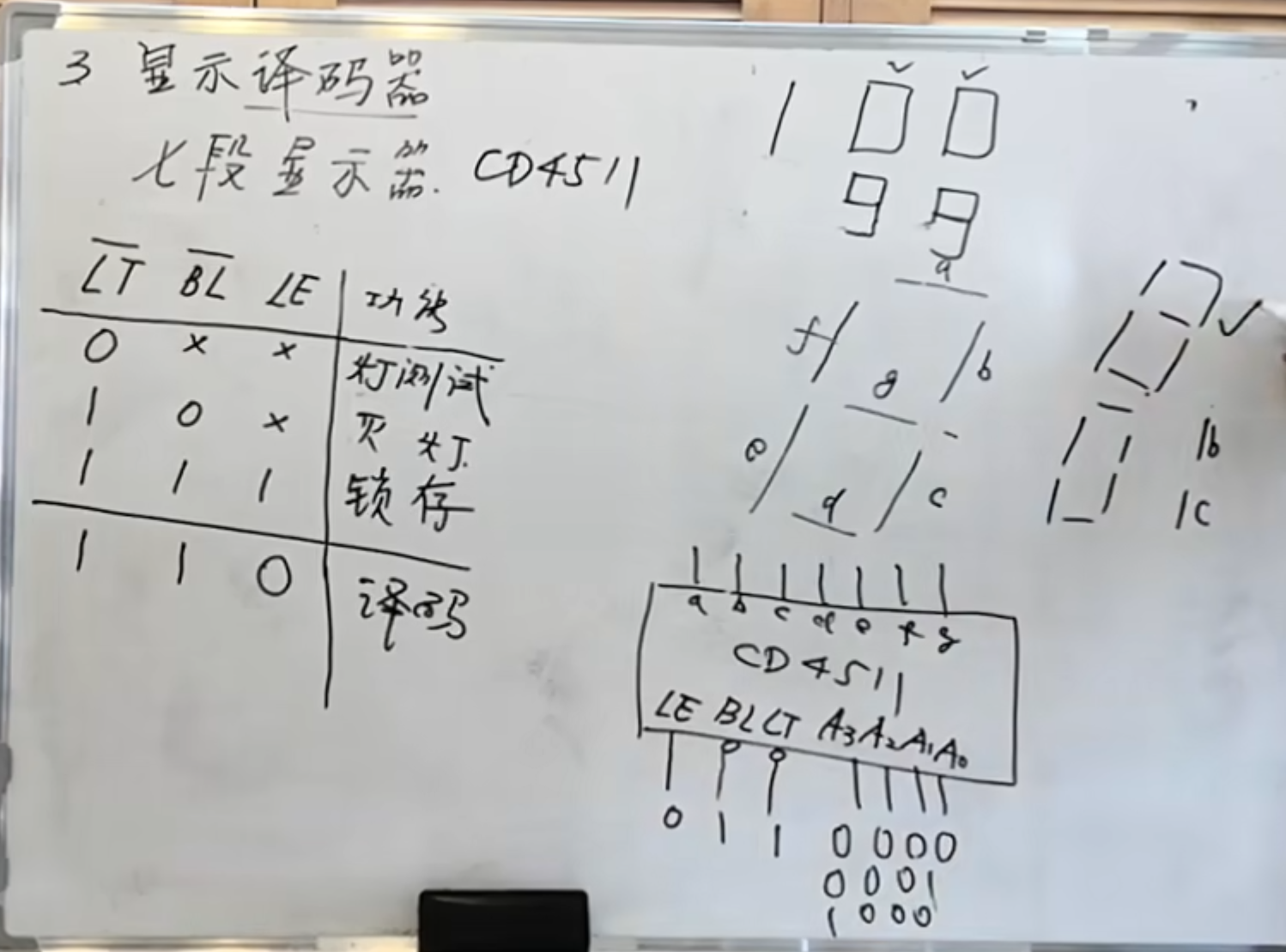
在显示译码器中，相比较于传统的译码器，虽然也有三个使能端，但是实现的功能还是不一样的。

这里的使能端更像是一种能够实现更多功能的控制器

具体控制方法如上面图中所示。

只有当 $\overline{LT}=1$ ， $\overline{BL}=1$ ， $LE=0$ 的时候才正常译码

下面是正常译码的时候逻辑表

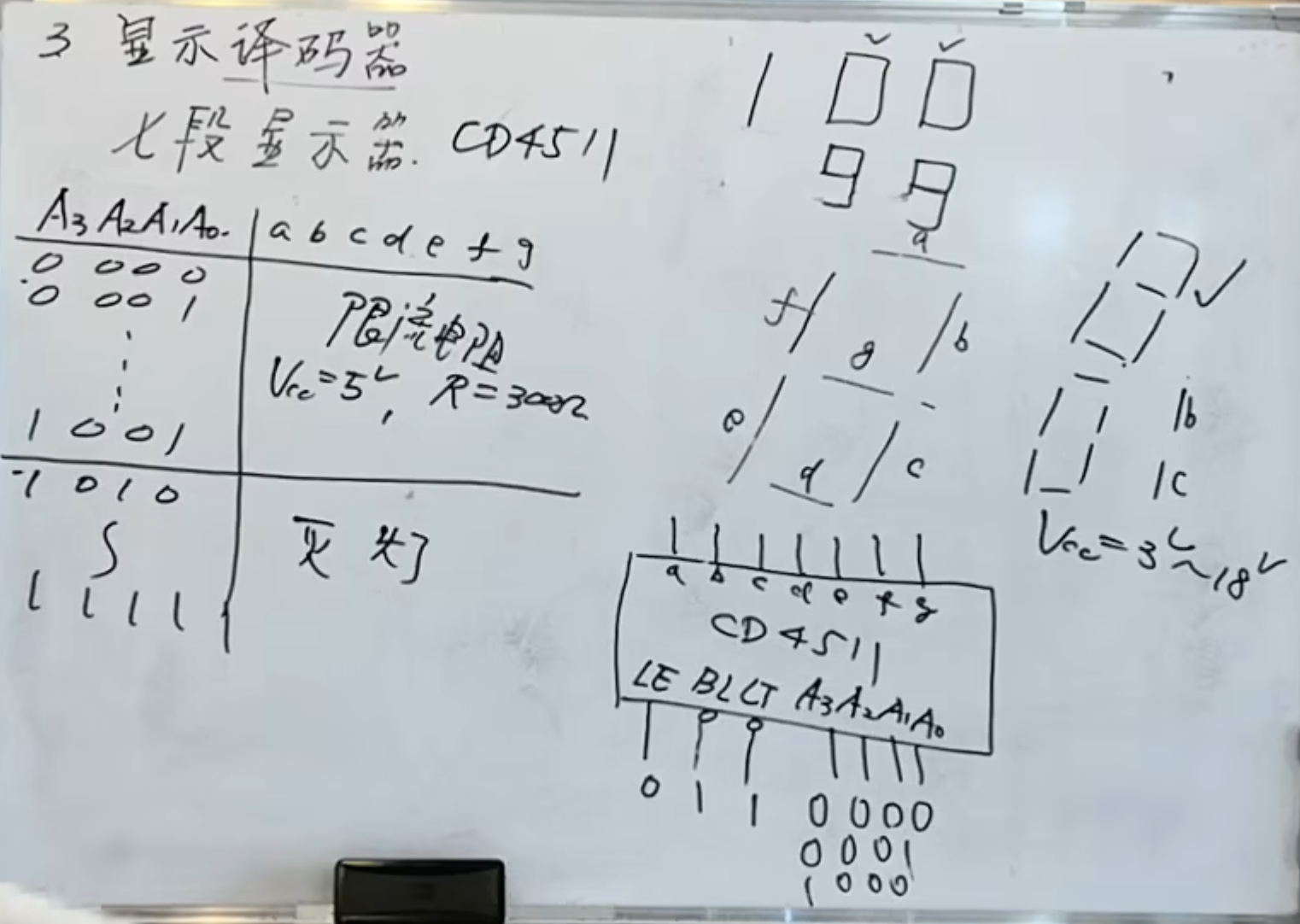
需要注意的是，当出现无效码的时候，显示译码器是灭灯的

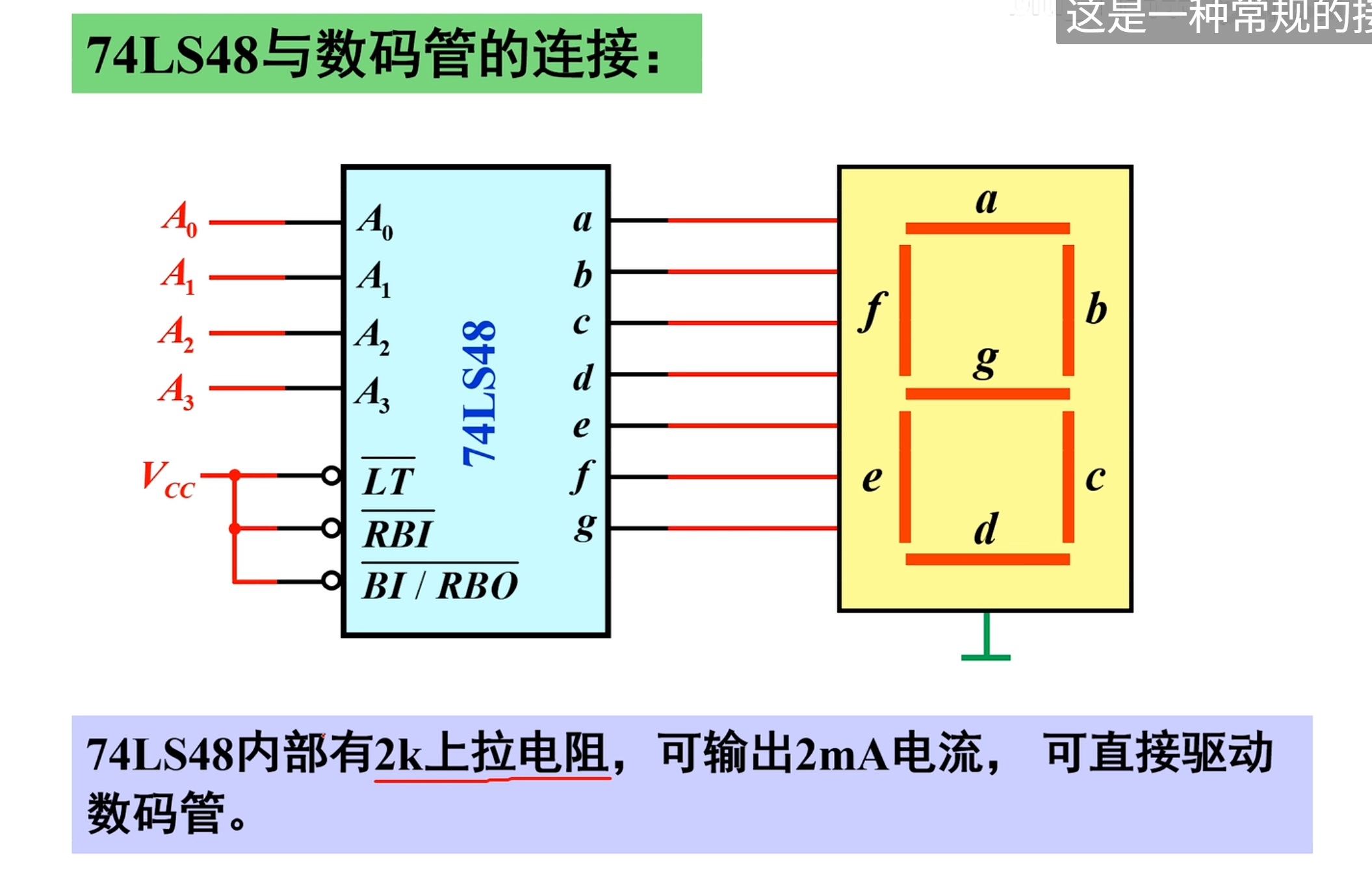
48 集成译码器（显示）

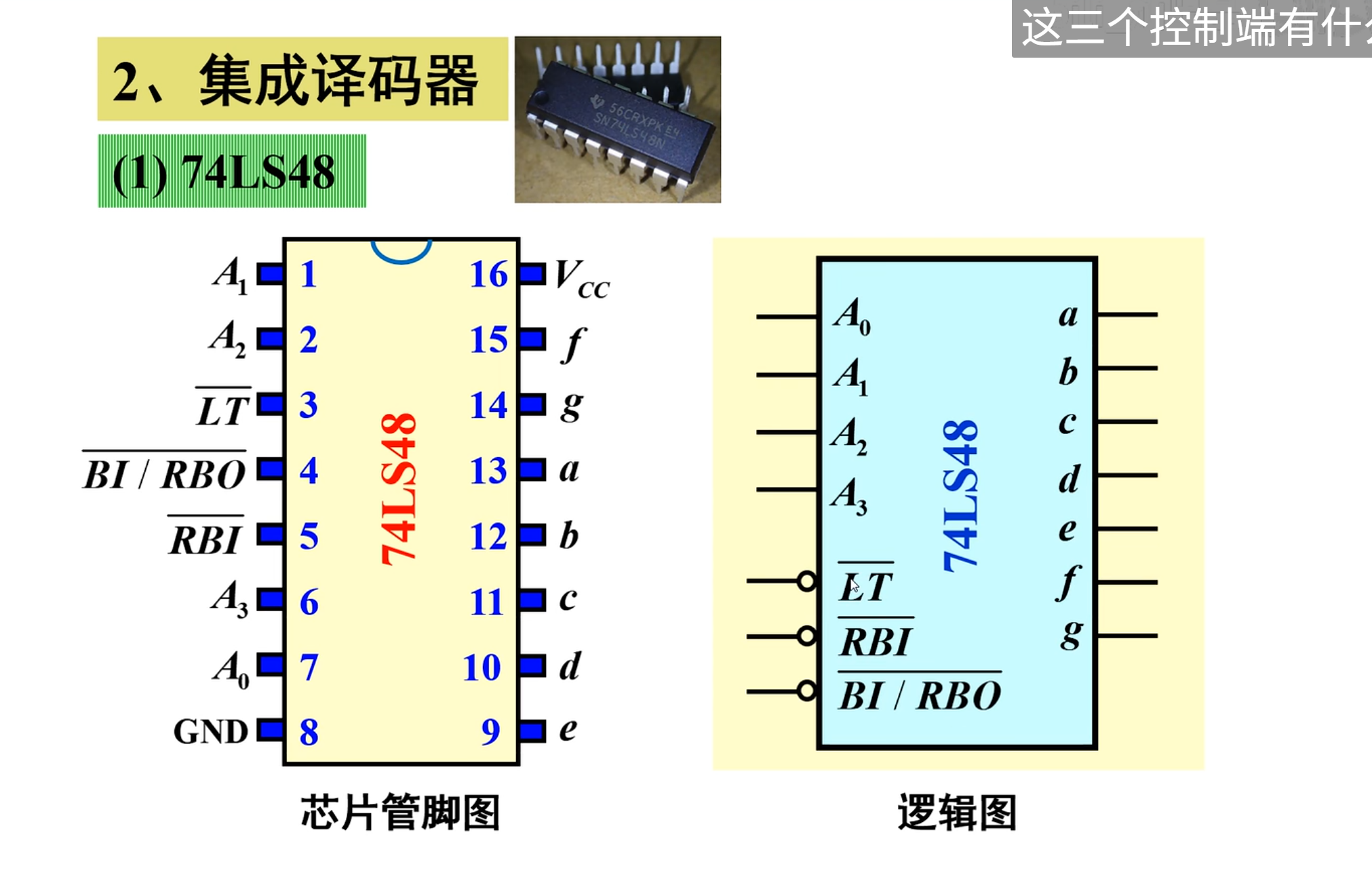
48 的输出端高电平有效，需要与共阴极数码管配合才行

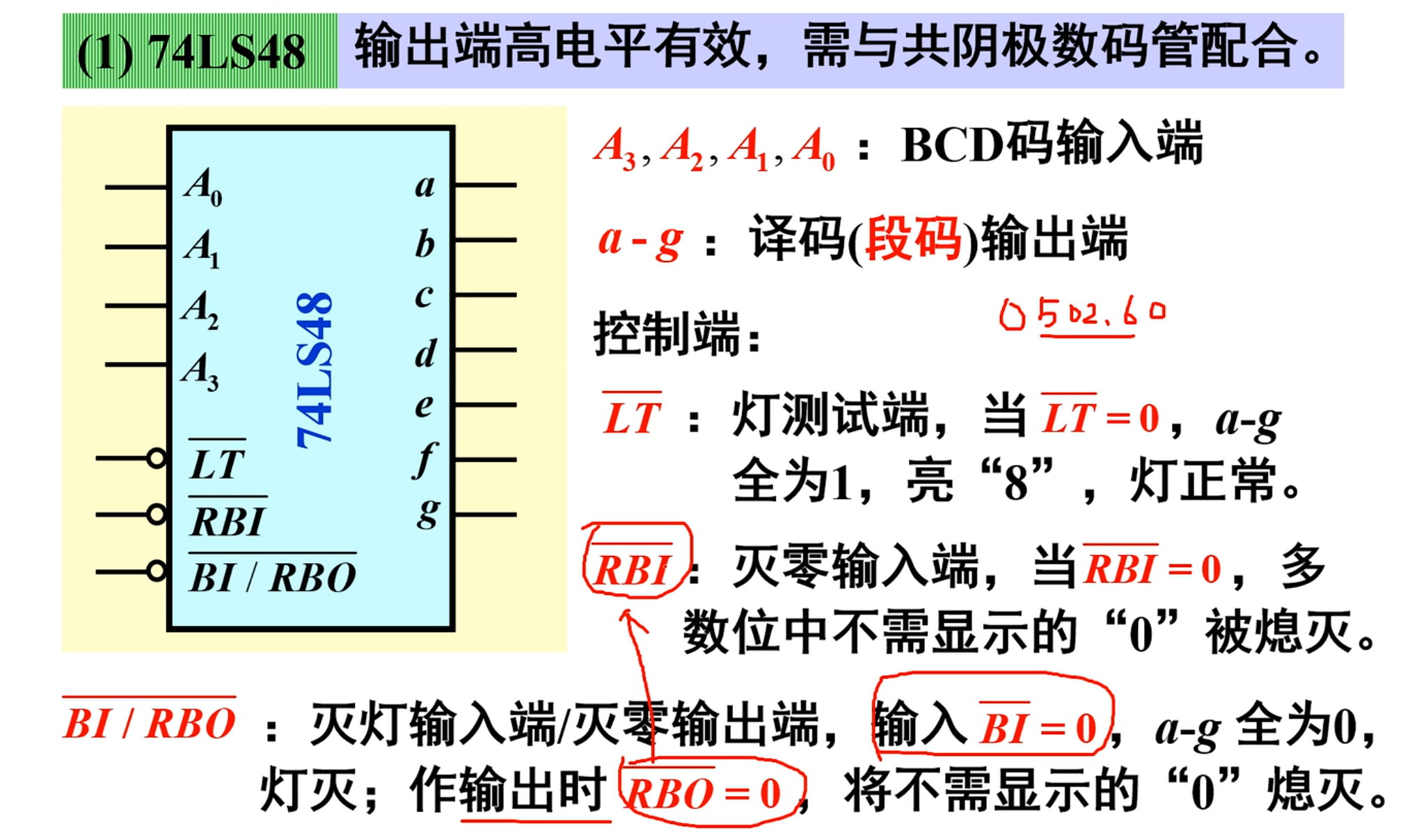
这里需要注意的是最后一个控制端：（ $\overline{BI/RBO}$ ），这个是既可以当作输入，也可以当作输出。

本质上在后面的功能表上有说明，当其他的输入都无效的时候，这个时候的 $\overline{BI/RBO}$ 是当作输入来用的，输入为 $0$

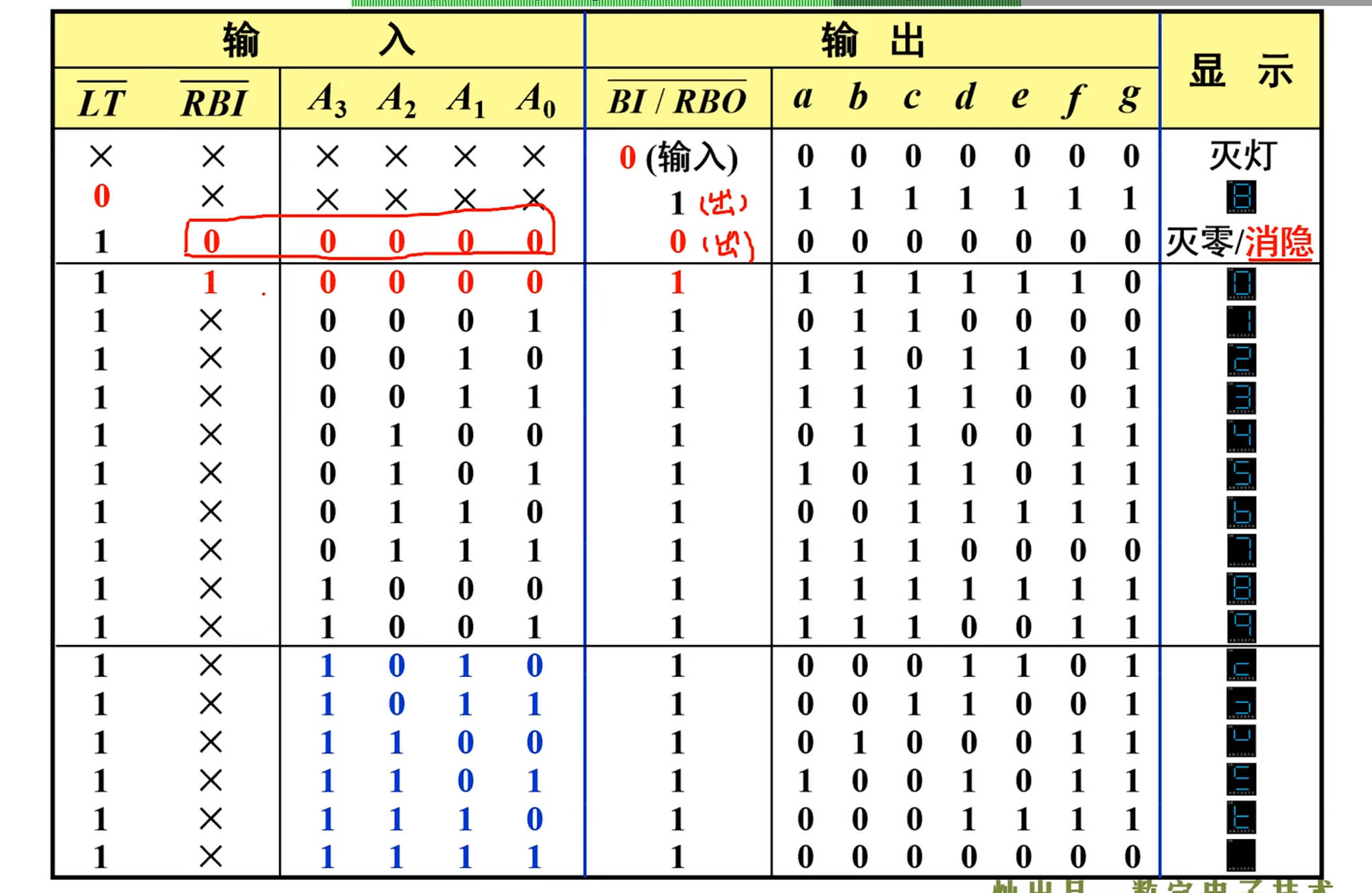
此外，当 $\overline{RBI}$ 和 $A_3$ 、 $A_2$ 、 $A_1$ 、 $A_0$ 输入都为 0 的时候，才控制为消隐（灭零）

下面这种接法是一种常规接法：

下面是多位的显示译码器连接到一起实现多位数码管的动态灭零连接电路

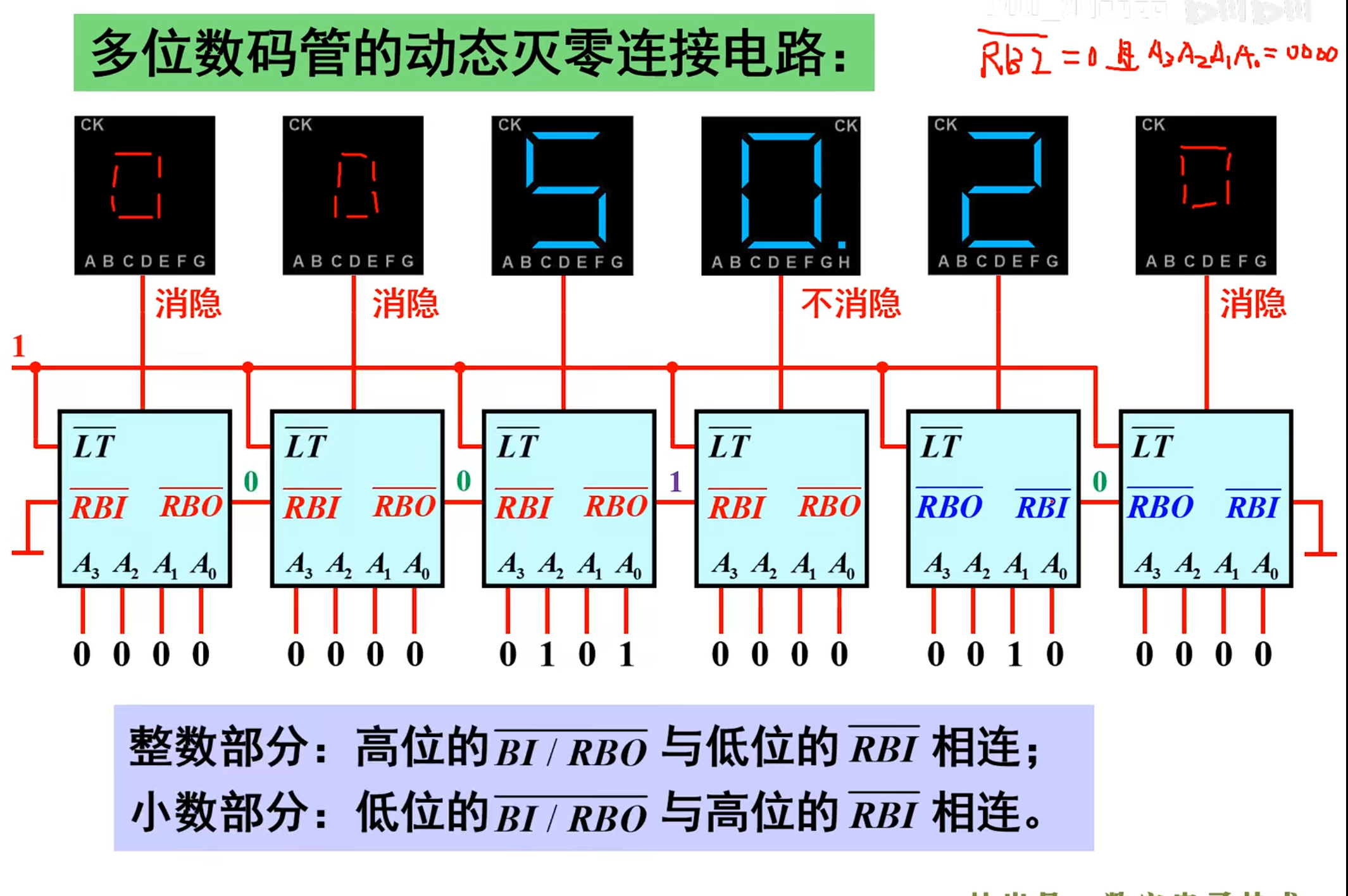
其中，整数部分：高位的 $\overline{BI/RBO}$ 和低位的 $\overline{RBI}$ 相连

小数部分：低位的 $\overline{BI/RBO}$ 与高位的 $\overline{RBI}$ 相连

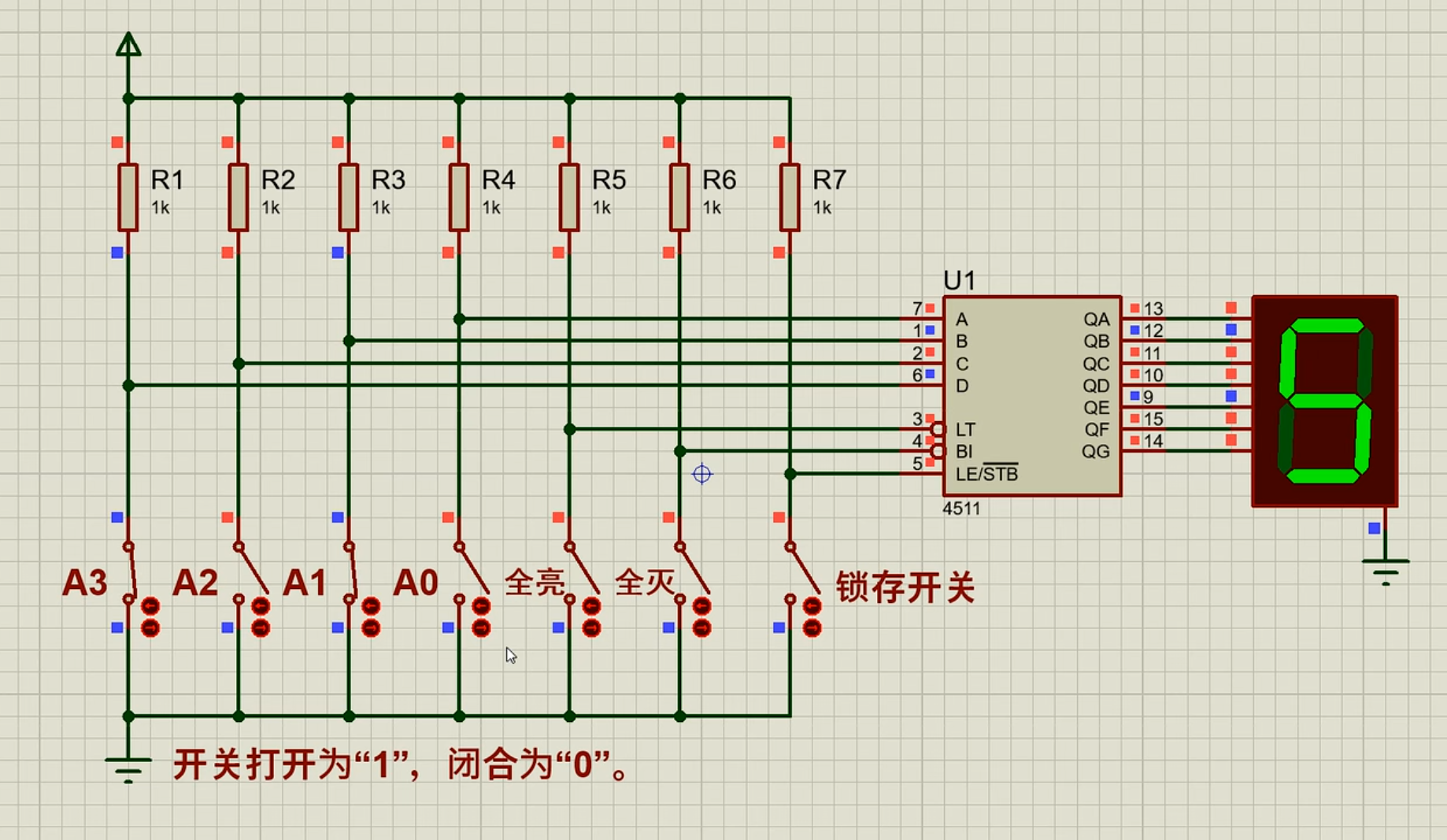
COMS 4511 集成译码器

其输出端高电平有效，需要与共阴极数码管配合

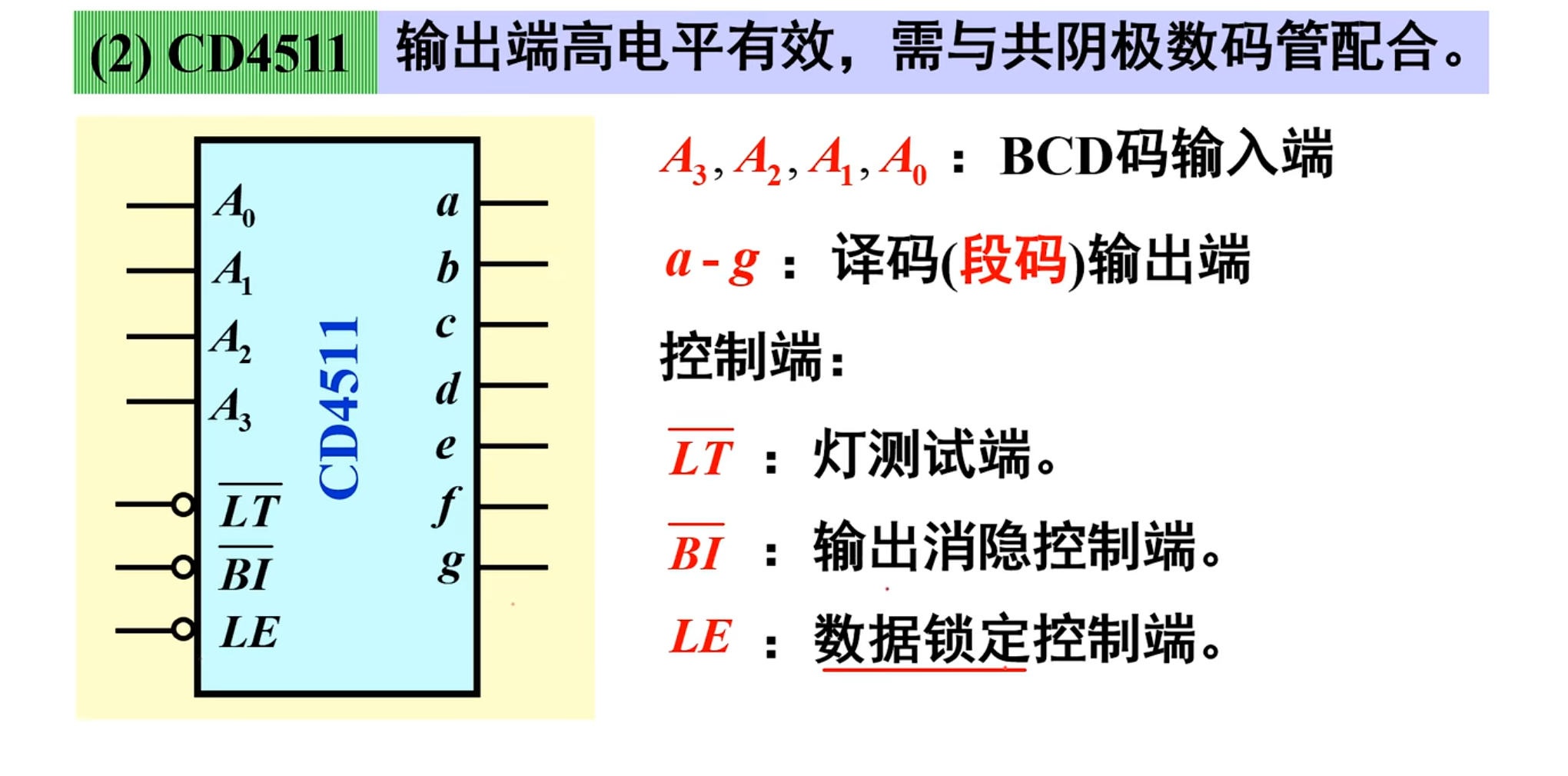
下面是逻辑图：

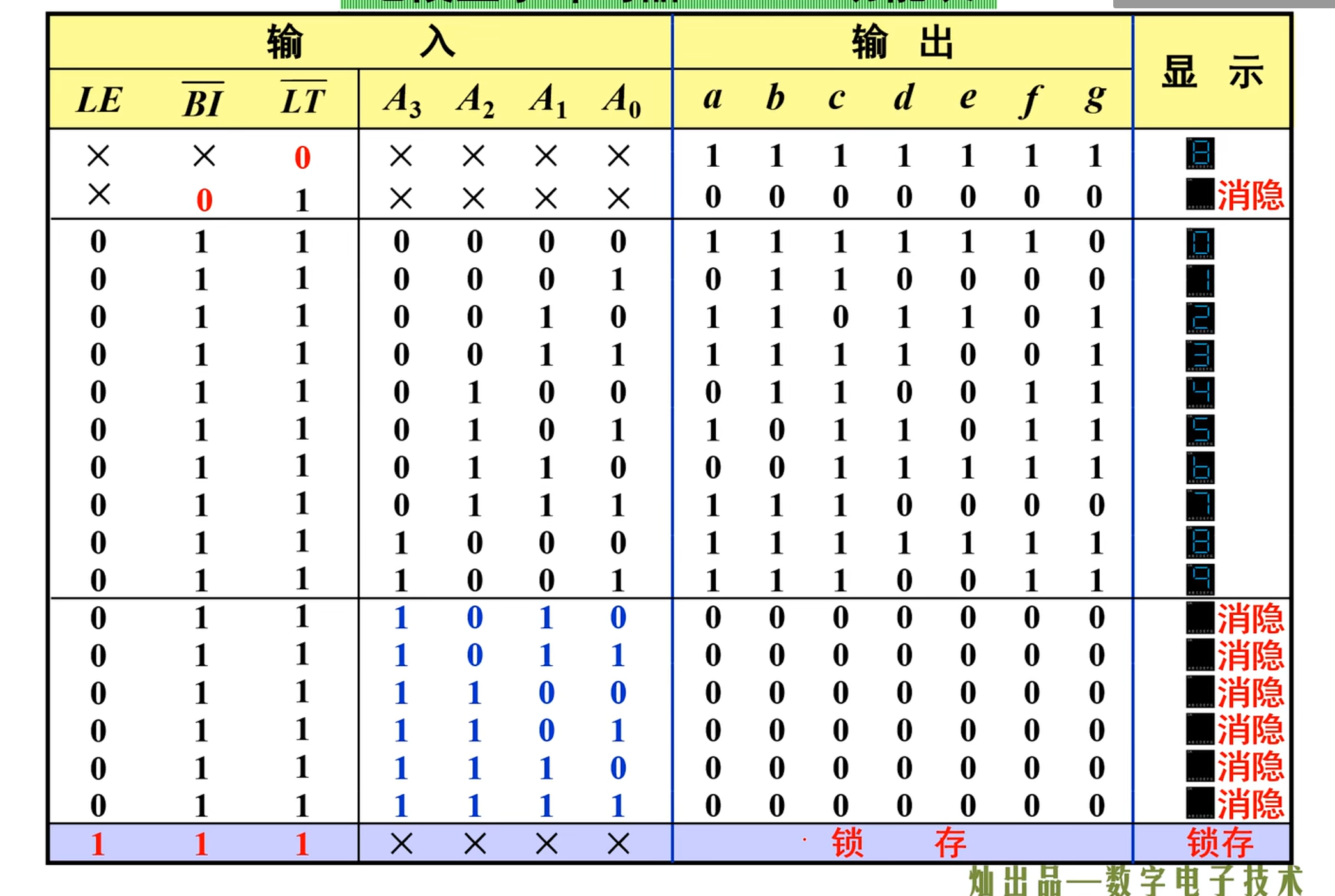
相对于原来的 48 译码器，其在无效码的时候也是消隐的。

并且在控制端都为高电平的时候，能够将上一次的输入进行锁存

在锁存之后，无论再输入什么都是被锁住的哪个数

数据选择器

数据选择器：根据地址信号的要求，从多路输入数据中选择其中一路输出的逻辑电路。又称为多路选择器（Multiplexer，简称为 MUX）或者多路开关

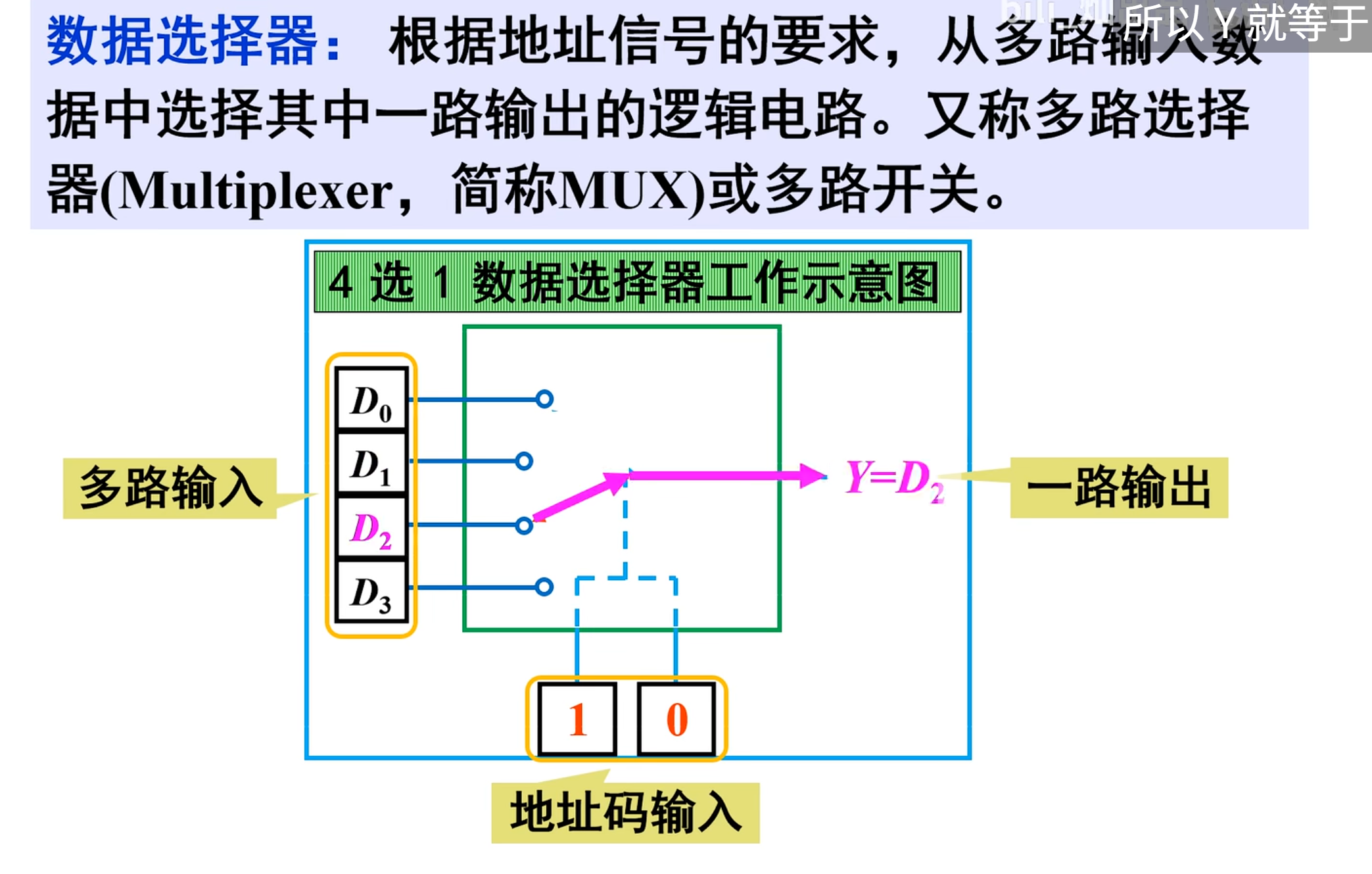
数据选择器的输入信号个数 $N$ 与地址码个数 $n$ 的关系为 $N=2n$

常用 2 选 1、4 选 1、8 选 1 和 16 选 1 等数据选择器。

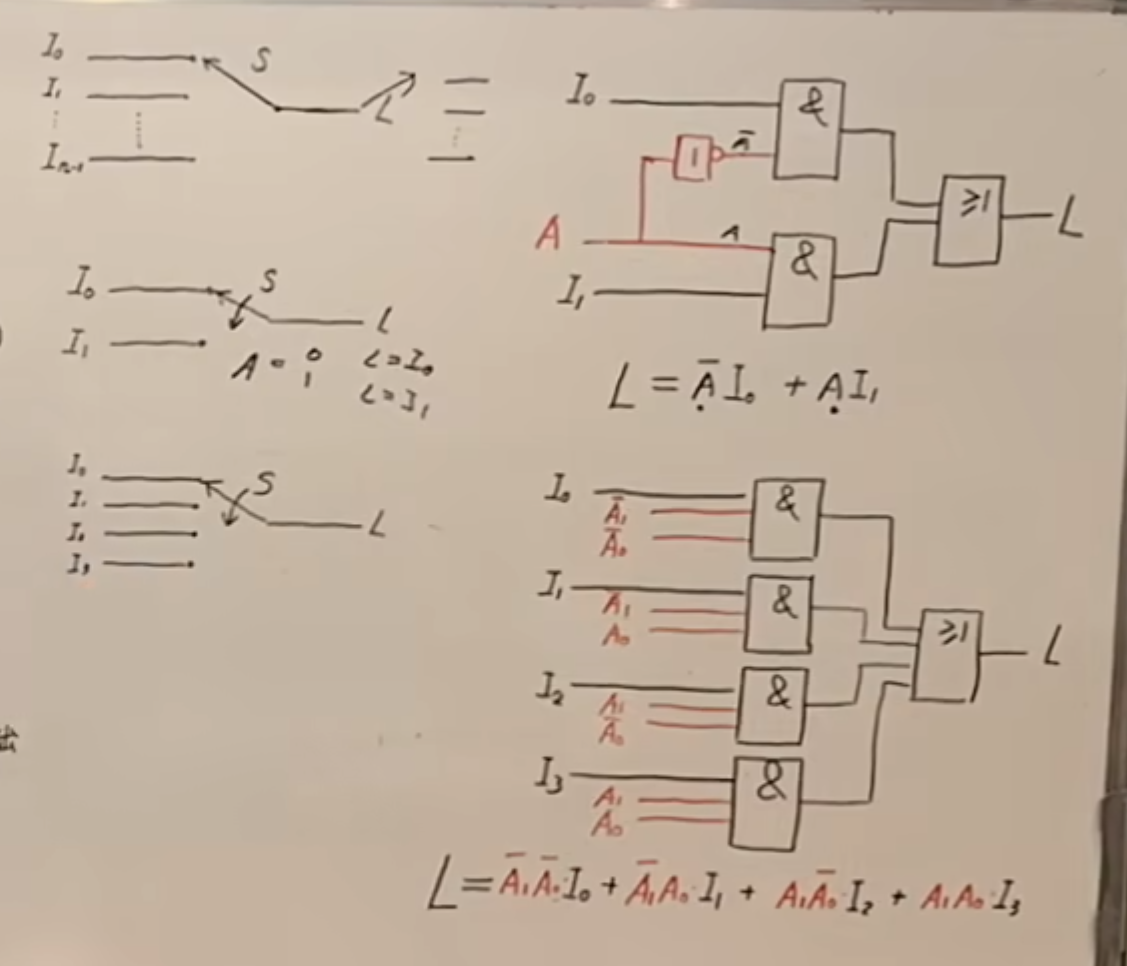
其中二选一以及四选一的类似电路图如上面图中所示。

最常见的方法就是使用与或式

4 选 1 数据选择器（153）

下面以做题的形式来实现数据选择器

题意可知，数据选择器有 $4$ 个数据输入端， $1$ 个输出端。数据输入端分别用 $(D_0)$ 、 $(D_1)$ 、 $(D_2)$ 、 $(D_3)$ 表示，有数据输入时，用 $1$ 表示，任意值用 $(\times )$ 表示。地址输入端用 $(A_0)$ 和 $(A_1)$ 表示。使能控制端用 $(\overline{ST})$ 表示。

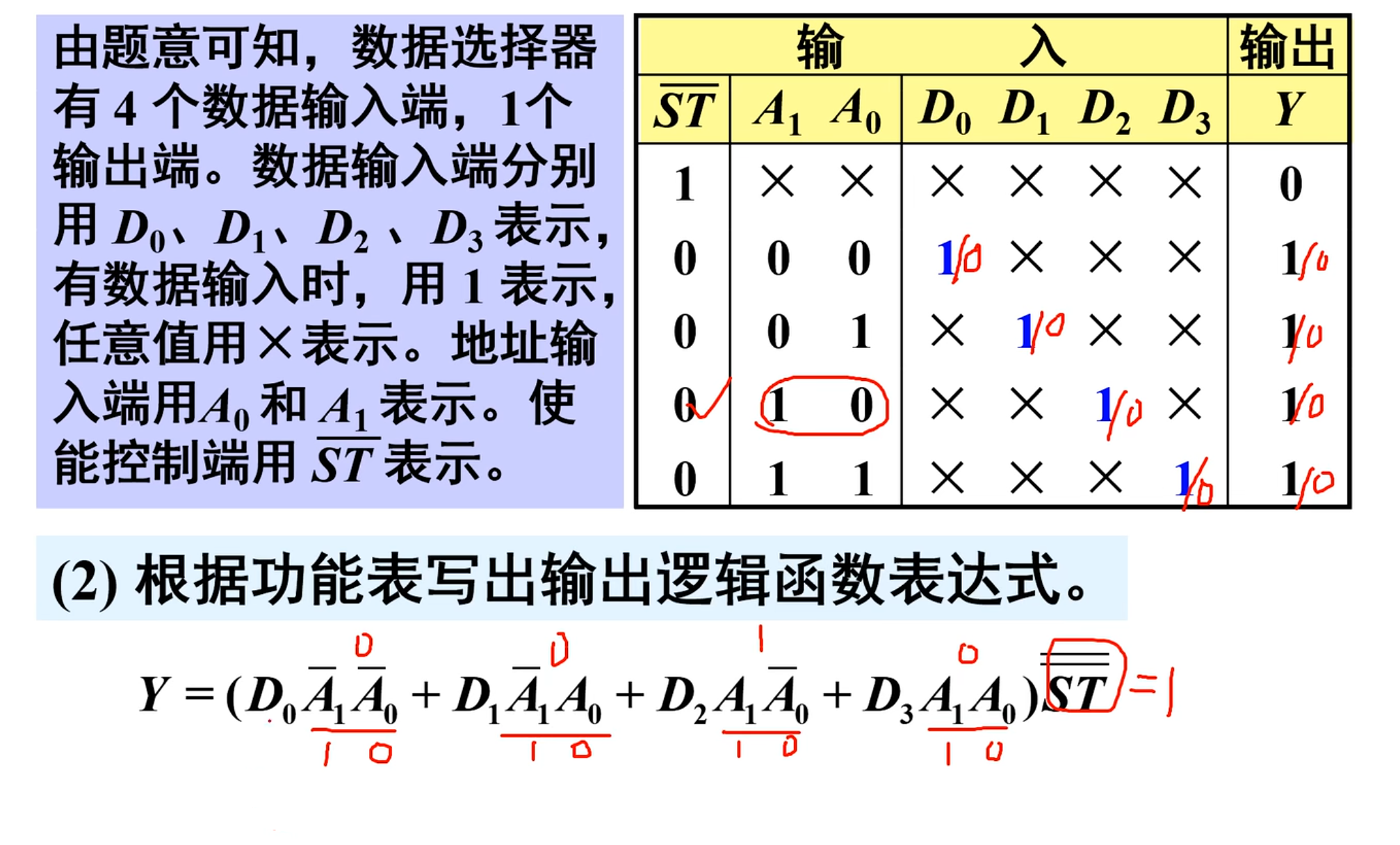
逻辑表达式为：

$$\begin{array}{r}Y=(D_0\overline{A_1}\cdot \overline{A_0}+D_1\overline{A_1}{A}_0+D_2{A}_1\overline{A_0}+D_3{A}_1{A}_0)\overline{\stackrel{―}{ST}}\end{array}$$

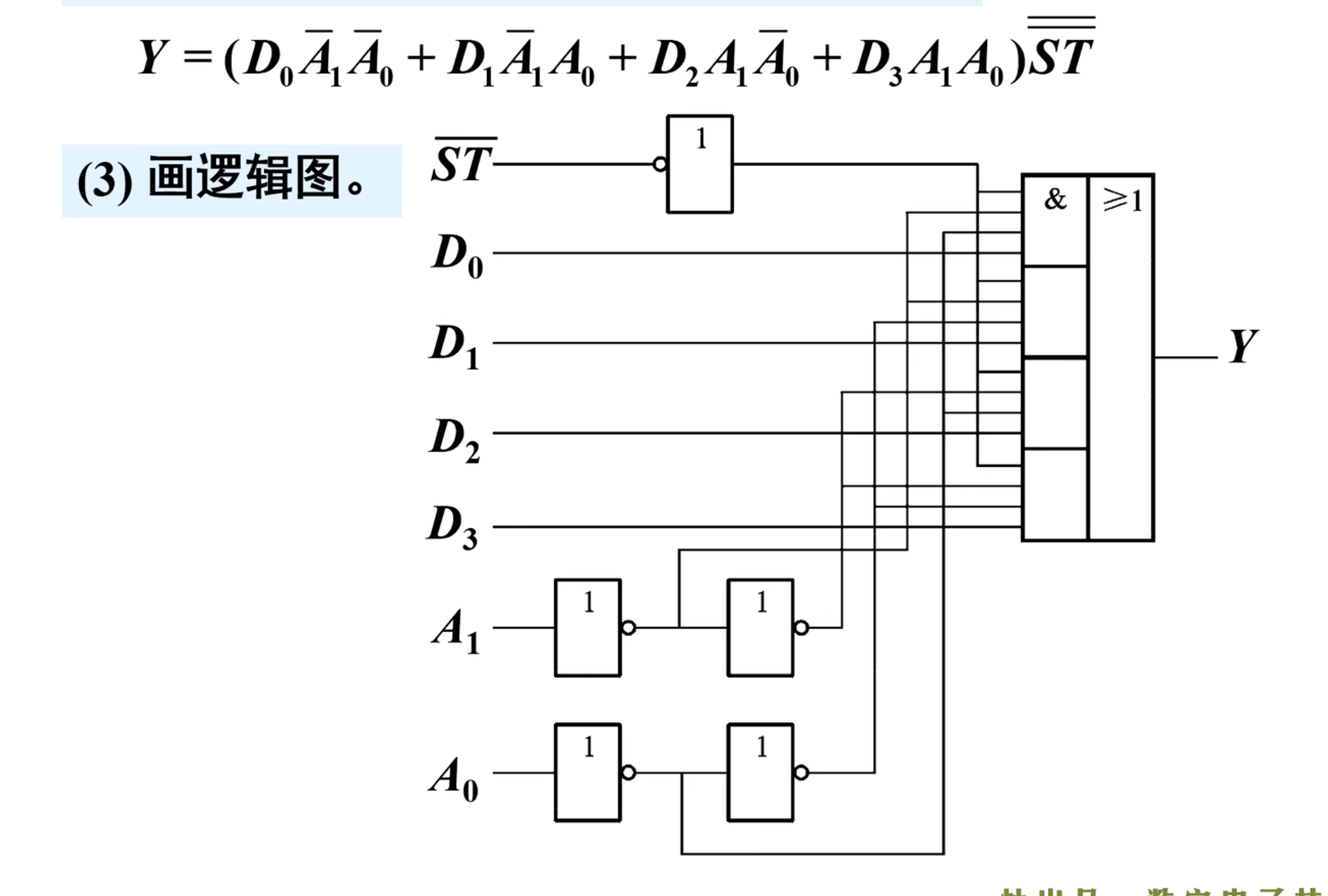
然后是画出电路逻辑图

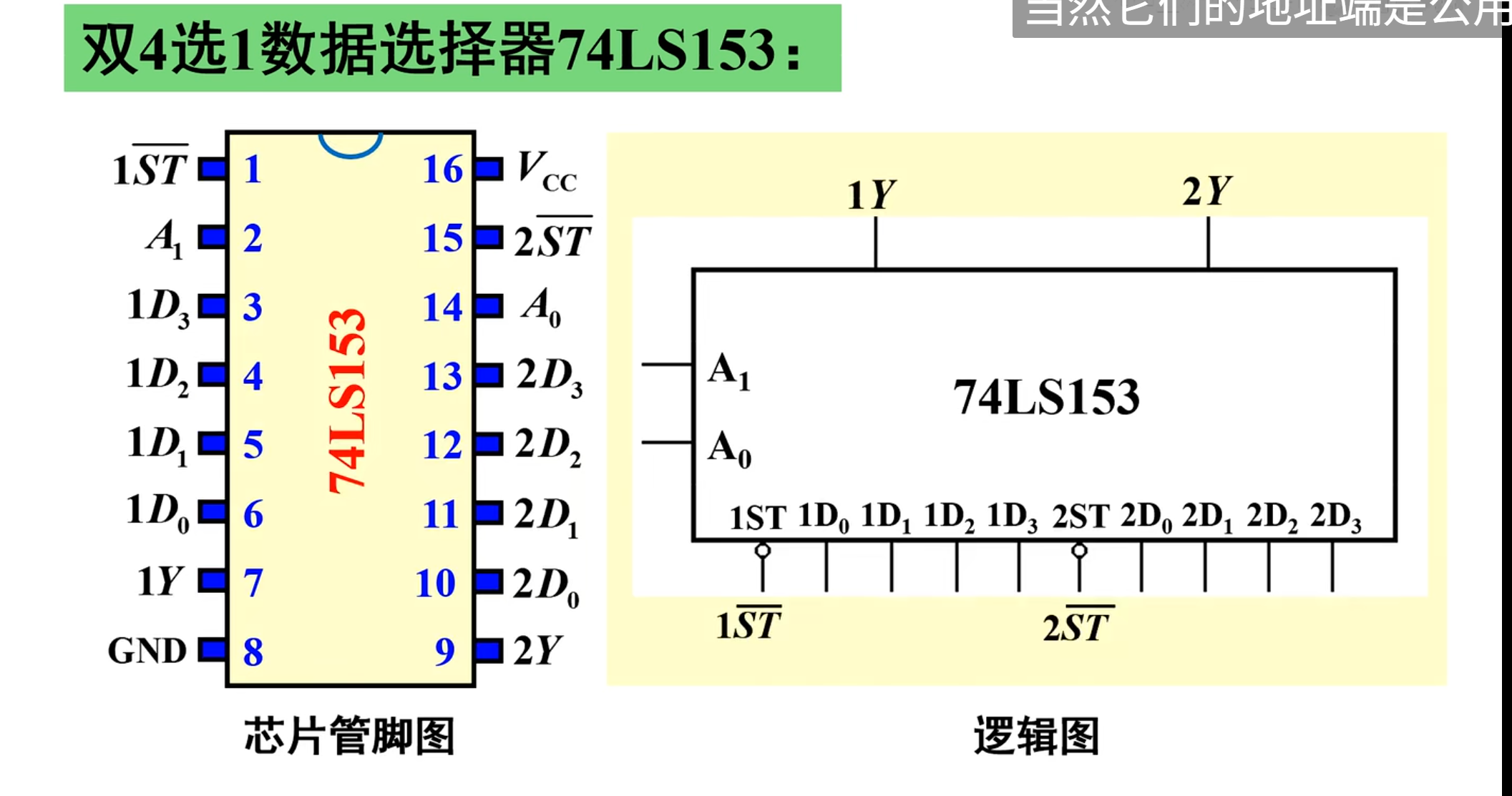
下面的集成电路为：

74 LS 153，当然这个数据选择器是一个双路的，也就是上面有两个 4 选 1 数据选择器，而他们的地址段是通用的

功能表如下：

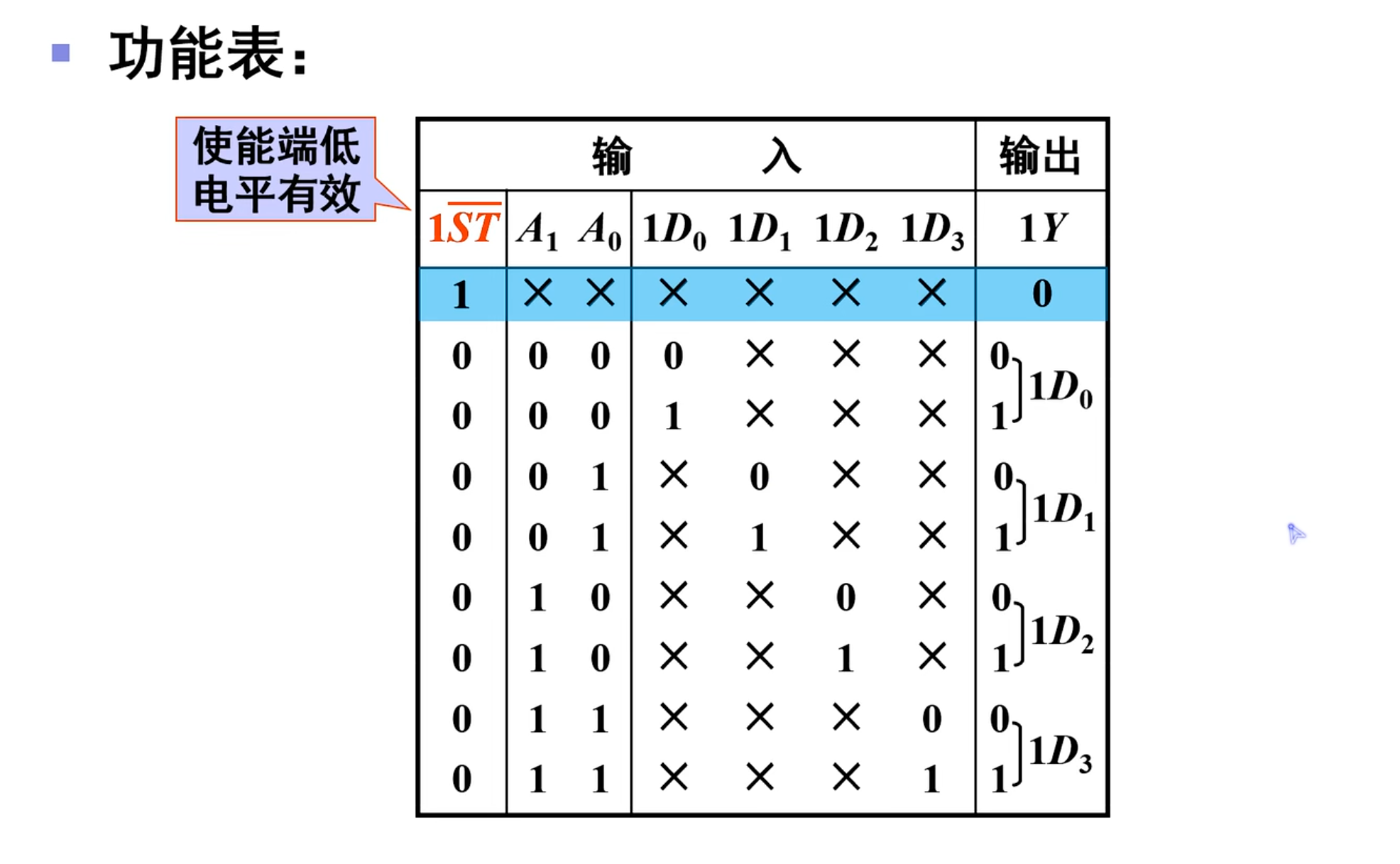
在这个地方可以看出来数据选择器又称为是最小项输出器

NOTE

令数据 $D_0\sim D_3$ 有些为 $0$ ，有些为 $1$ ，或者为其他变量，可以构造不同的逻辑函数

8 选 1 数据选择器（151）

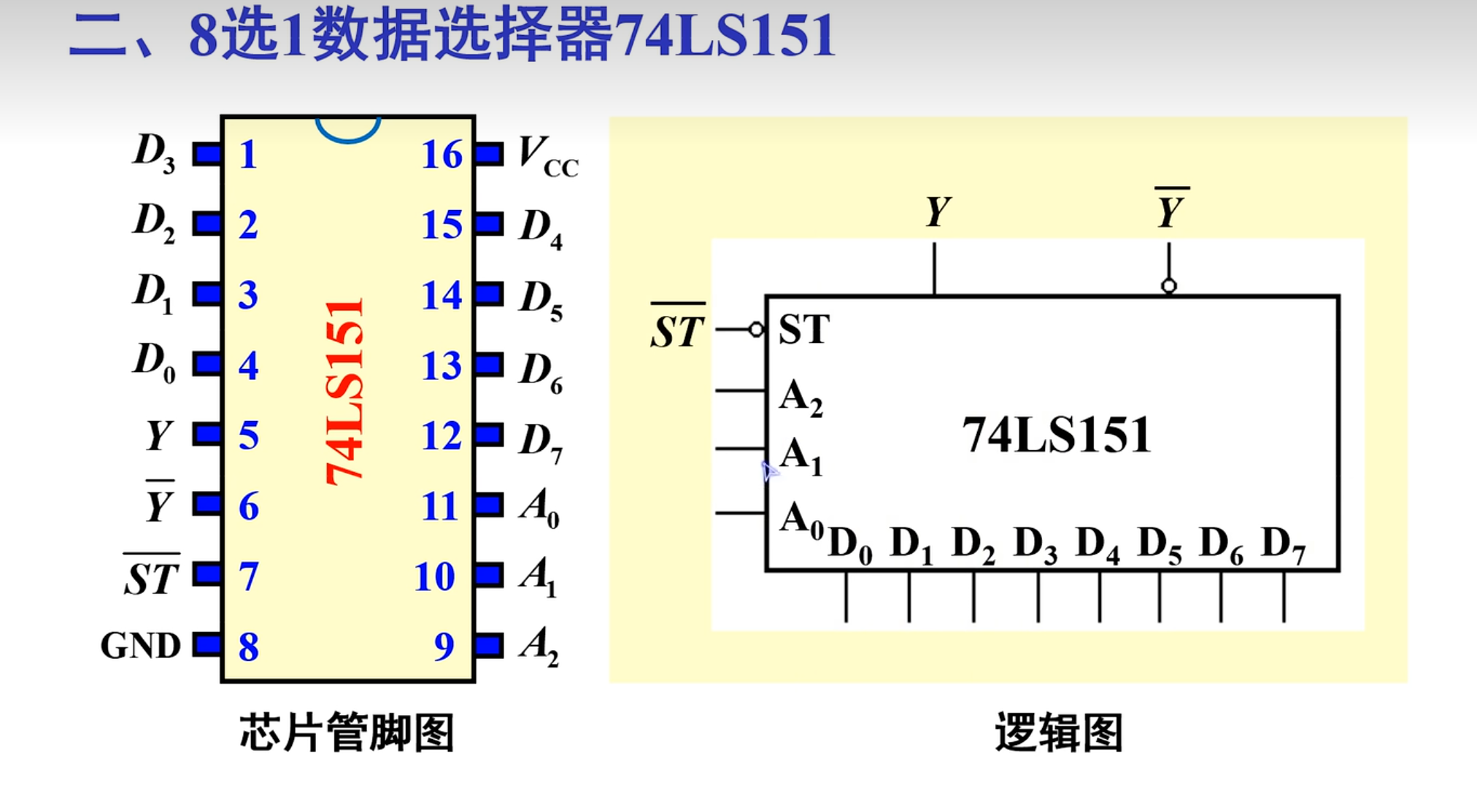
下面是功能表：

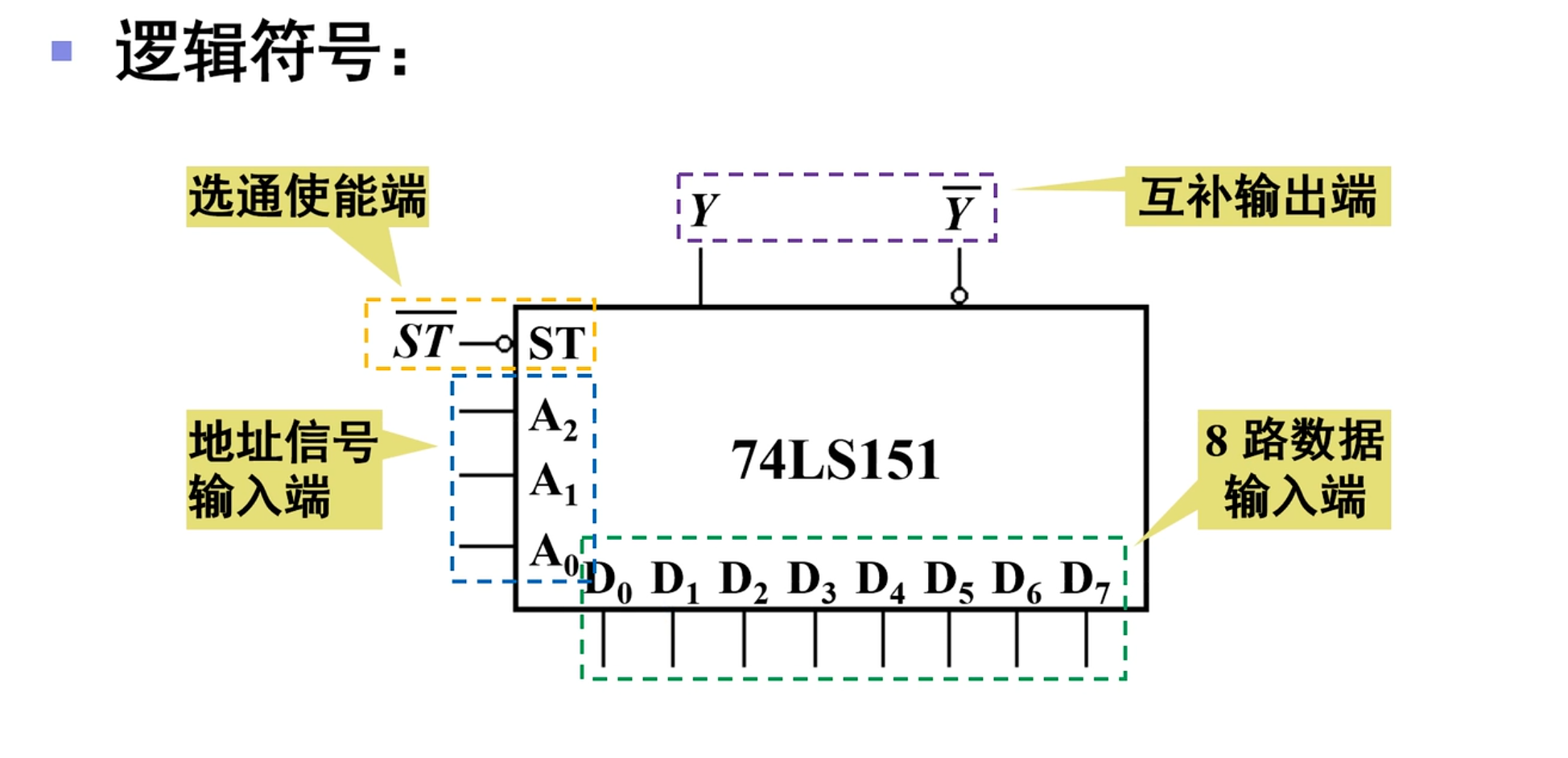
然后是真值表：

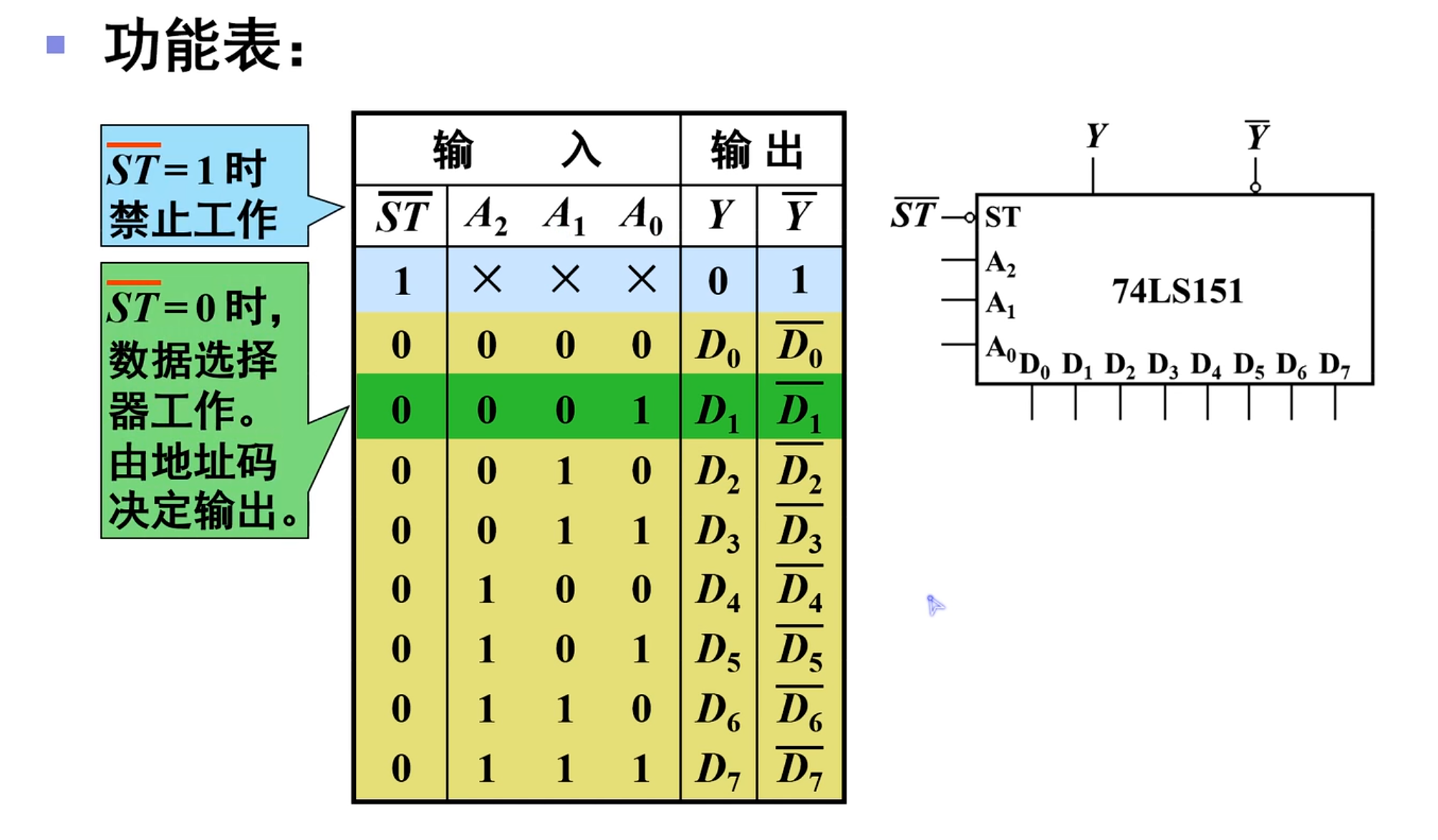
下面是输出表达式：

$$\begin{array}{rl}Y& =D_0\overline{A_2}\overline{A_1}\overline{A_0}+D_1\overline{A_2}\overline{A_1}{A}_0\\ & +D_2\overline{A_2}{A}_1\overline{A_0}+D_3\overline{A_2}{A}_1{A}_0+D_4{A}_2\overline{A_1}\overline{A_0}+D_5{A}_2\overline{A_1}{A}_0\\ & +D_6{A}_2{A}_1\overline{A_0}+D_7{A}_2{A}_1{A}_0\\ & =D_0{m}_0+D_1{m}_1+D_2{m}_2+D_3{m}_3+D_4{m}_4+D_5{m}_5+D_6{m}_6+D_7{m}_7\end{array}$$

令数据 $D_0\sim D_1$ 有些为 $0$ ，有些为 $1$ ，或为其它变量，可构造不同的逻辑函数。

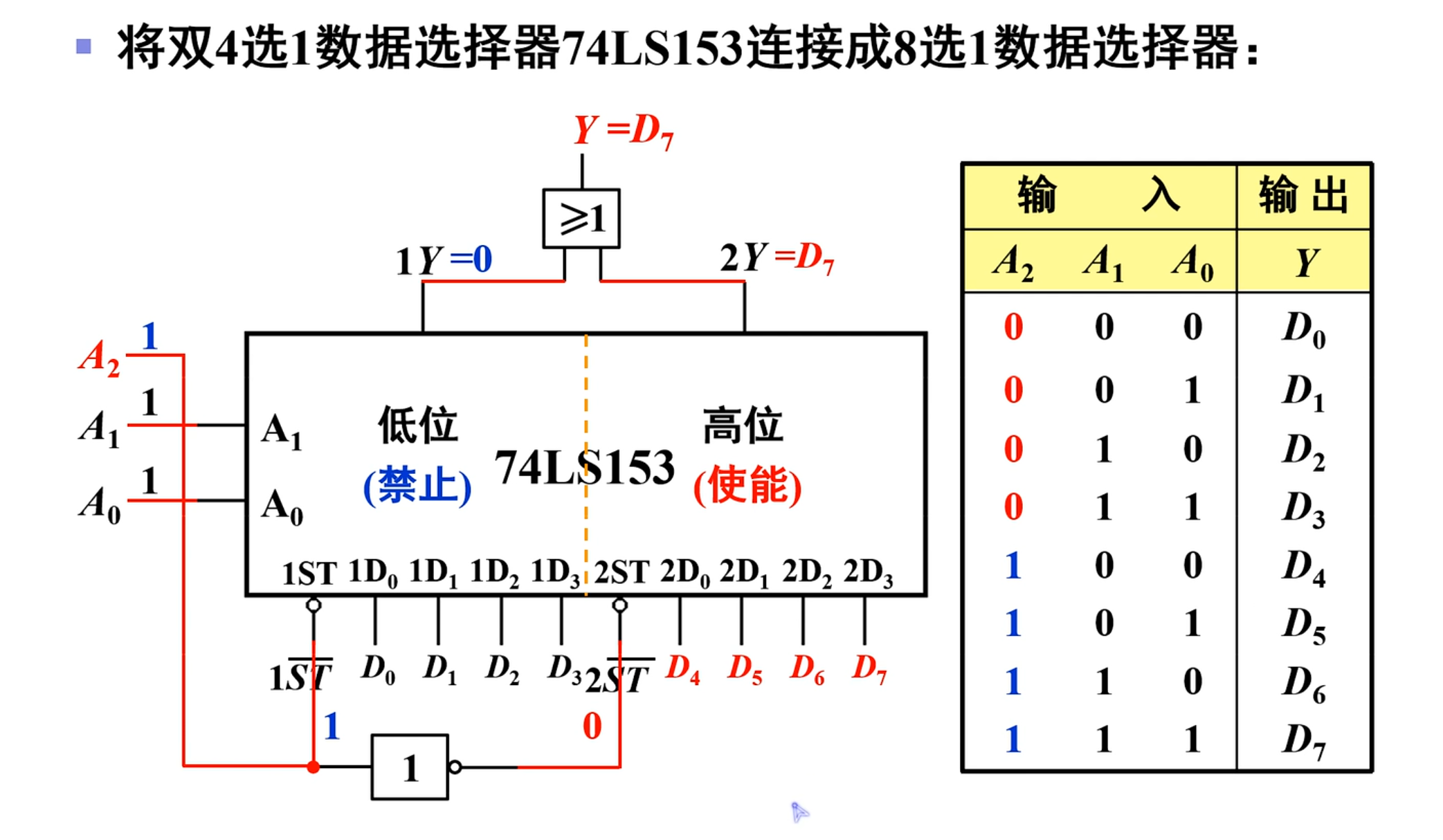
数据选择器的扩展 - 双 4 选 1 连接成 8 选 1

将双 4 选 1 数据选择器 74 LS 153 连接成 8 选 1 数据选择器

数据选择器的扩展 - 两个 8 选 1 连接成 16 选 1

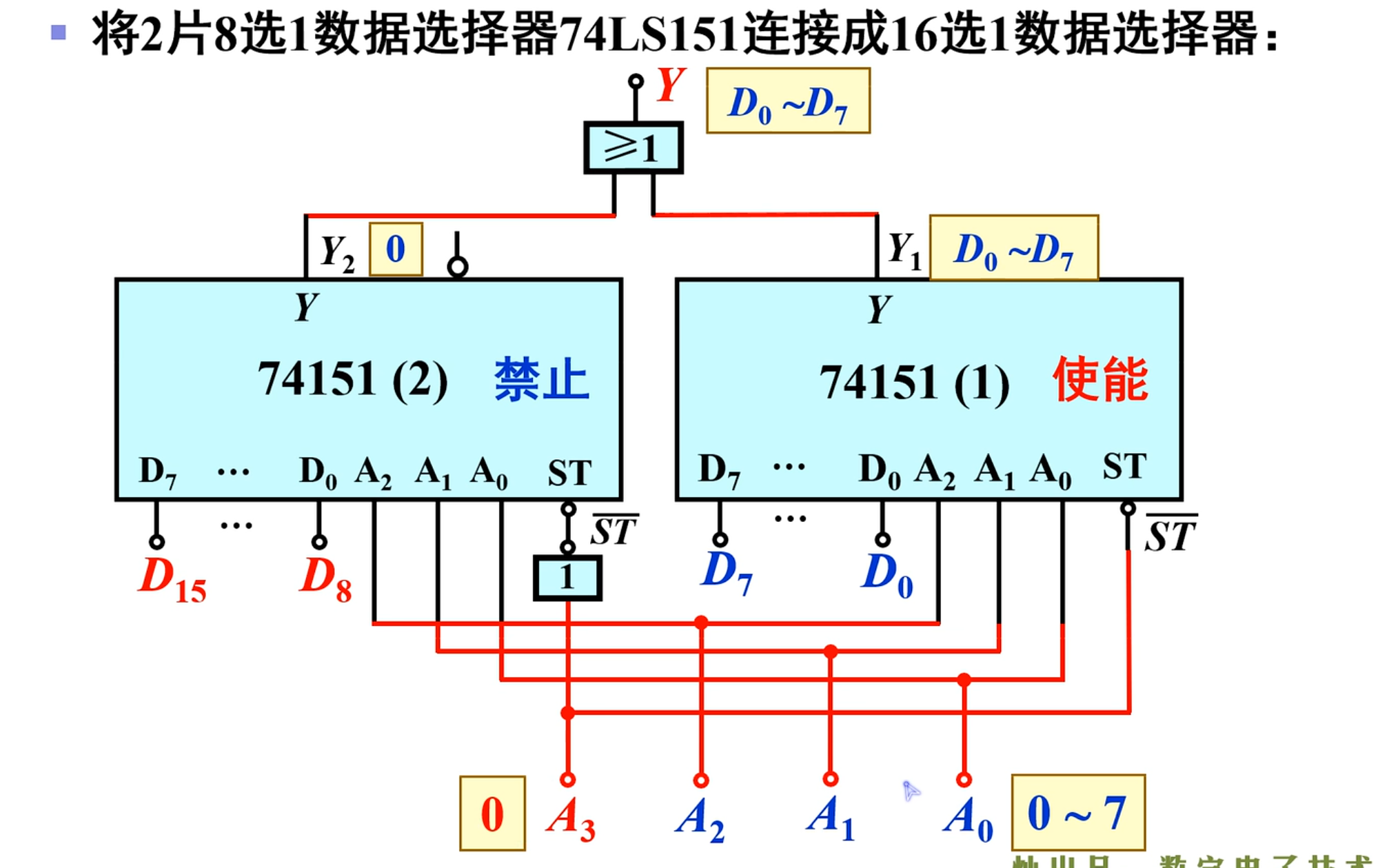
对上面的这个同样按照之前的方法来进行连接，其结果如上图

数据选择器的应用

实现逻辑函数

比如，要实现 $L=\bar{A}B+A\bar{C}$ ，这个是个三变量的

解决方案是将其首先写成最小项的形式

其方法就是缺哪一项，就补哪一项

$$L=\bar{A}B+A\bar{C}=\bar{A}BC+\bar{A}B\bar{C}+AB\bar{C}+A\bar{B}\cdot \bar{C}$$

得到：

$$m_2+m_3+m_4+m_6$$

然后，相应的数据输入端上设置为 $1$ ，没有出现的，设置为 $0$

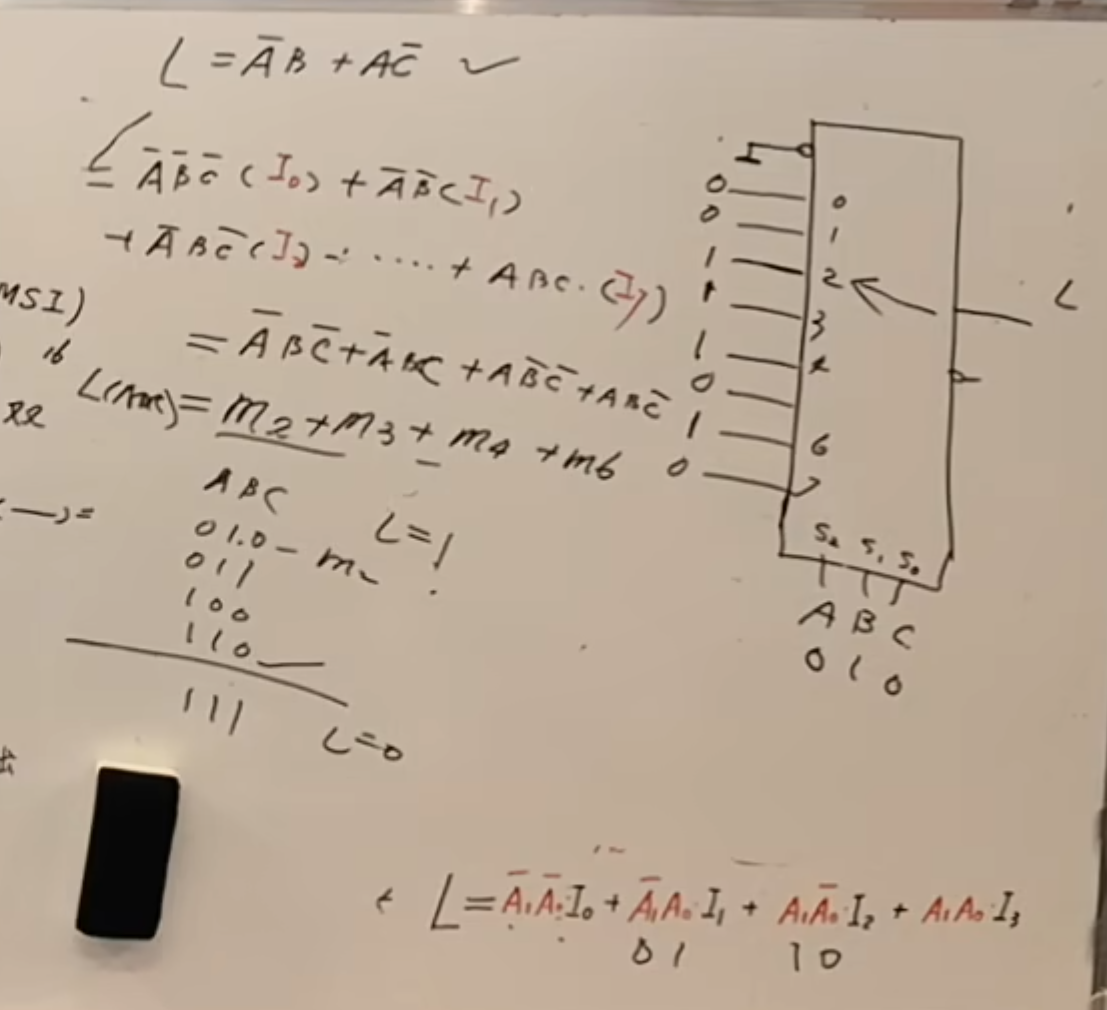
关键是下面这个当有四个变量的时候。再如何逻辑函数的表达。

$$L=AB\bar{C}+BC\bar{D}+\bar{A}BD+A\bar{B}\cdot \bar{C}$$

如果还是使用上面的三变量的数据选择器，那么就需要将一个变量利用使能端进行区分。

那么首先就是将其中的一个变量提取出来，实现对使能端的控制。

$$\begin{array}{rl}L& =AB\bar{C}+BC\bar{D}+\bar{A}BD+A\bar{B}\cdot \bar{C}\\ & =AB\bar{C}+(A+\bar{A})BC\bar{D}+\bar{A}B(C+\bar{C})\bar{D}+A\bar{B}\cdot \bar{C}\\ & =AB\bar{C}+\bar{A}BC\bar{D}+\bar{A}BC\bar{D}+\bar{A}BC\bar{D}+\bar{A}B\bar{C}\cdot \bar{D}+A\bar{B}\cdot \bar{C}\\ & =\bar{A}\cdot \bar{B}\cdot \bar{C}\cdot ()+\bar{A}\cdot \bar{B}C\cdot ()+\bar{A}B\bar{C}\cdot ()+\cdots +ABC\cdot ()\end{array}$$

由于是将 $ABC$ 这三个变量当作最小项

接下来将上面得到的式子中的括号填好即可。括号内的情况只有四种： $0$ 、 $1$ 、 $D$ 、 $\bar{D}$

举个例子：比如说 $\bar{A}BC\bar{D}$ ，由于原式中有这一项，那么在进行填空的时候，就需要填 $\bar{D}$ ，那么在实际接线的时候，接的就是 $\bar{D}$ 。

NOTE

原理是用最小项的性质：

当一个逻辑函数可以写成最小项的形式，那么当输入与其中一个最小项相同的时候，那么输出只能是这个最小项。

相对来说，比较常见的是使用四选一数据选择器：

当然，分析方法是不变的，主要还是先将其换成以 $AC$ 为最小项的形式：

$$\begin{array}{rl}L& =\bar{A}BC+A\bar{C}\cdot \bar{D}+B\bar{C}D\\ & =\bar{A}BC+A\bar{C}\cdot \bar{D}+B\bar{C}D\cdot (A+\bar{A})\\ & =\bar{A}BC+A\bar{C}\cdot \bar{D}+AB\bar{C}D+\bar{A}B\bar{C}D\\ & =\bar{A}\cdot \bar{C}(BD)+\bar{A}C(B)+A\bar{C}(B+\bar{D})+AC(0)\end{array}$$

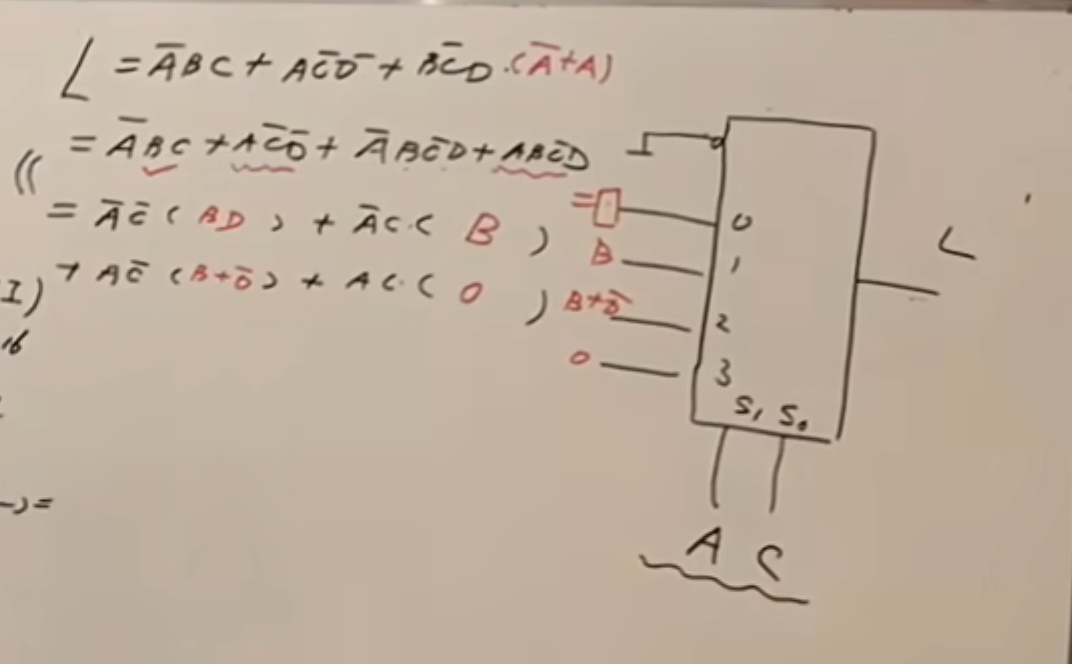
分析方法其实没有什么本质上的区别。

主要是将其中一部分出现的比较多的部分换成最小项的形式

上面是使用的是 $AC$ ，当然也是可以使用 $BC$ 、 $AD$

还可以使用卡诺图的方法来实现。

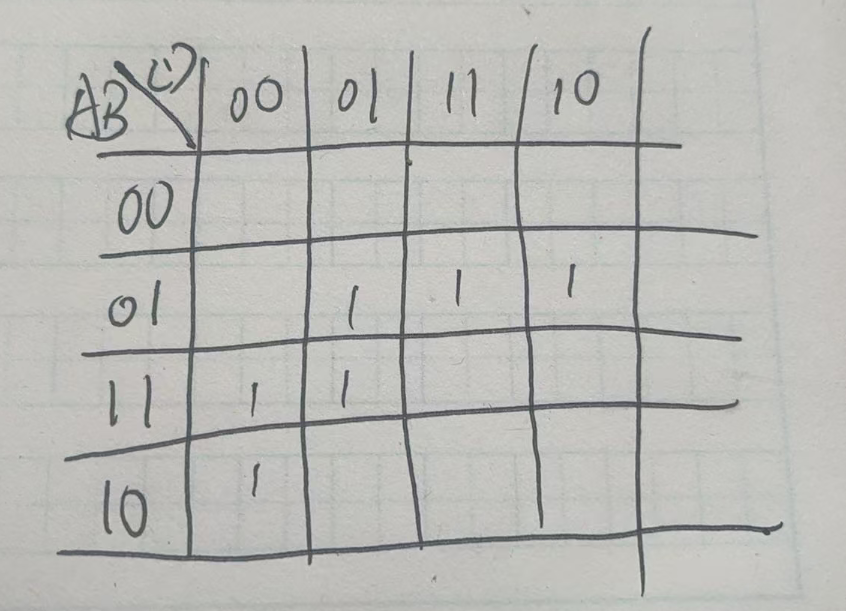
首先将原逻辑表达式画成卡诺图的形式。

然后如果使用 $AB$ 作为最小项。则每一行就对应着每一个数据输入端

如果使用 $CD$ ，那么每一列就对应着一个数据输入端

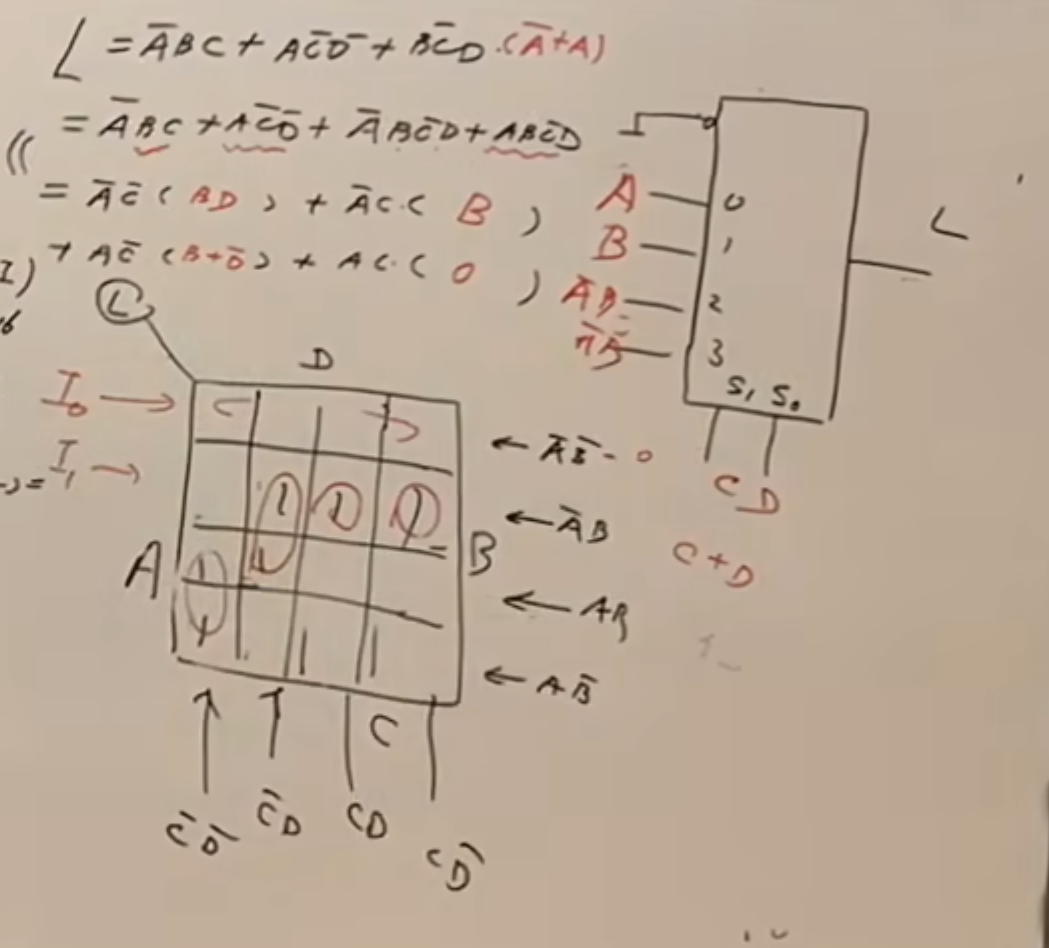
当然，还是要按照卡诺图化简的方法将每一行或者每一列圈出来的，当然，读取的时候也是按照正常的卡努图来读的。

下面是对应另外一个例子：

以 $AB$ 为数据选择端

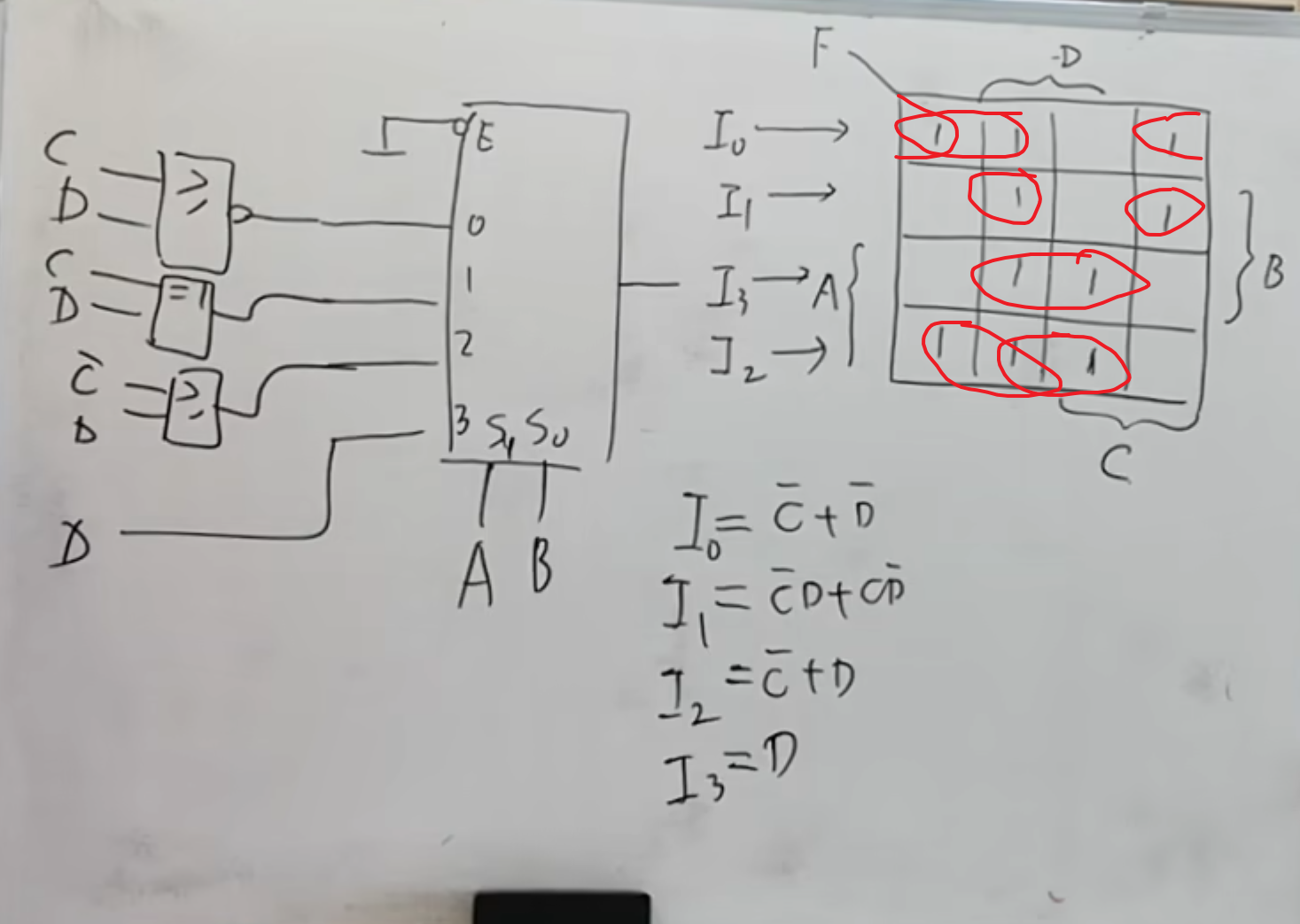
以 $CD$ 为数据选择端

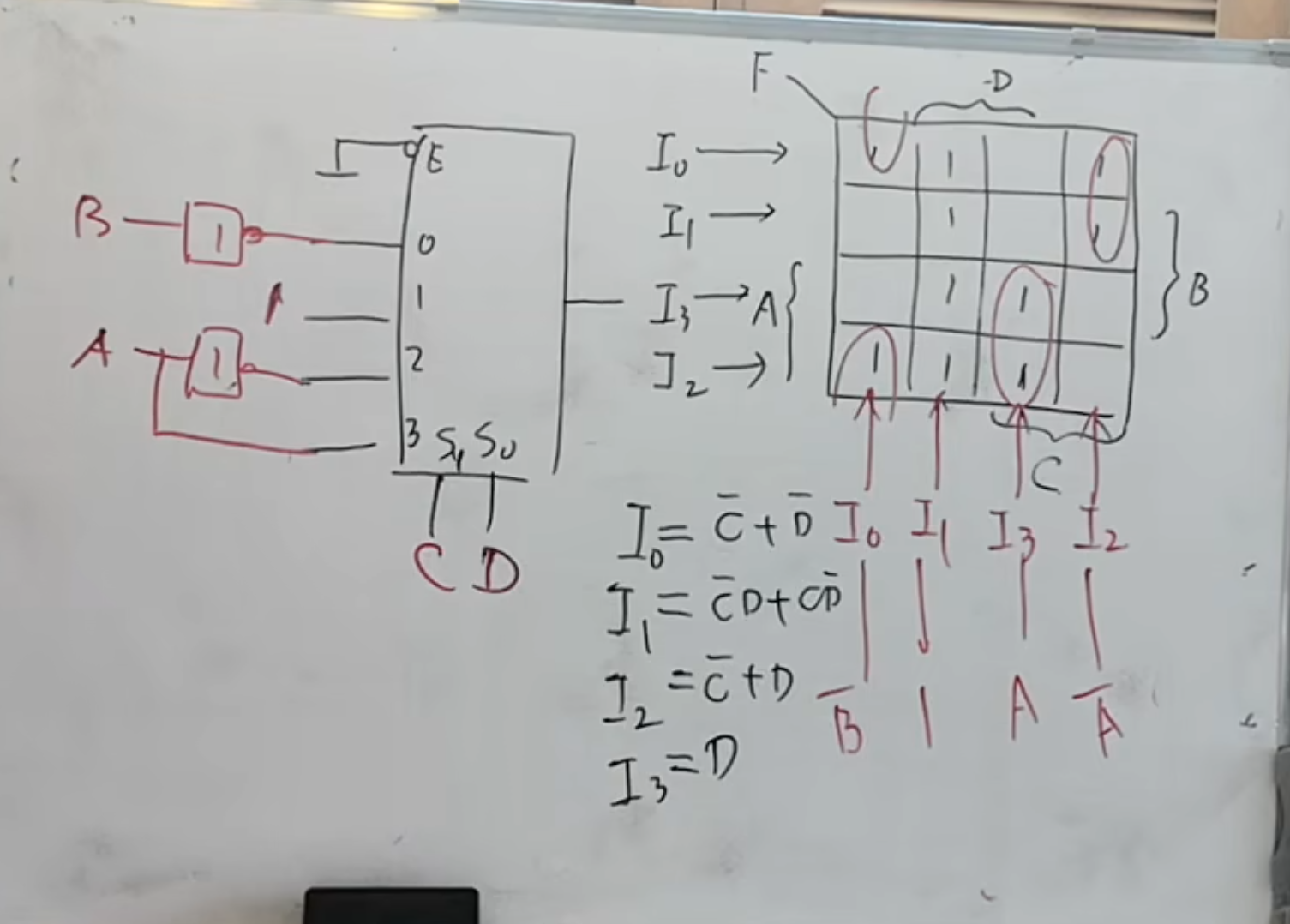
显然以 $CD$ 为数据选择端刚简单一点。

---

当然，也可以使用 $AC$ 作为数据选择端（最小项）

不利于理解。

---

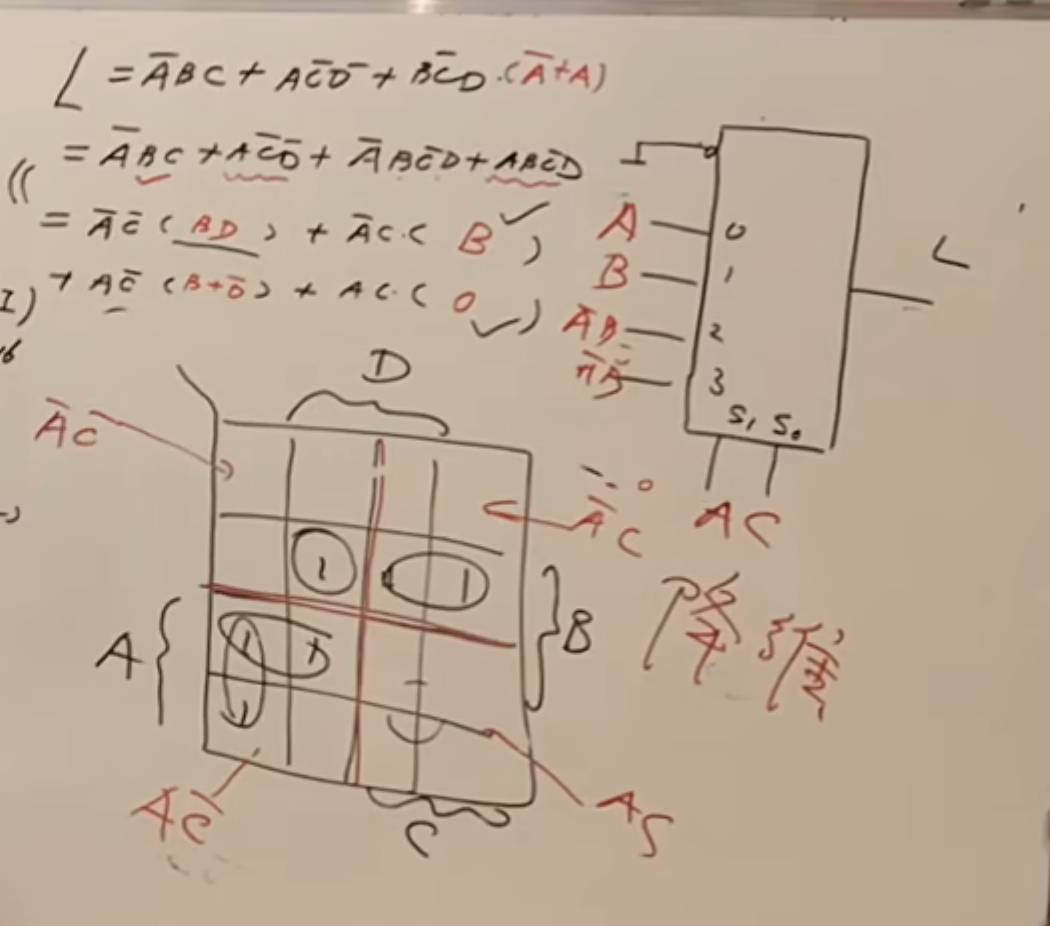
当然，包括 $\overline{AB}$ 、 $\overline{A+B}$ 在内的各种逻辑表达式，都可以使用 4 选 1 数据选择器来实现。

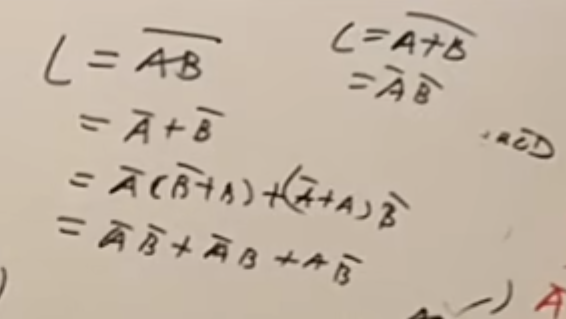
将 4 选 1 扩展到 16 选 1

很明显，16 选 1 至少要使用 4 个 4 选 1 来实现。

实际上，普通的要用 5 个 4 选 1 来实现。

这里的数据选择端上，低位的四个 4 选 1 的数据选择端用低位来连接，高位的哪一个 4 选 1 数据选择端用高位来连接，如上面图中所示。

当然，除了上面这种使用 5 个 4 选 1 数据选择器。也可以使用控制使能端的方法来实现对输出结果的控制。

还是假设输入的是 $1101$ ，那么 $AB$ 的值是 $11$ ，而 $AB$ 的取值一共有 4 种情况。分别是 $00、01、10、11$ ，那么就可以使用使用一个 2 - 4 的译码器，分别来控制四个 4 选 1 的数据选择器的使能端。同样可以得到相同的结果。

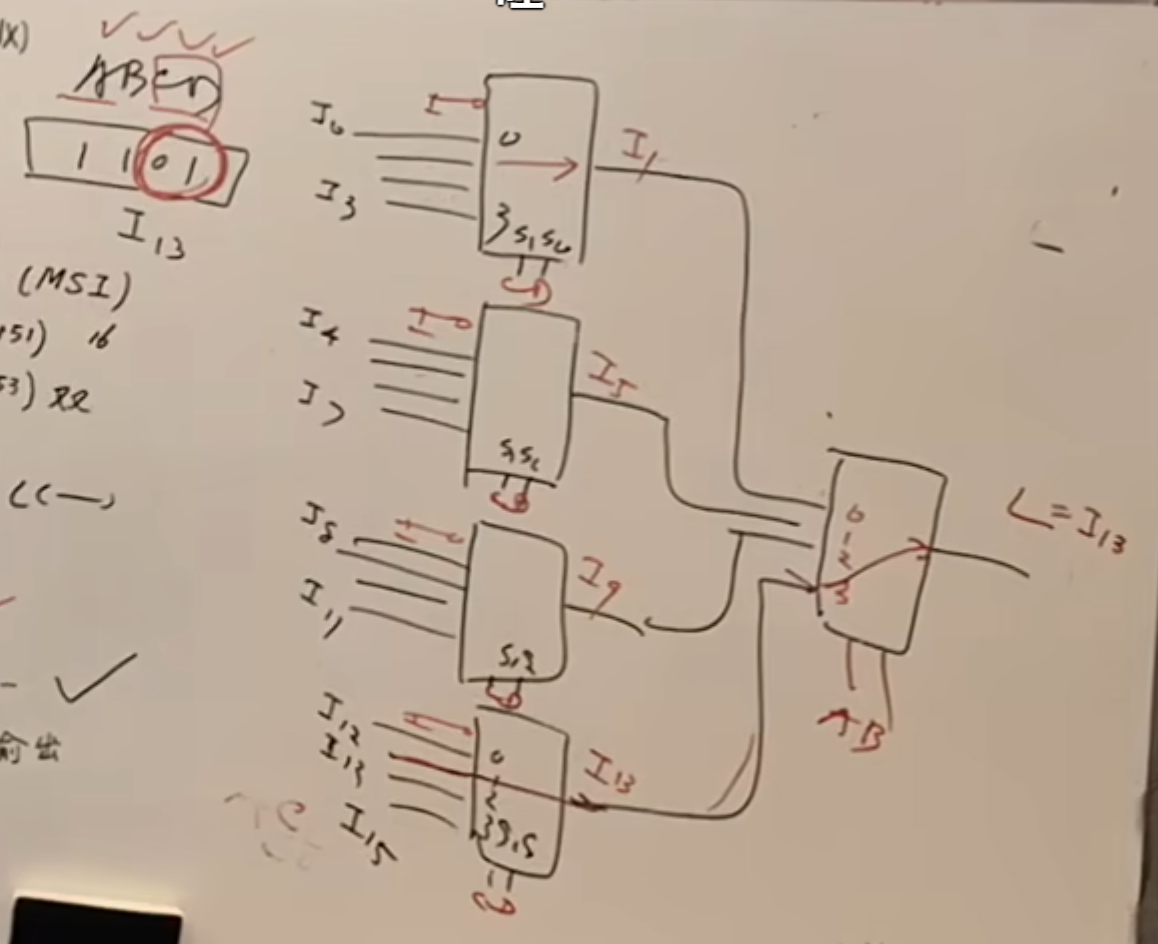
并行输入串行输出

其主要实现的东西是：将一组二进制数，按照想要的顺序（CBA 不同波形组合）输出出去。

IMPORTANT

注意高位、低位的顺序。在这里 $A$ 是高位。 $C$ 是低位

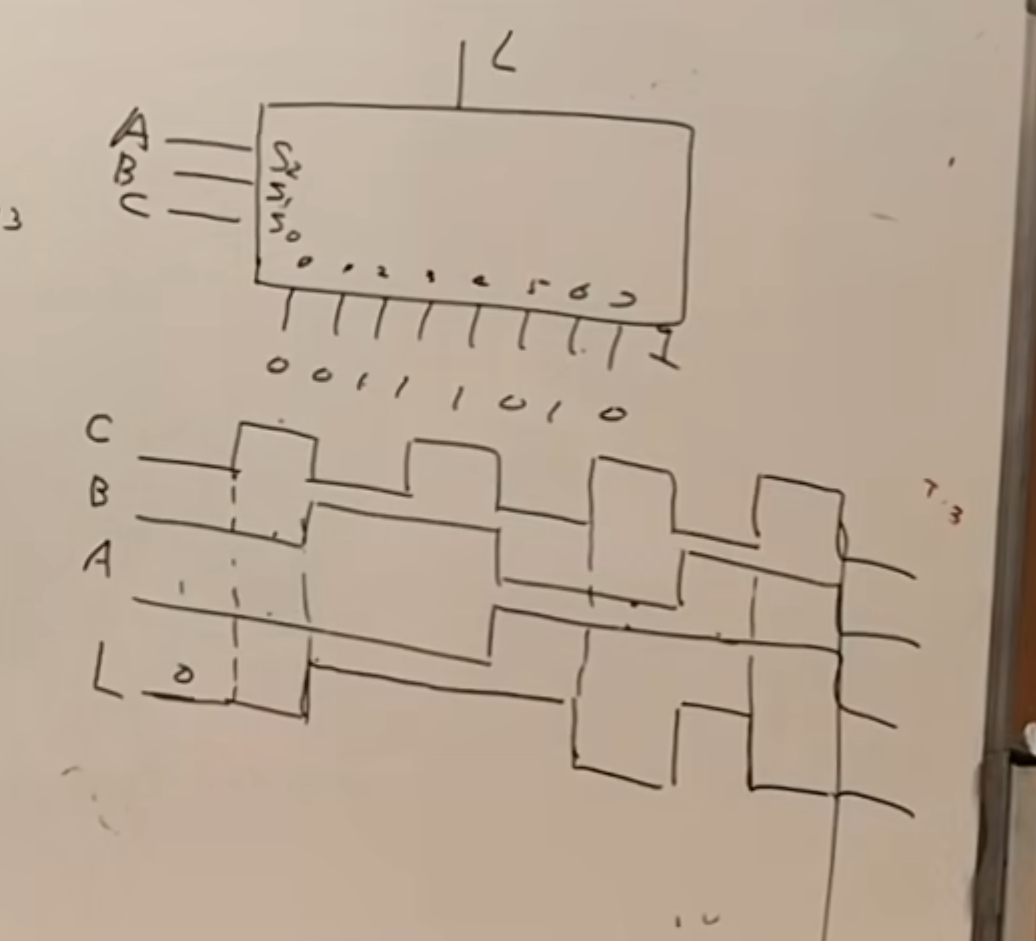
这里就是实现了数据的串行、并行转换

数据分配器

NOTE

根据地址信号的要求，将一路输入数据分配到多路输出中的其中一路作为输出的逻辑电路，称为数据分配器（Demultiplexer），简称为 DMUX

这个刚好跟数据选择器是一个镜像（这个是一个输入，四个输出）

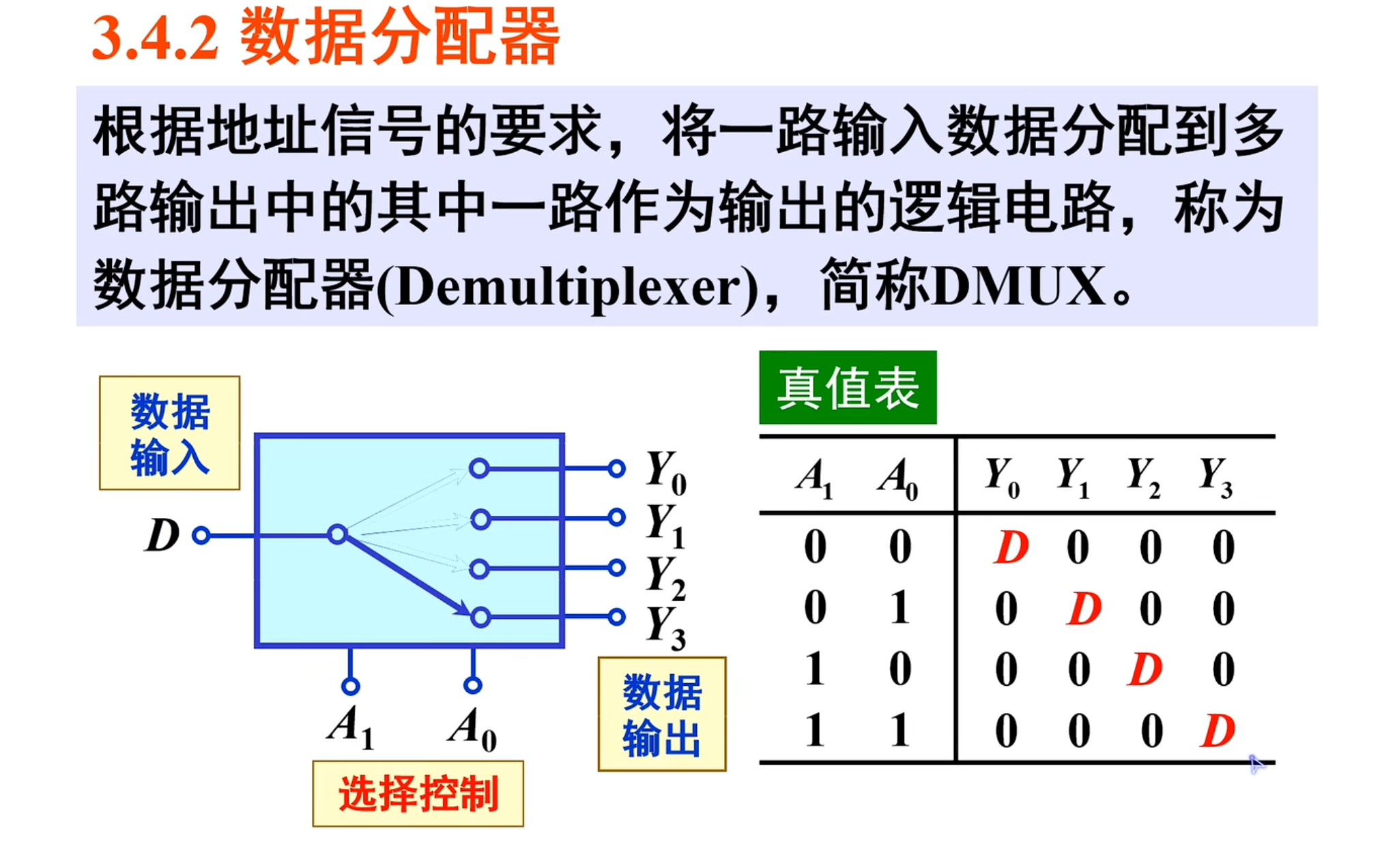
在上面真值表中，使用的是 $D$ ，而不是 $1$ 或者 $0$ ，原因在于其取值是根据 $D$ 的取值来的。

下面是其集成芯片，但是需要注意的是，数据分配器是没有相应的芯片的，而是用功能差不多的译码器实现的，将译码器的一些端进行处理一下就得到了**数据选择器

3 线-8 线译码器 74 LS 138 可以构成 1 路- 8 路数据分配器。 $A_2$ 、 $A_1$ ， $A_0$ 为地址信号输入端， $\overline{Y_0}\sim \overline{Y_7}$ 为数据输出端，三个使能 $\overline{S{T}_A}$ 、 $\overline{S{T}_B}$ 、 $\overline{S{T}_C}$ 中的任一个都可作数据 $D$ 输入端。

而可以得到有两种接法：

下面这个是第一个：

然后是第二个：

用中规模集成电路实现组合逻辑函数

主要是用二进制译码器实现组合逻辑电路，以及用数据选择器实现组合逻辑电路

首先要理解什么是电路实现：

用一个例子来说明：

引例：使用合适的逻辑电路实现函数 $F=AB+BC+AC$ 。

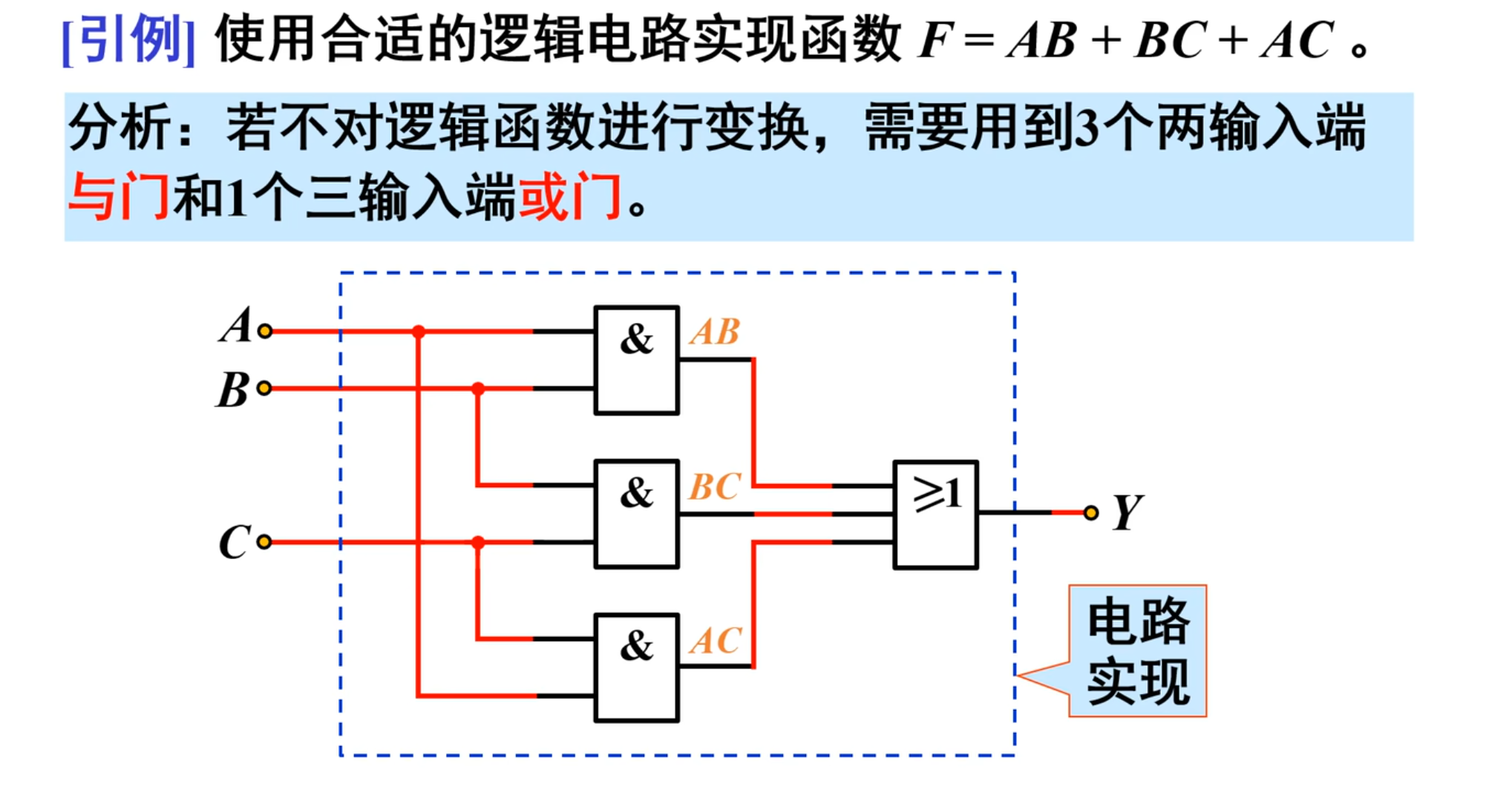
首先是不对逻辑函数进行变换，其需要用三个与门和一个三输出的或门

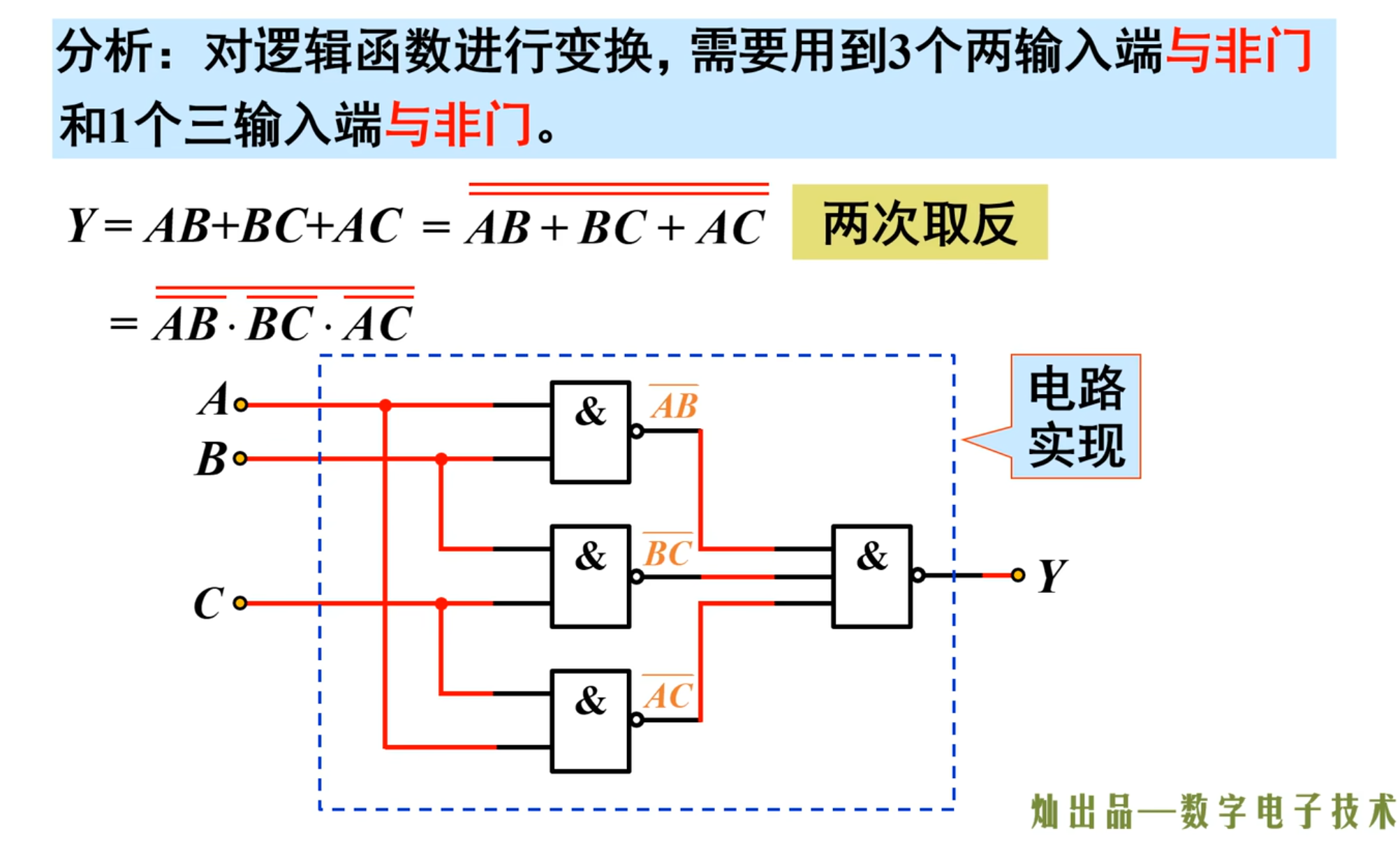
那么，如果要对逻辑函数进行变换

将原函数进行两次取反，可以得到：

$$\begin{array}{rl}Y& =AB+BC+AC\\ & =\overline{\stackrel{―}{AB+BC+AC}}\\ & =\overline{AB\cdot BC\cdot AC}\end{array}$$

这样得到的输入只需要用到 3 个两输入端与非门，以及 1 个三输入与非门

下面是它的电路实现：

当然，除了上面的普通与非门，也可以用二进制译码器来实现

所以，问题就在于如何使用这些译码器、数据选择器来实现上面说到的功能

NOTE

如果要选用“二进制译码器”或者“数据选择器”，其实就是要确定“二进制译码器”或“数据选择器”输入端与待求函数输入信号 $A、B、C$ ，输出端与输出信号 $Y$ 之间的连接关系，也就是求之间的逻辑

二进制译码器实现组合逻辑函数

NOTE

其本质上是：

由于 $n$ 位二进制译码器可提供 $2^n$ 个最小项的输出，而任一个逻辑函数都可变换为最小项之和的标准与或式，因此利用译码器和门电路可实现单输出及多输出组合逻辑电路。

IMPORTANT

当译码器输出低电平有效的时候，选用与非门

当译码器输出高电平有效的时候，选用或门

下面是基本步骤：

1. 选择集成二进制译码器（不一定是 138）

2. 写出待求函数的标准与非-与非式（两次取反）

3. 确定待求函数变量和译码器输入端之间的关系

4. 选择合适的门电路，画出连线图

下面通过例题来说明如何实现：

注意看，上面的这个表达式不是最简单的，其可以换成 $Y=AB+C$

但是我们不需要换，因为在于我们还要二次取反，所以并不需要化简。

下面是正式的步骤：

首先，要根据逻辑函数选择译码器

很明显，有三个输入，所以要选择 3 线-8 线译码器（138）

然后，就是将函数式换成标准的与或式

$$\begin{array}{rl}F& =\bar{A}\bar{B}C+AB\bar{C}+C(\bar{A}+A)(\bar{B}+B)\\ & =\bar{A}\bar{B}C+AB\bar{C}+\bar{A}BC+A\bar{B}C+ABC\\ & =m_1+m_3+m_5+m_6+m_7\end{array}$$

除了上面这种直接写出标准与或式的方法，还可以利用卡诺图来实现：

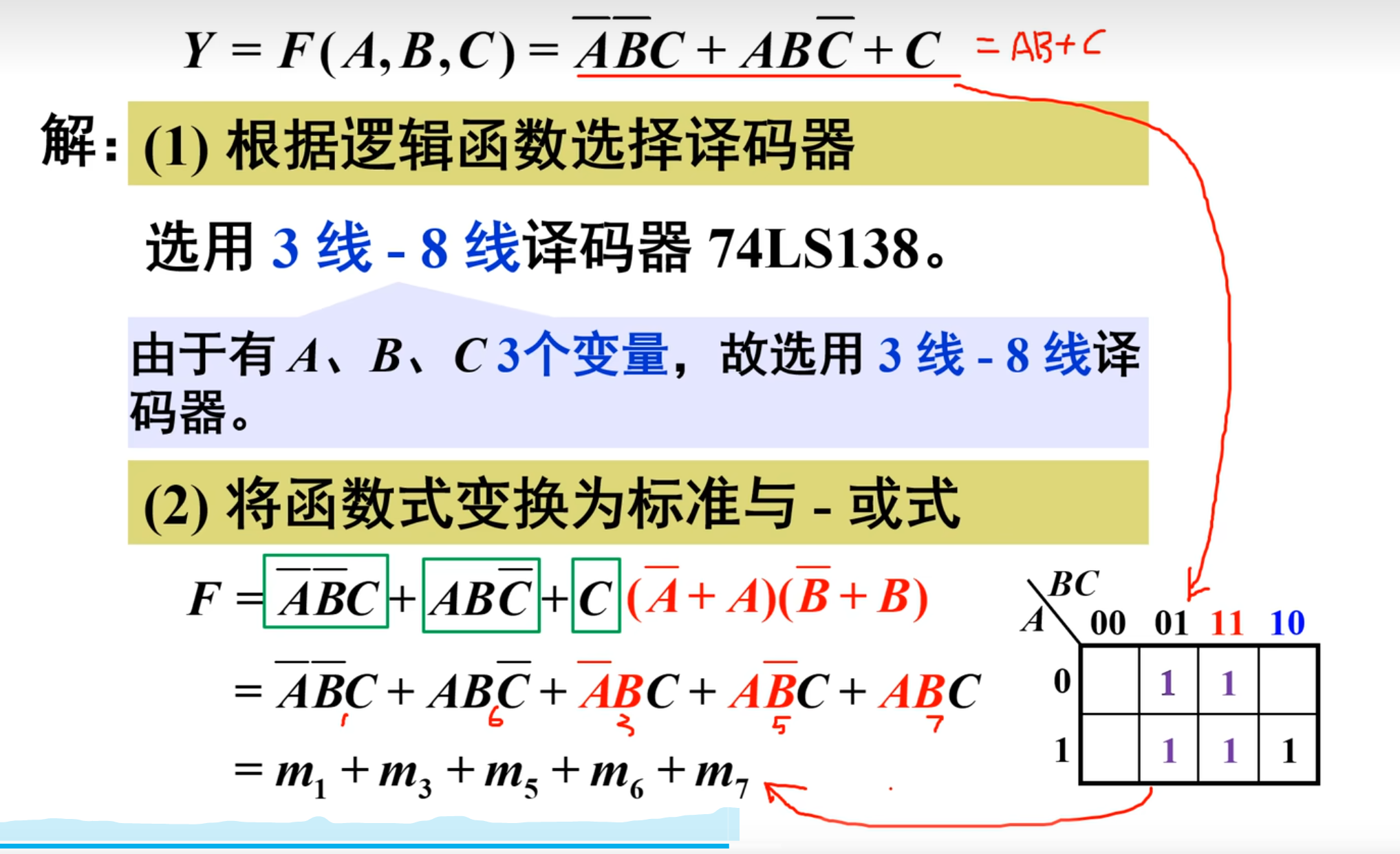
然后进行两次取反，得到标准的与非表达式：

$$\begin{array}{rl}F& =m_1+m_3+m_5+m_6+m_7\\ & =\overline{\stackrel{―}{m_1}\cdot \stackrel{―}{m_3}\cdot \stackrel{―}{m_5}\cdot \stackrel{―}{m_6}\cdot \stackrel{―}{m_7}}\end{array}$$

（上面是以 $A、B、C$ 作为变量 ）

然后是待求函数变量和译码器输入端之间的关系：

138 是输出低电平有效， $\overline{Y_i}=\overline{m_i}$ ，（以 $A_2、A_1、A_0$ 作为变量 ）

回顾一下功能表：

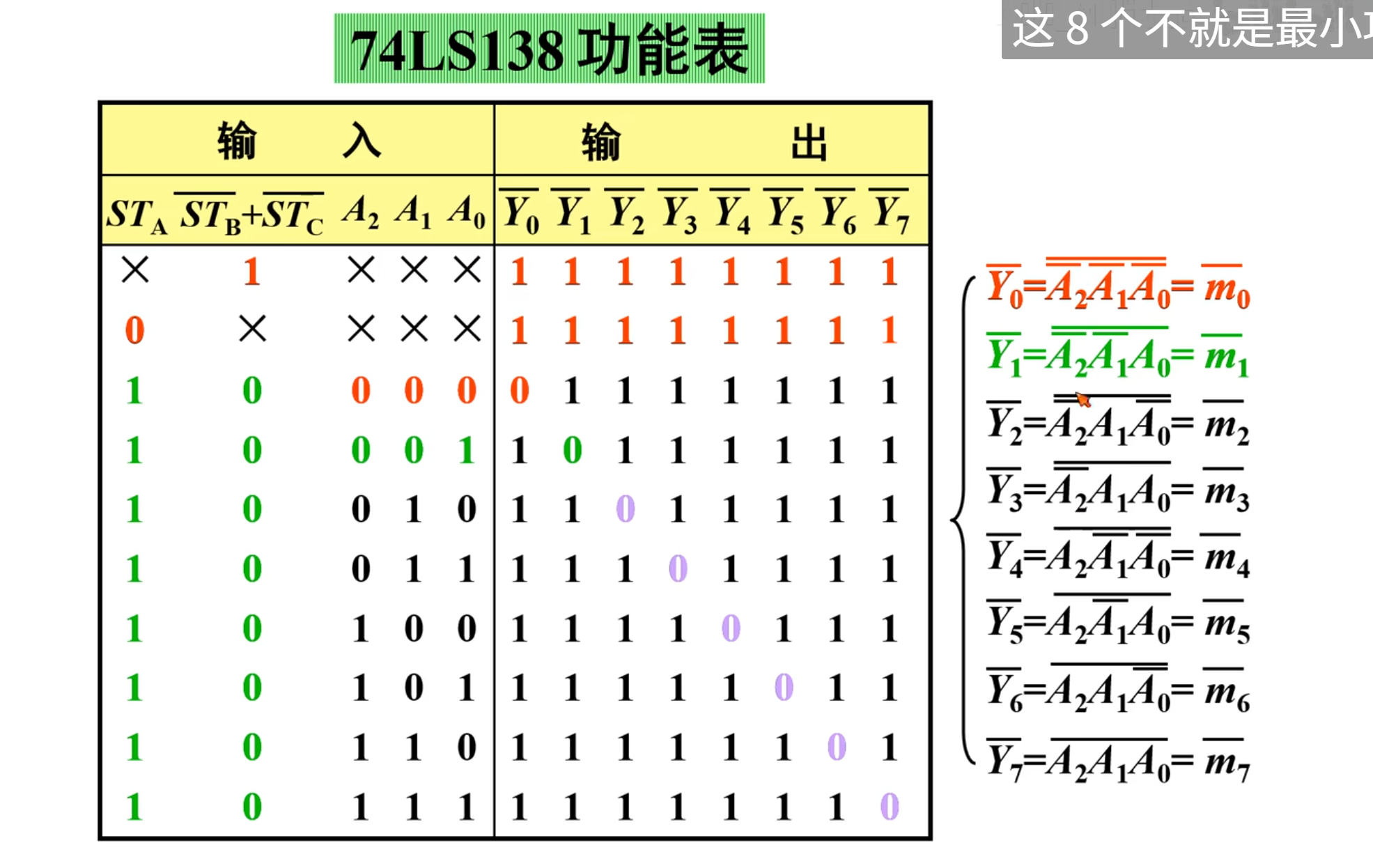
我们在上面已经知道了 $F$

$$\begin{array}{rl}F& =m_1+m_3+m_5+m_6+m_7\\ & =\overline{\stackrel{―}{m_1}\cdot \stackrel{―}{m_3}\cdot \stackrel{―}{m_5}\cdot \stackrel{―}{m_6}\cdot \stackrel{―}{m_7}}\end{array}$$

然后令 $A_2=A$ ， $A_1=B$ ， $A_0=C$ ，那么就可以得到：

$$F=\overline{\stackrel{―}{Y_1}\cdot \stackrel{―}{Y_3}\cdot \stackrel{―}{Y_5}\cdot \stackrel{―}{Y_6}\cdot \stackrel{―}{Y_7}}$$

这样就找到了 $F$ 跟 $Y$ 之间的关系

而得到的结果中的 $\overline{Y_1}、\overline{Y_3}、\cdots 、\overline{Y_7}$ 就是 138 的输出，而最后的结果就是将其与非到一起即可。

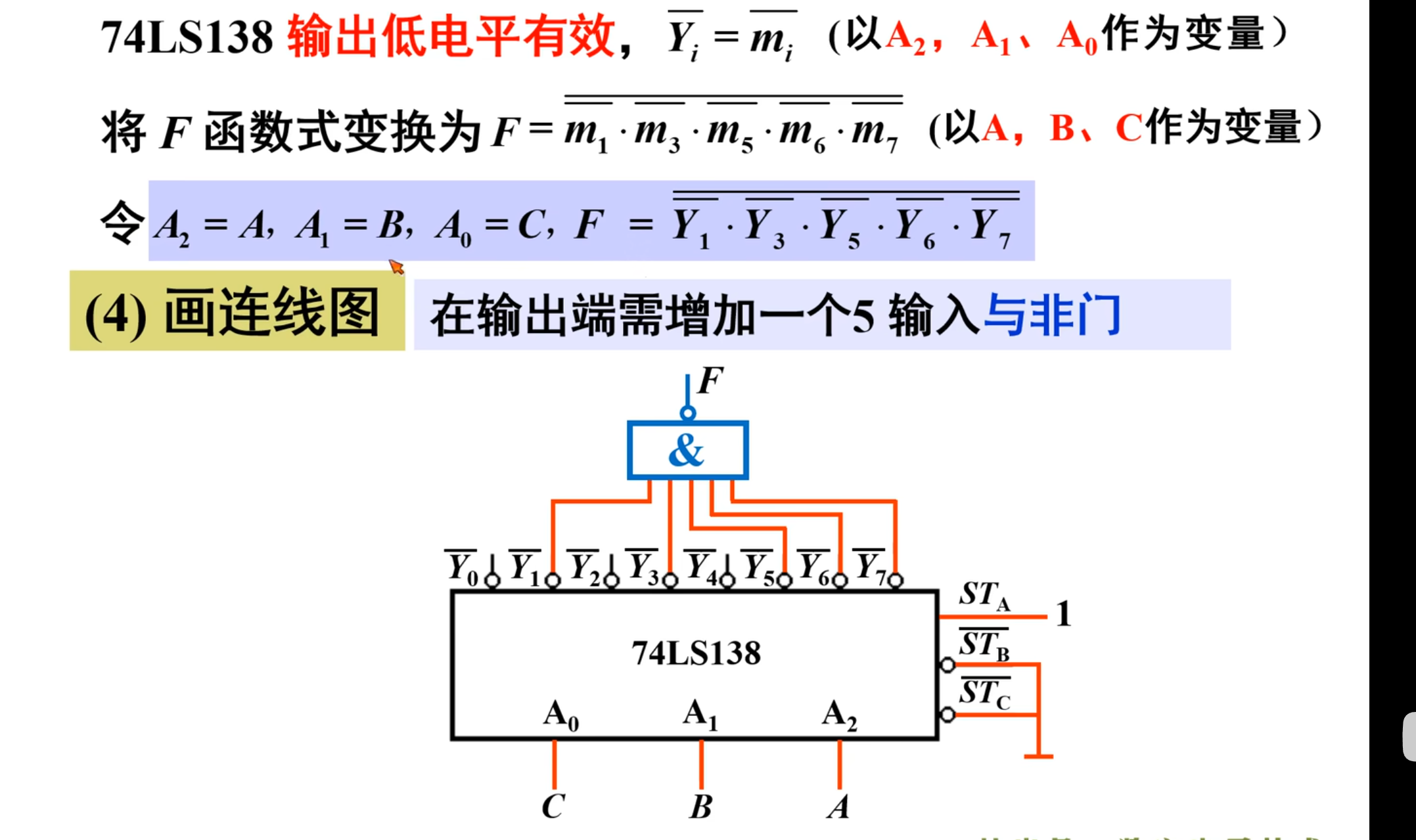
上面的图，就是最后的连线结果

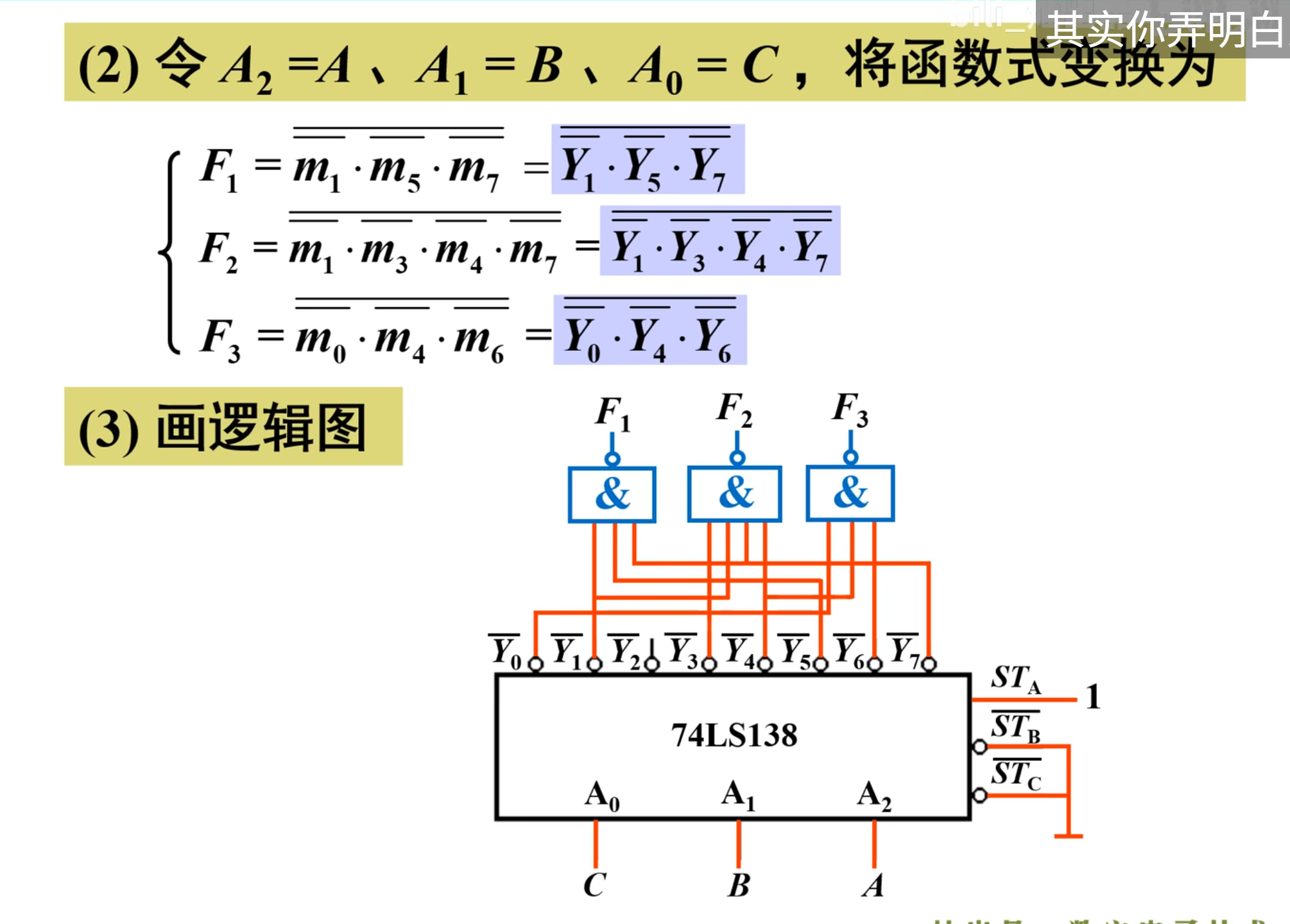
再来一个例题：

用卡诺图写出输出逻辑函数的最小项表达式

$$\{\begin{array}{l}{F}_1=\bar{A}\bar{B}C+A\bar{B}C+ABC=m_1+m_5+m_7\\ F_2=\bar{A}\bar{B}C+\bar{A}BC+A\bar{B}\bar{C}+ABC=m_1+m_3+m_4+m_7\\ F_3=\bar{A}\bar{B}\bar{C}+A\bar{B}\bar{C}+AB\bar{C}=m_0+m_4+m_6\end{array}$$

然后换成与非表达式：

$$\begin{array}{r}\{\begin{array}{l}{F}_1=\overline{\stackrel{―}{m_1}\cdot \stackrel{―}{m_5}\cdot \stackrel{―}{m_7}}\\ F_2=\overline{\stackrel{―}{m_1}\cdot \stackrel{―}{m_3}\cdot \stackrel{―}{m_4}\cdot \stackrel{―}{m_7}}\\ F_3=\overline{\stackrel{―}{m_0}\cdot \stackrel{―}{m_4}\cdot \stackrel{―}{m_6}}\end{array}\end{array}$$

然后则是令 $A_2=A$ ， $A_1=B$ ， $A_0=C$ ，将函数式变换为：

IMPORTANT

这里需要注意，在变换变量的时候，要注意其之间的对应关系，通常是要反过来取值的

在这里， $A_2$ 是高位

此处需要额外注意

$$\begin{array}{r}\{\begin{array}{l}{F}_1=\overline{\stackrel{―}{m_1}\cdot \stackrel{―}{m_5}\cdot \stackrel{―}{m_7}}=\overline{\stackrel{―}{Y_1}\cdot \stackrel{―}{Y_2}\cdot \stackrel{―}{Y_7}}\\ F_2=\overline{\stackrel{―}{m_1}\cdot \stackrel{―}{m_3}\cdot \stackrel{―}{m_4}\cdot \stackrel{―}{m_7}}=\overline{\stackrel{―}{Y_1}\cdot \stackrel{―}{Y_3}\cdot \stackrel{―}{Y_4}\cdot \stackrel{―}{Y_7}}\\ F_3=\overline{\stackrel{―}{m_0}\cdot \stackrel{―}{m_4}\cdot \stackrel{―}{m_6}}=\overline{\stackrel{―}{Y_0}\cdot \stackrel{―}{Y_4}\cdot \stackrel{―}{Y_6}}\end{array}\end{array}$$

然后就是画出逻辑图：

再来一个例三：

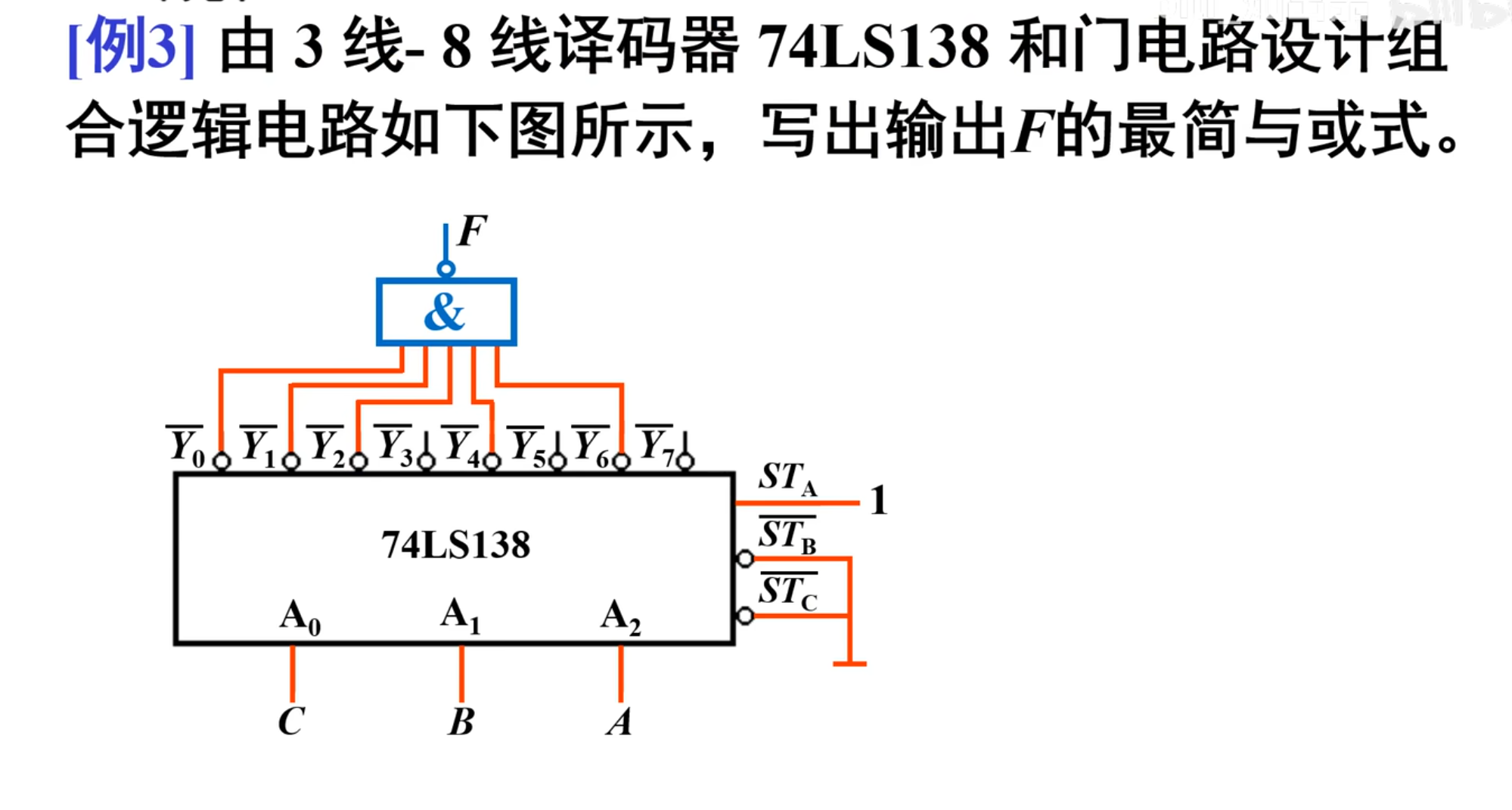
这个跟之前的题目是刚好反过来的。

解决方法是：

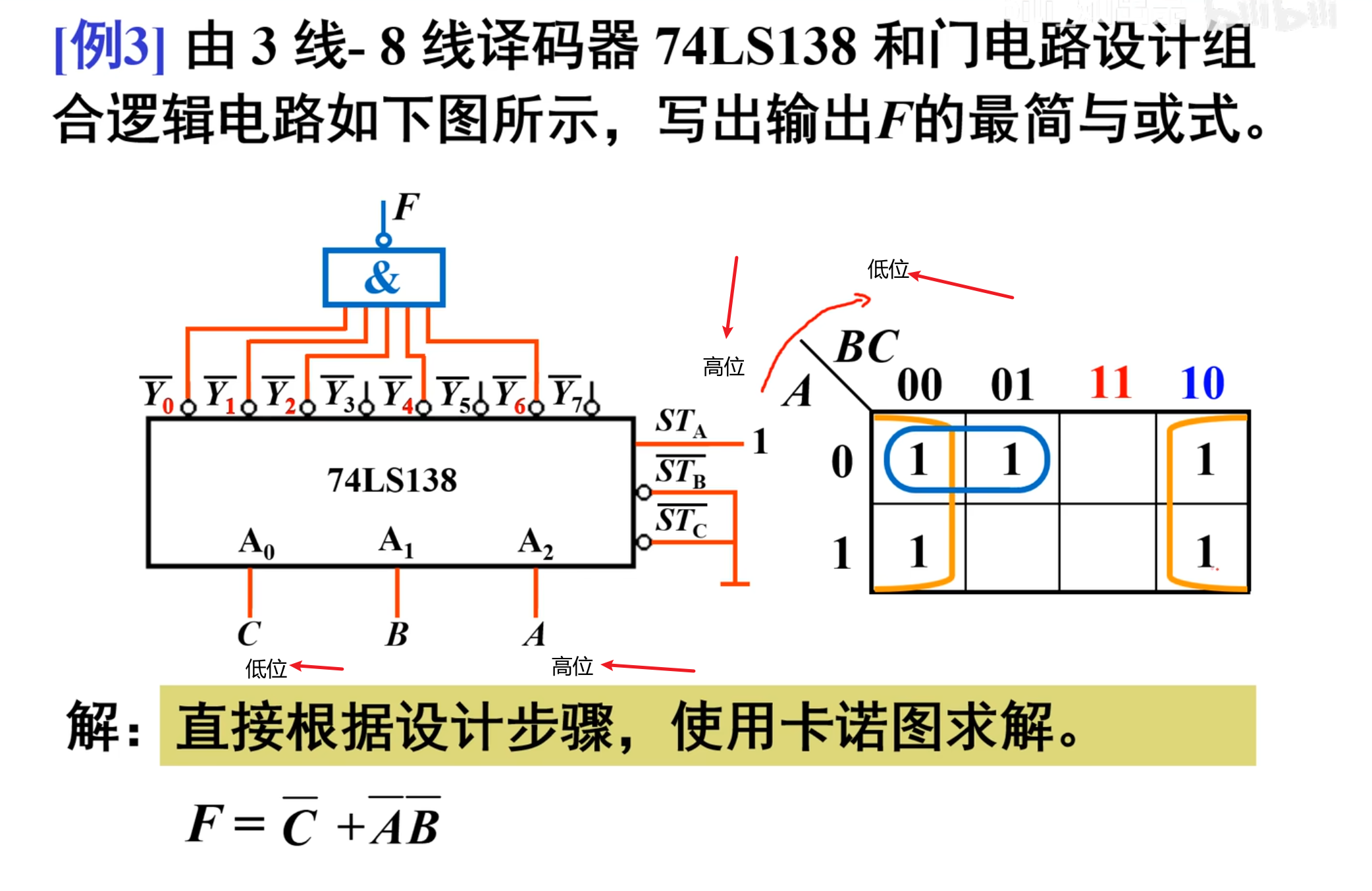
直接根据设计步骤，使用卡诺图求解：

直接看有几个输出的 $\overline{Y_i}$ ，将其对应的 $1$ 写到卡诺图上

观察上面的图中是 $(0,1,2,4,6)$ ，所以在卡诺图上对应的位置上写上 $1$

然后是根据卡诺图来进行化简结果

IMPORTANT

注意，在画卡诺图的时候，不能写反，在 138 上，是 $A_2$ 是高位， $A_0$ 是低位，相应的在卡诺图上左边的是高位，右边依次是低位，一定要注意顺序

数据选择器实现组合逻辑电路

首先来回顾一下，数据选择器的输出是标准与或式，其中包含地址变量的全部最小项

基本步骤：

1. 根据 $n=k-1$ 或 $n=k$ 来确定数据选择器的型号；当然，在这里的 $n$ 是选择器地址输入端的个数， $k$ 是函数的变量个数。（为什么会有 $n=k-1$ ，是因为这个是一种比较复杂的解决方法，用的是降维的方法 ）

2. 然后是写出函数的标准与或式和选择器的输出信号表达式

3. 对这两个表达式进行比较（卡诺图），确定选择器各个输入变量的表达式 （选择器输入端跟待求函数的输入变量之间是如何连接的，以及数据选择器的输出端与待求函数的输出之间的连接关系）

4. 完成之后，根据采用的数据选择器和求出的表达式画出连线图

不降维的解法

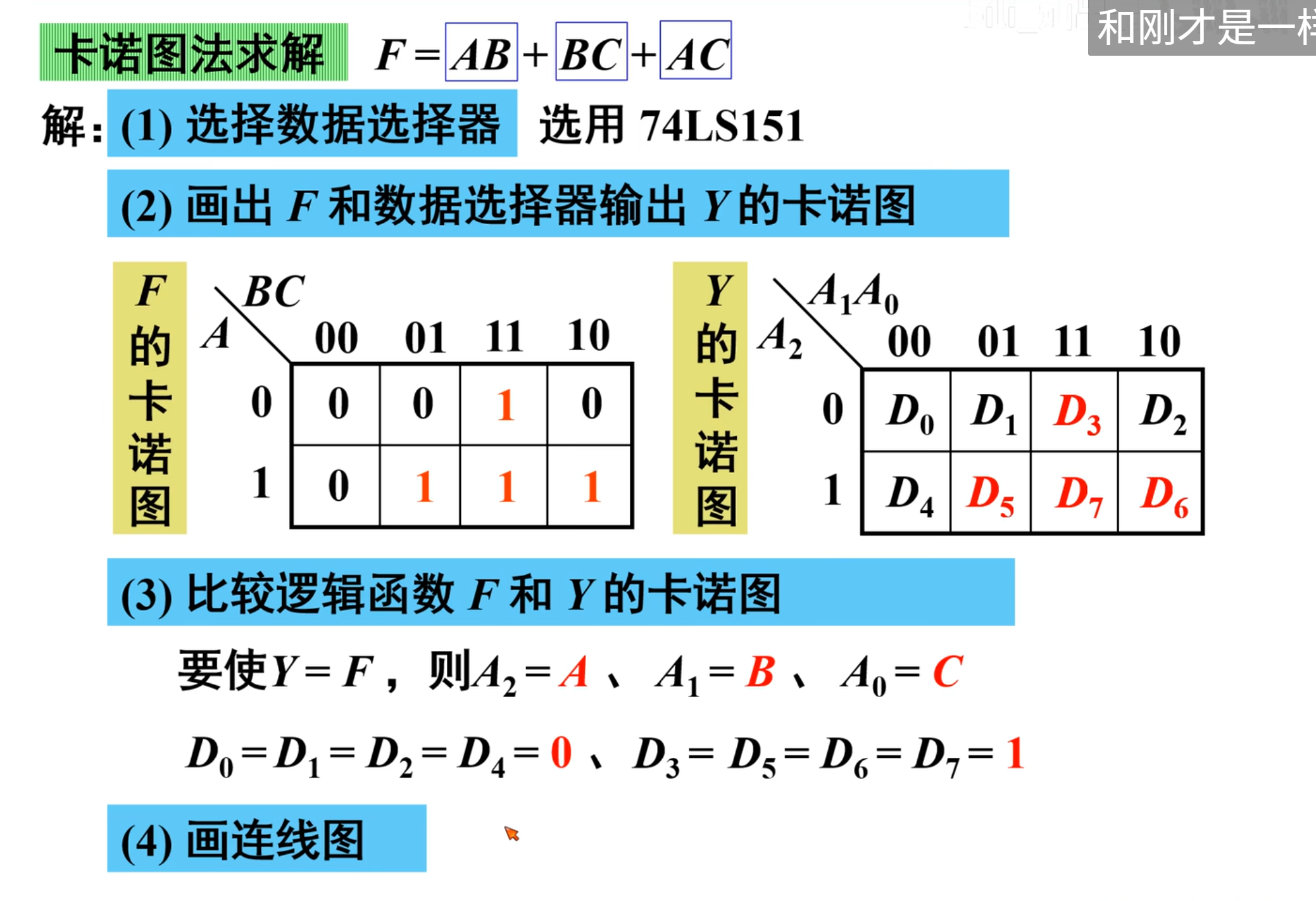
下面使用一个比较简单的例题来说明：

首先是代数法来求解：

写出最小项表达式为：

$$Y=AB+BC+AC=\bar{A}BC+A\bar{B}C+AB\bar{C}+ABC=m_3+m_5+m_6+m_7$$

然后再写出数据选择器（8 选 1）的输出表达式，在上图中。

然后将待求函数的表达式与数据选择器的表达式进行比较：

当然，在此之前，需要先令 $A_2=A$ ， $A_1=B$ ， $A_0=C$

可以得到：

$$\begin{array}{rl}Y& =D_0\bar{A}\cdot \bar{B}\cdot \bar{C}+D_1\bar{A}\cdot \bar{B}\cdot C+D_2\bar{A}B\bar{C}+D_3\bar{A}BC\\ & +D_{4}A\bar{B}\cdot \bar{C}+D_{5}A\bar{B}C+D_{6}AB\bar{C}+D_{7}ABC\end{array}$$

通过对比可以得到：

得到：

$$\begin{array}{r}\{\begin{array}{l}{D}_0=D_1=D_2=D_4=0\\ D_3=D_5=D_6=D_7=1\end{array}\end{array}$$

这样就得到了数据选择部分的取值，最后是画图

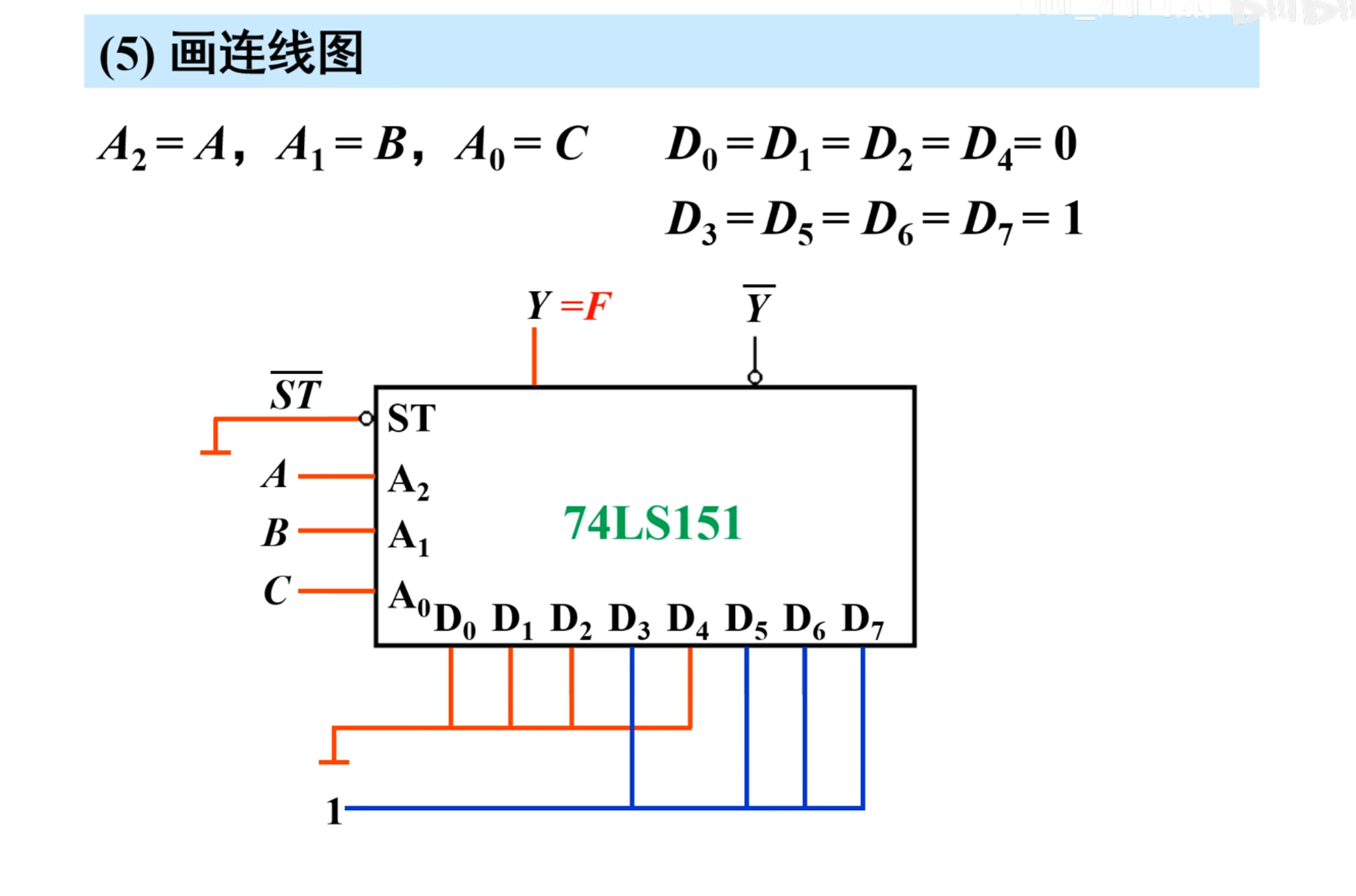
接下来是用卡诺图来求解

用卡诺图的方法要更简单一些

关键点在于要画对 $F$ 的卡诺图，然后则是 $Y$ 卡诺图的顺序要正确，记住 $A$ 和 $A_2$ 都是高位即可

然后一一对应就可以得到结果。

---

降维的解法

IMPORTANT

降维是要降掉最低位

下面是需要降维的使用数据选择器

NOTE

其实上就是用 4 选 1（153）来实现三变量的函数表达式。

因为 4 选 1 只有两位地址输入端

也就是 $n=k-1$ 的时候

当然，求解方法其实没有什么很大的不同，关键点在于降维的那部分

依然是写出函数的标准与或式：

$$F=\bar{A}BC+A\bar{B}C+AB\bar{C}+ABC$$

当然，还有 4 选 1 数据选择器的表达式：

$$Y=D_0\overline{A_1}\cdot \overline{A_0}+D_1\overline{A_1}{A}_0+D_2{A}_1\overline{A_0}+D_3{A}_1{A}_0$$

很明显，现在不够用，所以下面的部分就是重点：

要确定输入变量和地址码之间的关系：

方法 1 就是公式拼凑法

首先要做的是找到对应关系：

令 $A_1=A$ ， $A_0=B$ ，得到 $Y$

$$Y=D_0\bar{A}\cdot \bar{B}+D_1\bar{A}B+D_{2}A\bar{B}+D_{3}AB$$

然后换一下位置得到：

$$Y=\bar{A}\cdot \bar{B}{D}_0+\bar{A}B{D}_1+A\bar{B}{D}_2+AB{D}_3$$

我们的目的是对应 $Y=F$

可以得到， $D_0=0$ ， $D_1=C$ ， $D_2=C$ ， $D_3=\bar{C}+C=1$

然后接下来就是画图：

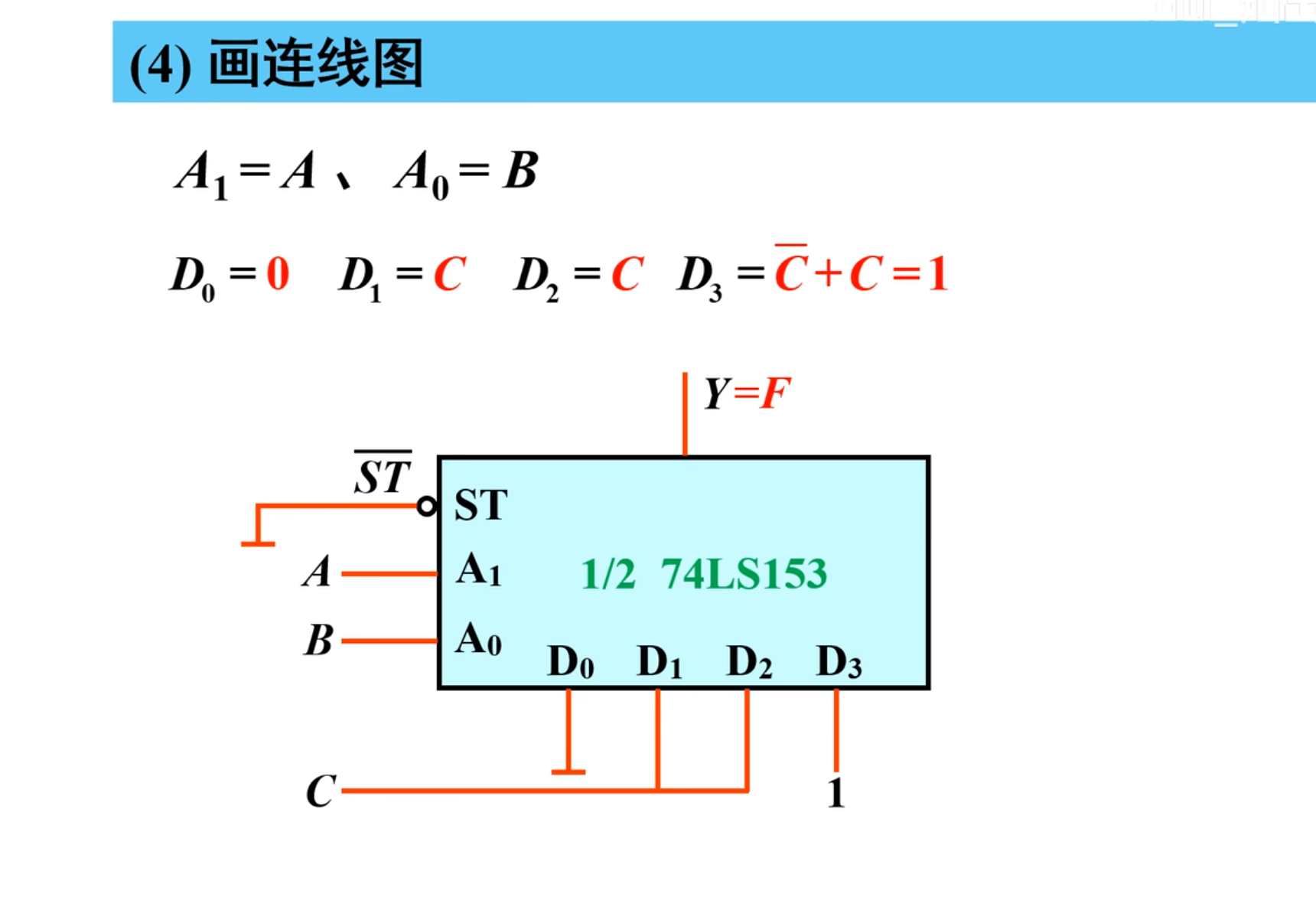
这个方法有一定的局限性，当变量比较多的时候，可能会拼凑错，下面的方法是图形法（卡诺图）

方法：

IMPORTANT

先画出待求函数的降维卡诺图，再画出相应数据选择器输出信号的卡诺图，利用两者相等的关系，求出数据选择器输入变量的表达式

NOTE

一般将卡诺图的变量数称为该图的维数，如果把某些变量也作为卡诺图中小方格的值，则会减少卡诺图的维数，这种卡诺图称为“降维卡诺图”

下面就是降维的具体操作：

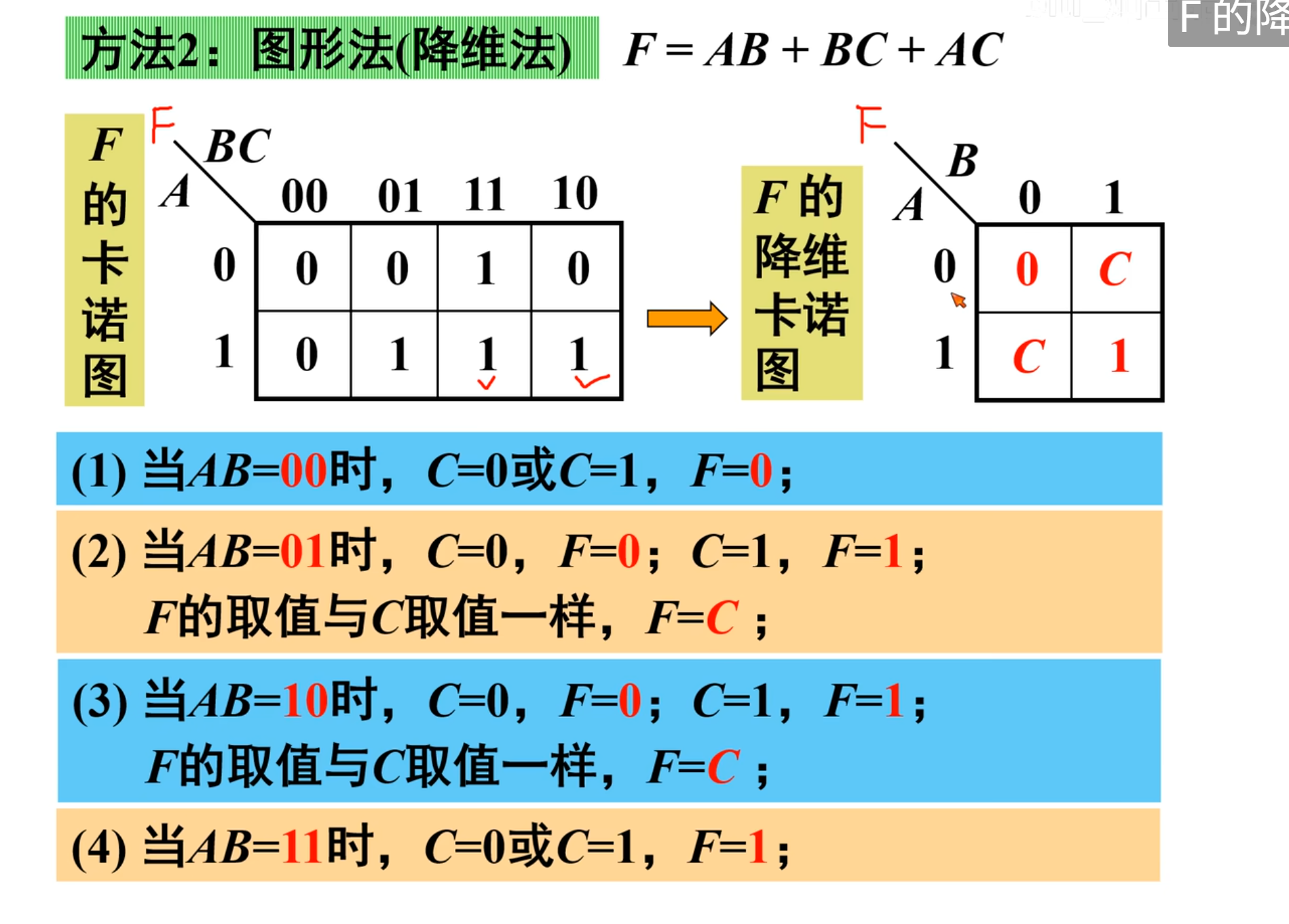
当然，上面包含 $C$ 的是包含的原变量，如果当 $C=0$ ， $F=1$ ， $C=1$ ， $F=0$ 的时候，结果就是 $F=\bar{C}$

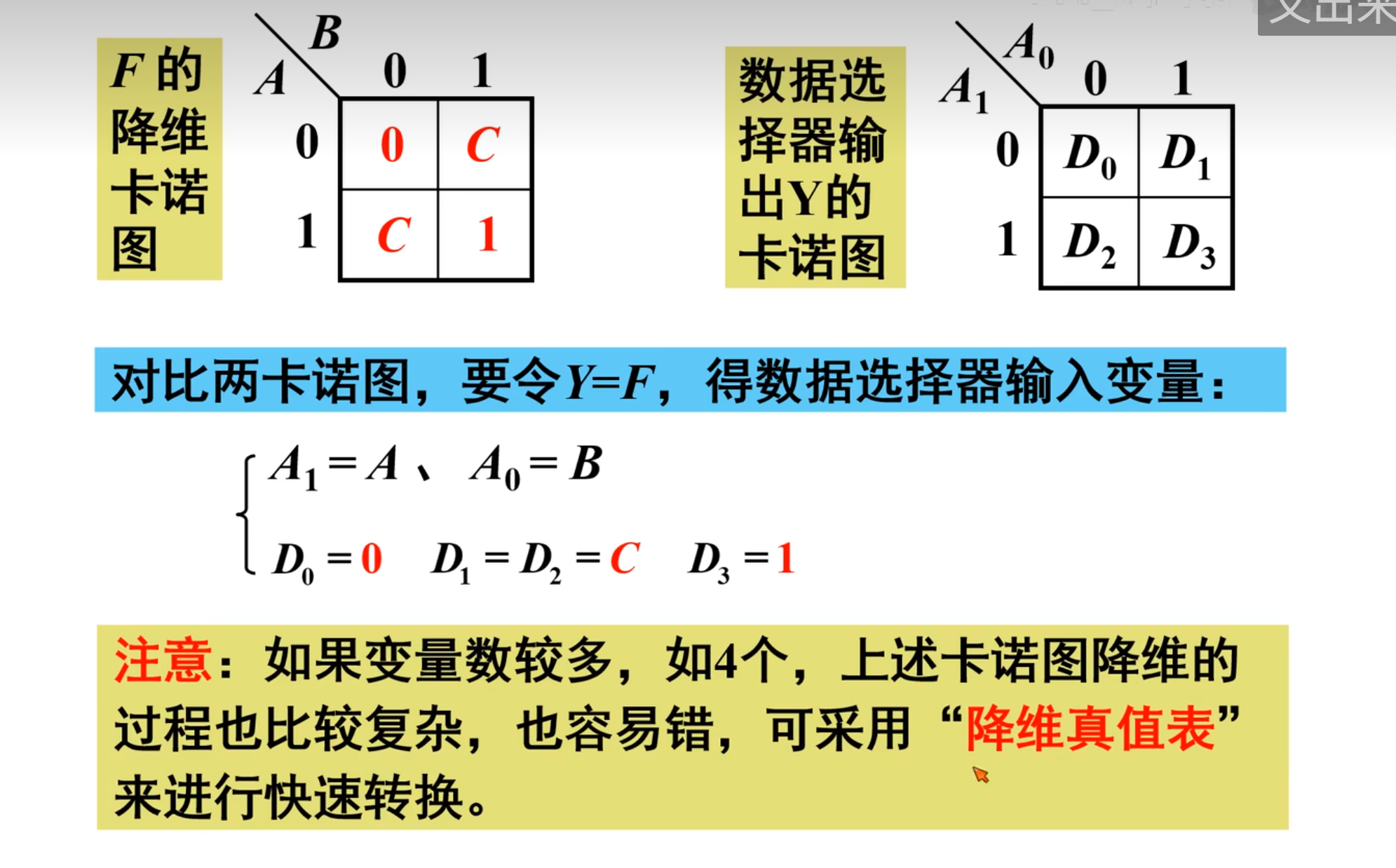
下面就是来对比 $F$ 的降维卡诺图和数据选择器输出 $Y$ 的卡诺图

当然，需要注意的还是 $A=A_1$ ， $B=A_0$ ，高低位对应

除了上面的这种方法，还有更快的方法：

就是“降维真值表”的方法

首先就是先将待求函数转换成最小项之和的形式

$$F=AB+BC+AC=\sum m(3,5,6,7)$$

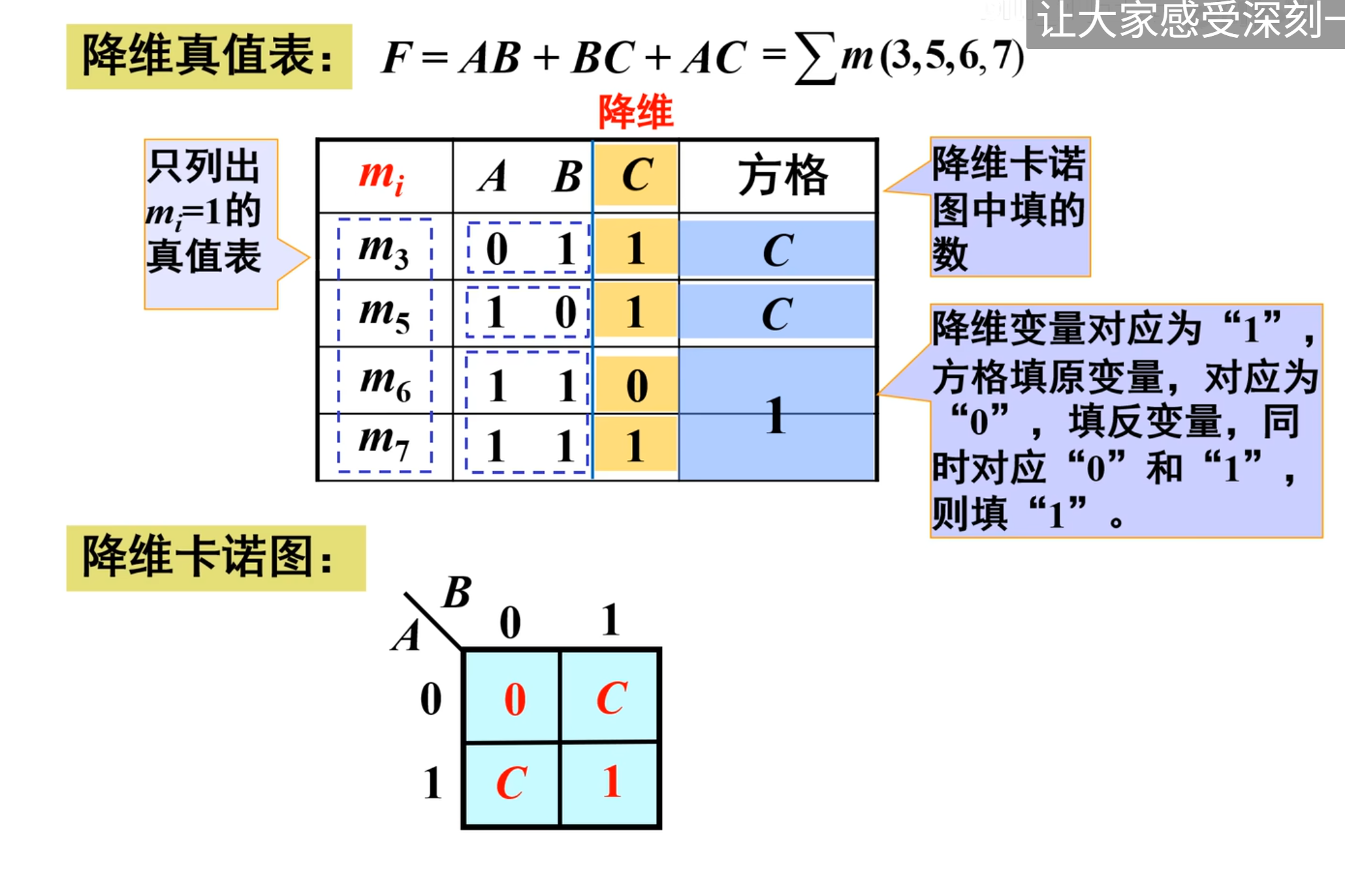
下面开始列表，根据上面图中所示的表一样。

NOTE

如果降维变量在其他变量取值情况唯一的时候 （比如 $A=1、B=0$ 在表中只出现了一次 ），降维变量的取值为 $1$ ，则降维卡诺图中的填降维变量，降维变量的取值为 $0$ ，则填降维变量的反变量

如果降维变量在其他变量取值情况不唯一（不唯一一般为两次）的时候（比如 $A=0、B=1$ 在表中出现了两次 ），降维变量直接为 $1$

NOTE

写出降维真值表之后，紧接着就是画出降维卡诺图，如果降维真值表没有出现卡诺图中相应的取值，则直接写 $0$ ，比如在上面的将为真值表中没有出现 $A=0$ ， $B=0$ 的情况，则在画降维卡诺图的时候对应位置直接写 $0$

NOTE

得到降维卡诺图之后，则是需要将其与数据选择器的卡诺图进行比较，从而得到最后的连线方式

---

下面用一个变量数比较多的情况来展示：

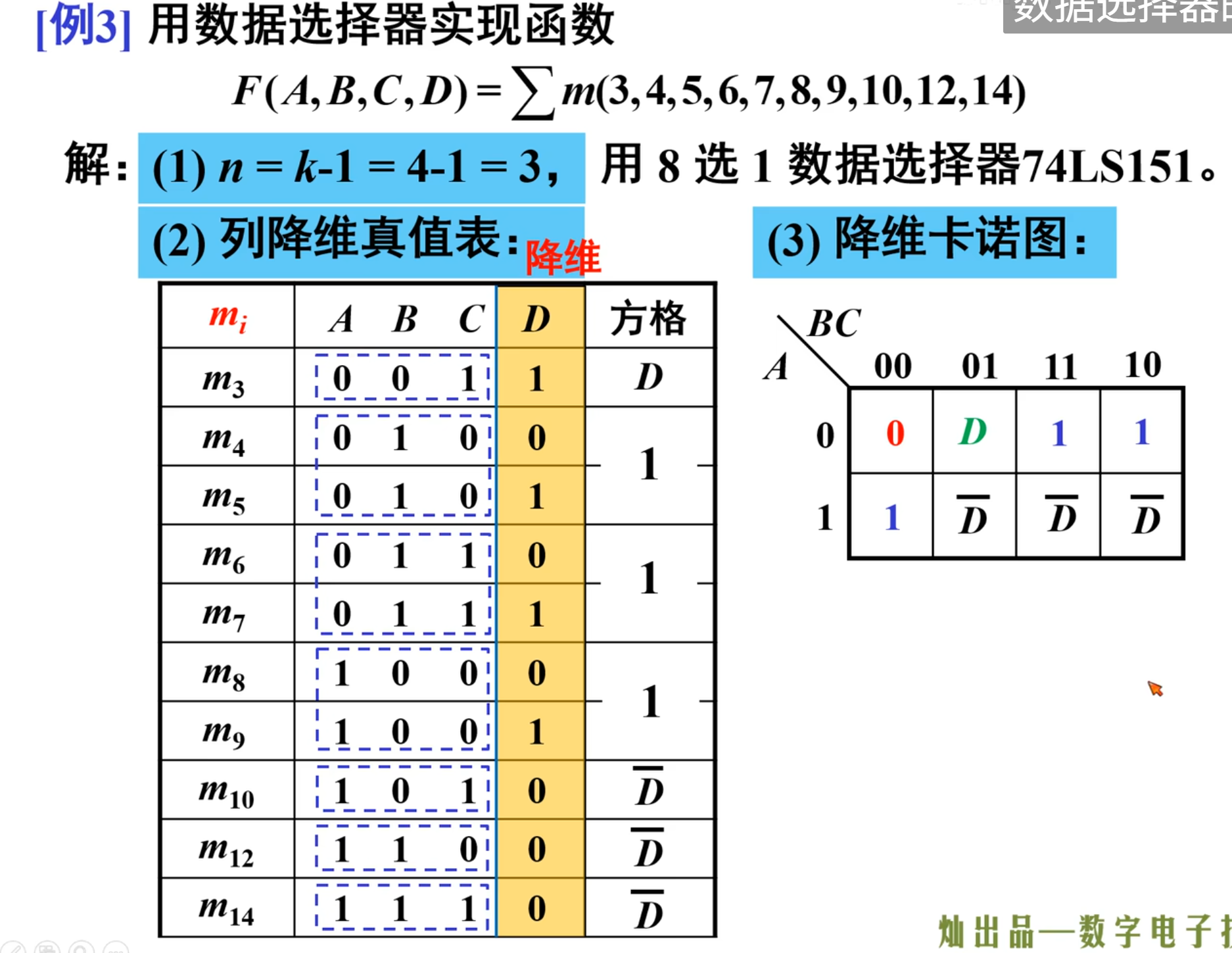
然后是对比 151 的卡诺图

最后就是画出连线图：

贡献者

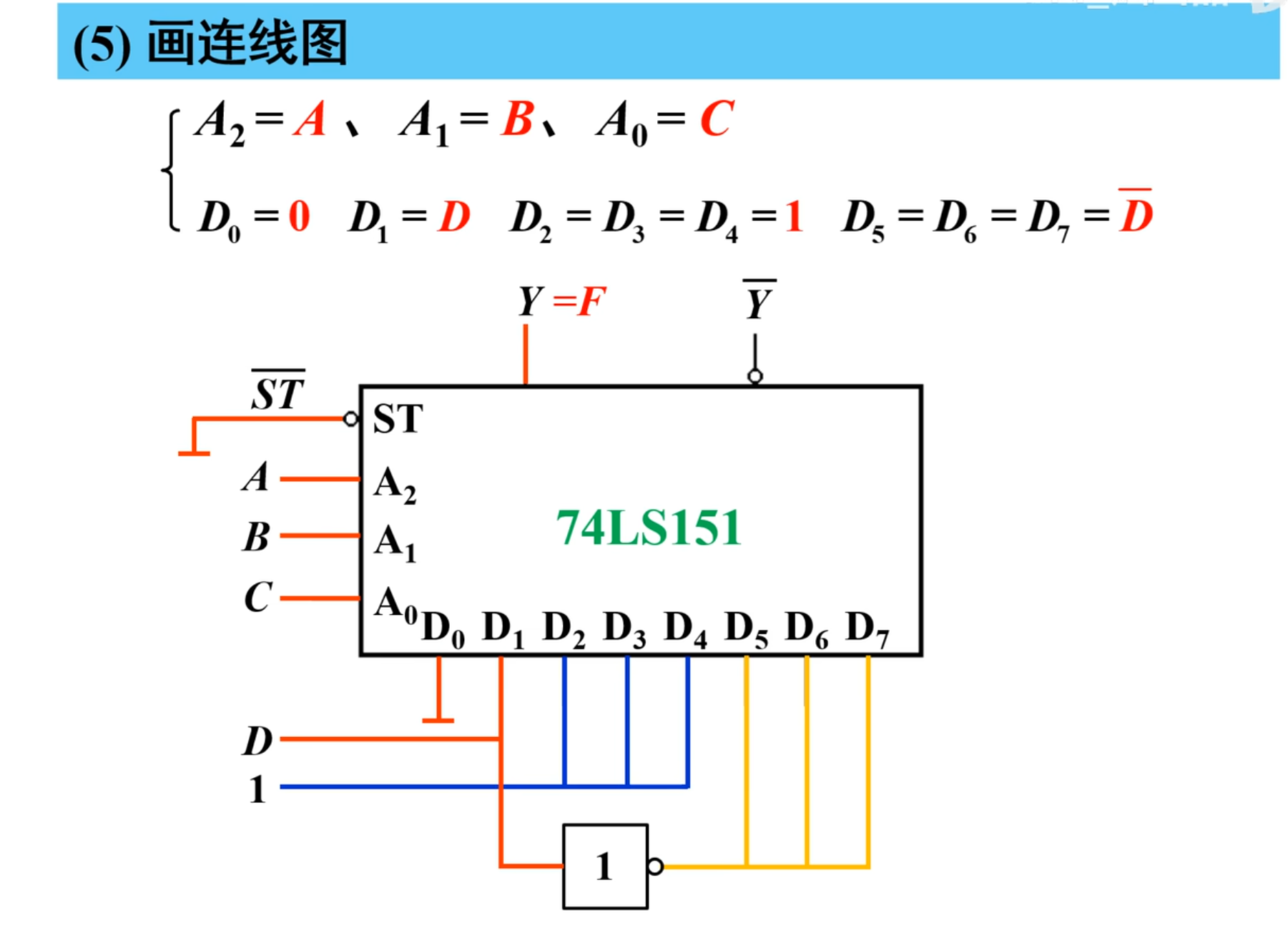
王海平

文件历史

最后编辑于 9 天前查看完整历史

28d3e-笔记上传:2025-10-29 16:54:06