字数

559 字

阅读时间

3 分钟

盖起来算其他（留数法）

IMPORTANT

成立条件：需要满足分子次数小于分母次数，如果得到的结果不能满足这个条件，则需要进行变换，首先是相等的时候：将假分数的分子凑出一个分母来，得到一个 1，然后剩余的部分再使用留数法，其次是分子次数大于分母次数的时候，需要

这部分在高数计算积分的地方，亦有记载

$$\frac{1}{(a+j\omega )(b+j\omega )}=\frac{A}{a+j\omega }+\frac{B}{b+j\omega }$$

求得 $A$ 和 $B$

首先是算什么盖什么

NOTE

盖住的是分式中分母的一部分，然后令这部分等于 0，（这里假设盖住的是 $\frac{A}{(a+j\omega )(b+j\omega )}$ 中的 $(a+j\omega )$ ）计算出 $j\omega =-a$ ，然后把这个 $j\omega$ 代入到被盖住的分式中（去掉被盖住的分母），得到的结果就是被盖住的分式的分子，也就是我们要求的 $A$

同理，计算另外一个没有被盖住的分式的分子就需要盖住另外一个分式。如下图：

下面是这样计算可以得到结果的道理：

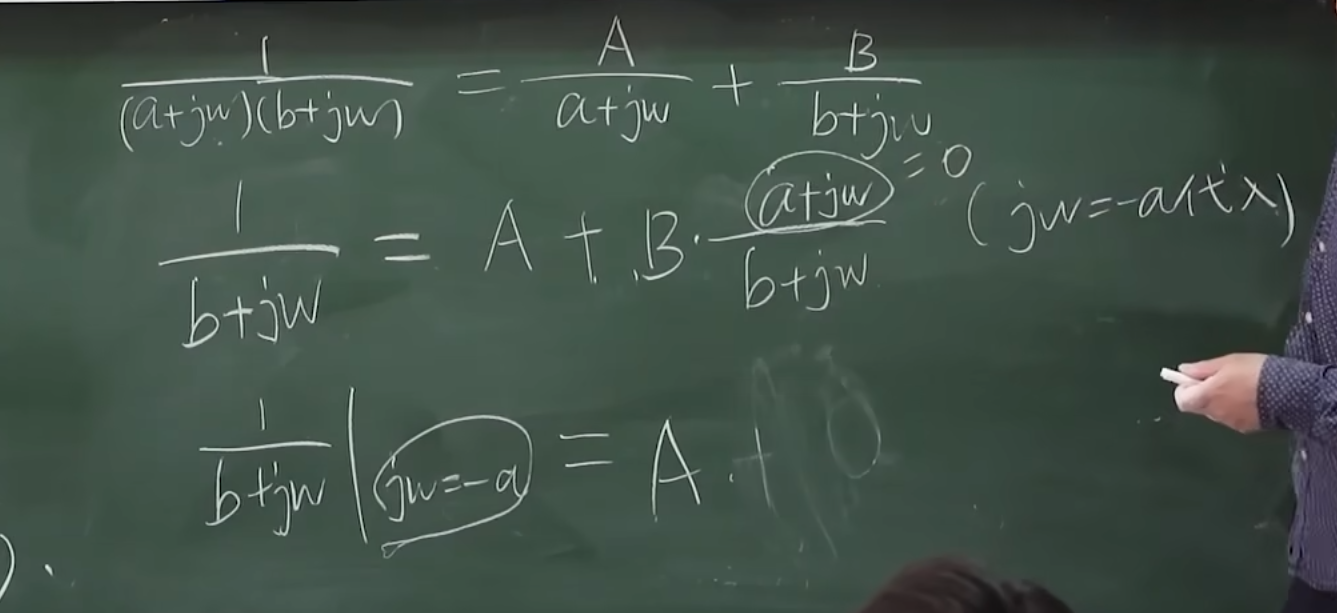
这里需要注意，上面的方法用于分子的最高次幂小于分母的最高次幂。但凡相等就需要降幂处理

然后需要注意的是分子的最高次幂等于分母的最高次幂。

需要的方法是凑出来一个“1”，剩下的部分得到的就是真分式了，然后再使用上面的方法。

最后是分子的最高次幂大于分母的最高次幂。

这个时候需要进行除法计算，将 $j\omega$ 当作是 $x$ ，除法的方法类似于下面：

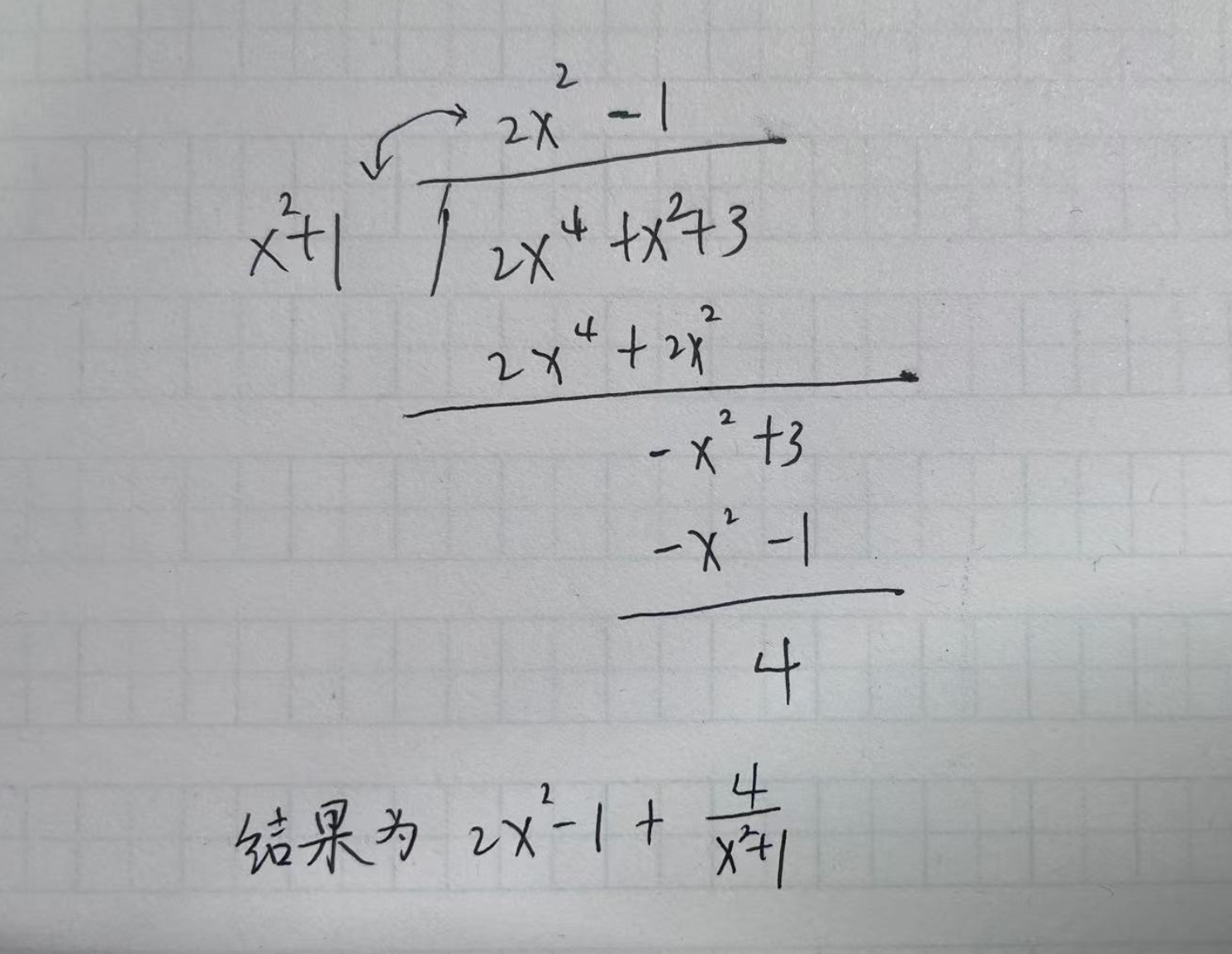
然后再去计算剩下的部分。

这部分在数学笔记的不定积分部分亦有记载。

贡献者

王海平

文件历史

最后编辑于 7 天前查看完整历史

b56b5-笔记上传:2025-10-31 20:46:28

28d3e-笔记上传:2025-10-29 16:54:06