字数

9860 字

阅读时间

40 分钟

数电模电的区别

首先是电子电路分类：

1. 模拟电路
2. 数字电路

模拟信号是在时间上和幅度上都连续变换的信号

数字信号是在时间上和幅度上都断续变化的信号

模拟电路研究的是输出与输入信号之间的大小、相位、失真等方面的关系；

数字电路研究的是输出与输入间的逻辑关系（因果关系）

数字电路中的三极管工作在饱和或者截止状态，起开关作用

描述方法

二值数字逻辑和逻辑电平

逻辑代数

用于描述客观事物逻辑关系的工具。

逻辑体制

正逻辑体制：规定高电平为逻辑 1，低电平为逻辑 0

负逻辑体制：规定高电平为逻辑 0，低电平为逻辑 1

通常，如没有加说明，一般以正逻辑来处理

数制

十进制（Decimal）

不过多描述，就是基本十进制，不过要注意的是下标除了用 $10$ 来表示，还可能用 $D$ 来表示。

数码所处的位置不同，所代表的数值不同。

${10}^i$ 称为十进制的权， $10$ 称为基数， $0\sim 9$ 十个数码称为系数。

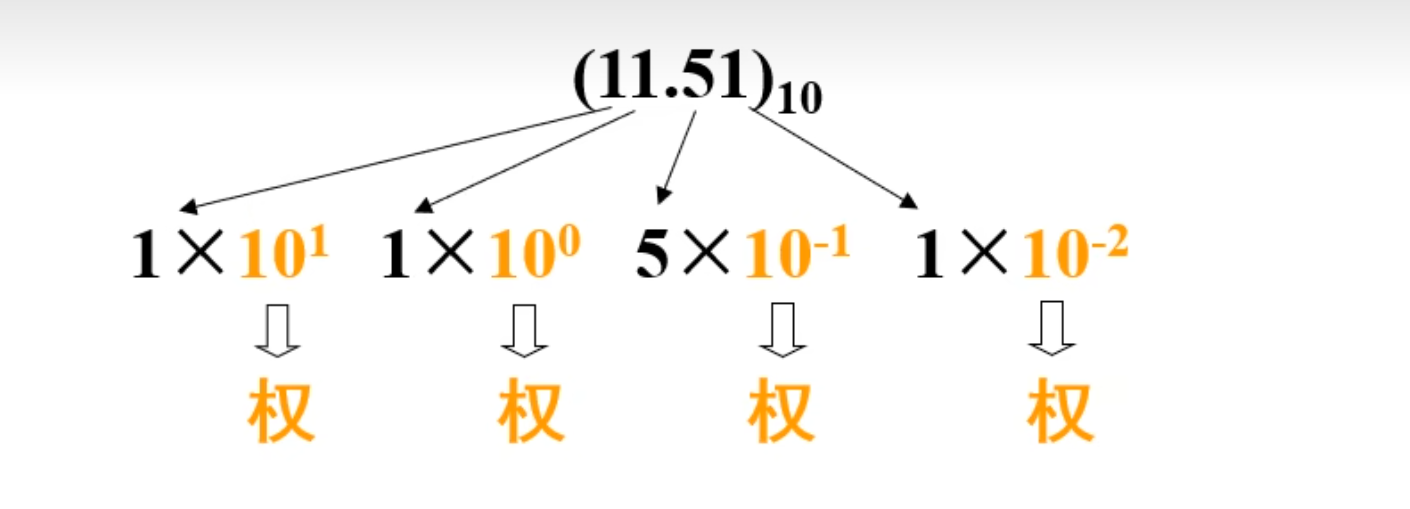
数码与权的乘积，称为加权系数

十进制数可以表示为各位加权系数之和，称为按权展开式

$$(385.64{)}_{10}=3\times {10}^2+8\times {10}^1+5\times {10}^0+6\times {10}^{-1}+4\times {10}^{-2}$$

二进制（Binary）

跟十进制类似，表示方式是右下角标识 $2$ 或者 $B$ ，如： $(1011.11{)}_2$ 、 $(1011.11{)}_B$

二进制的数码： $0$ 、 $1$ ，权： $2^i$ ，基数： $2$

进位规律：逢二进一

将按位权展开式按照十进制规律相加，即得到对应的十进制数，例如：

$$\begin{array}{rl}(1011.11{)}_2& =1\times 2^3+0\times 2^2+1\times 2^1+1\times 2^0+1\times 2^{-1}+1\times 2^{-2}\\ & =8+0+2+1+0.5+0.25\\ & =11.75\end{array}$$

八进制（Octal）

表示方法为 $(XXX{)}_8$ 或者 $(XXX{)}_O$

数码是从 $o\sim 7$ ，权是 $8^i$ ，基数是 $8$

进位规律是逢 8 进 1

将按位权展开相加，即可以得到对应的十进制数

$$(573.46{)}_8=5\times 8^2+7\times 8^1+3\times 8^0+4\times 8^{-1}+6\times 8^{-2}$$

十六进制（Hexadecimal）

$H$ 作为其下标，或者 $16$ 作为其下标。

数码从 $0\sim 9$ ，以及 $A(10),B(11),C(12),D(13),E(14),F(15)$

权是 ${16}^i$ ，基数是 $16$ ，进位规律是逢 16 进 1

这里的加减法不太好算

同样的，这个也可以按位权展开相加，即得到对应的十进制数。

$$(5EC.D4{)}_{16}=5\times {16}^2+14\times {16}^1+12\times {16}^0+13\times {16}^{-1}+4\times {16}^{-2}$$

不同进制之间的相互转换

转换为十进制

主要方法就是按位权展开再求和，上面例子中有说明

十进制到其他进制

NOTE

这部分的方法是：

整数部分采用：除基取余法

小数部分采用：乘基取整法

如何理解，其实不难。

如果是转换成二进制，就将十进制整数部分除以二（短除法），八进制就是整数部分除以八，十六进制就是整数部分除以十六。当然，除完之后，还要取余数。

而小数部分就是成以基数，再取整。

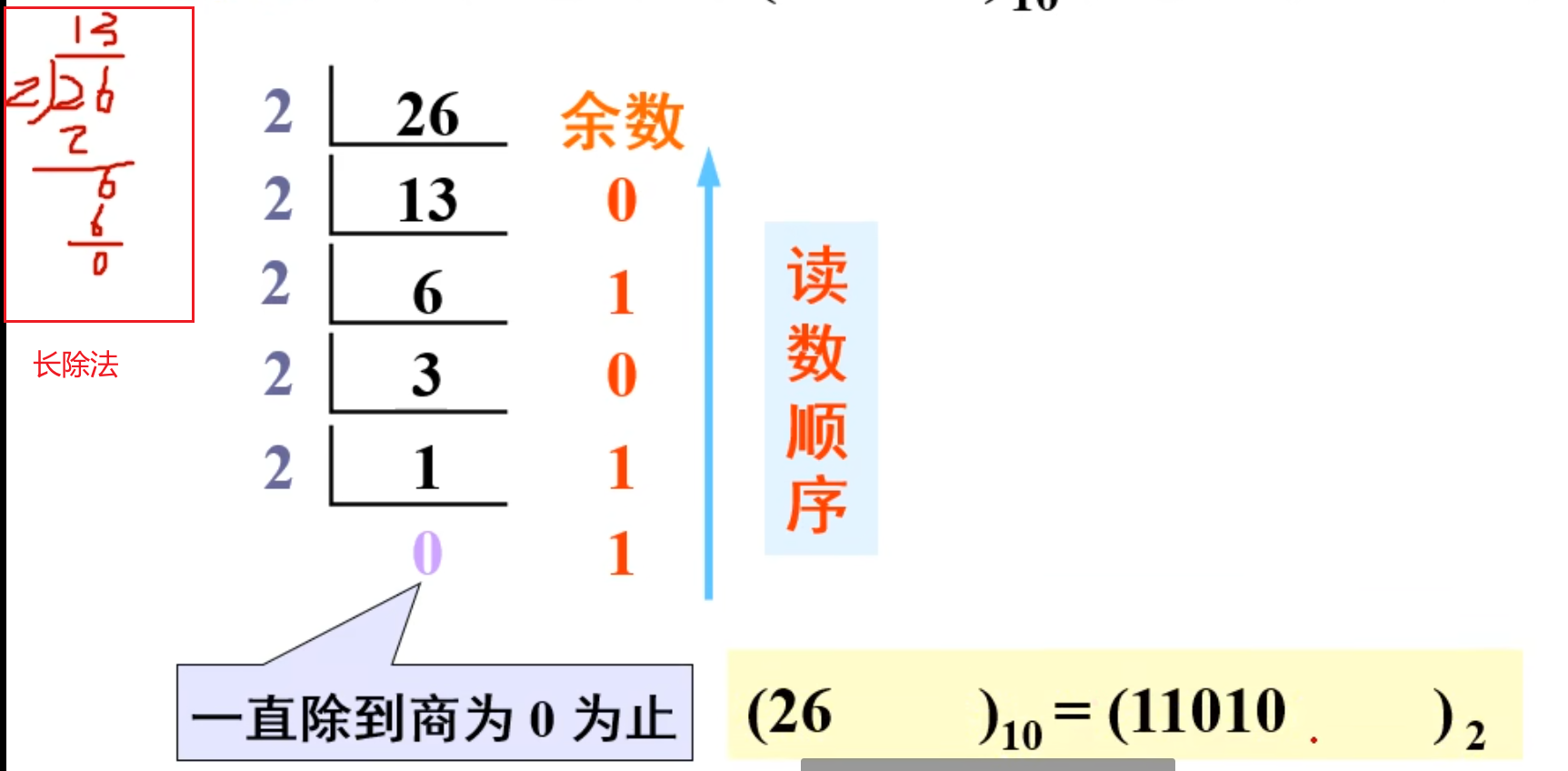
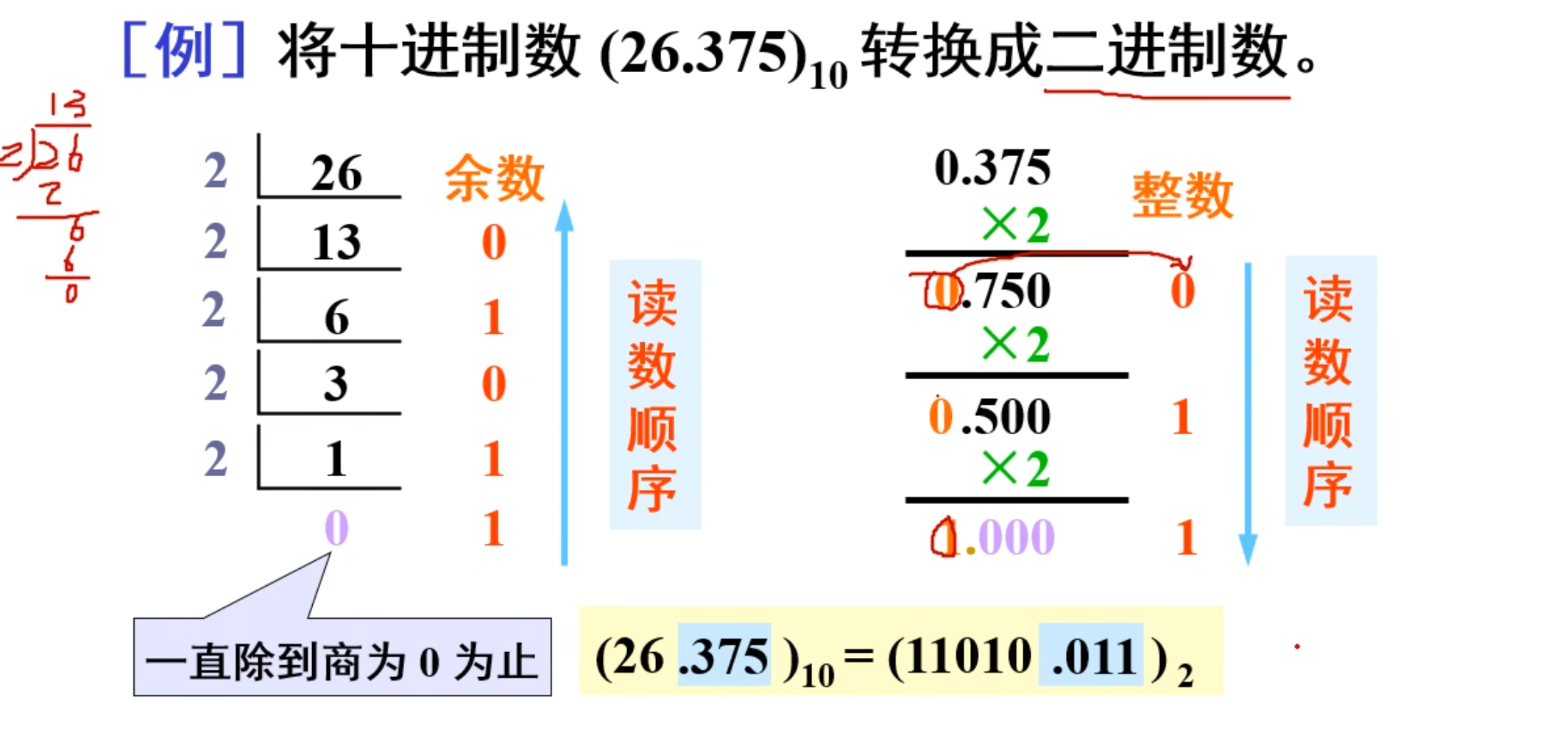
例如：将 $(36.375{)}_{10}$ 转换为二进制。

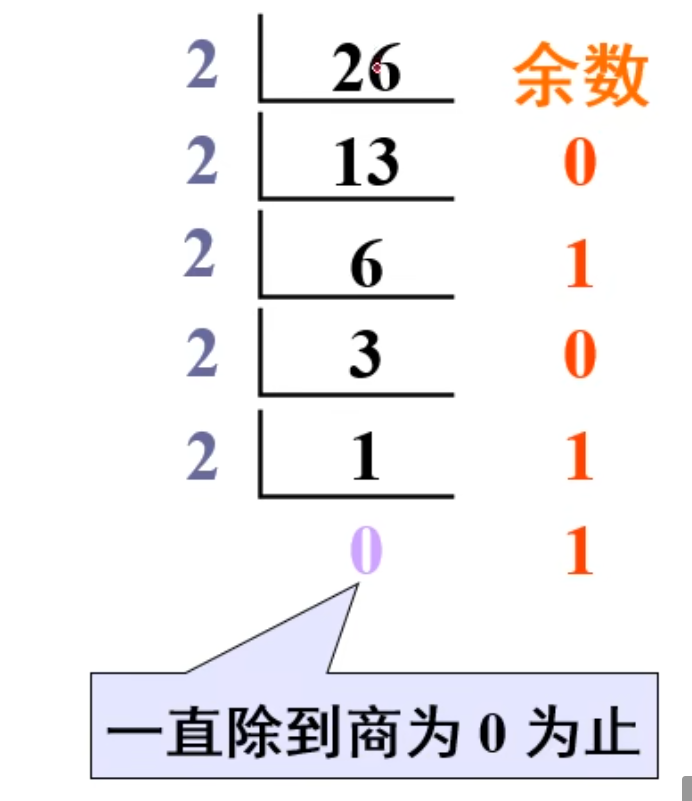
按照上面的除法一直向下除下去，每一次都能得到一个余数，直到商为 0 为止。

而读取的时候，要从下面往上面读。

然后是计算小数部分。

小数部分则是将十进制小数部分的数字拿过来，乘以 $2$ ，然后将得到的整数部分拿过来。注意，无论得到的整数部分是 $0$ 还是 $1$ ，都要拿出来。

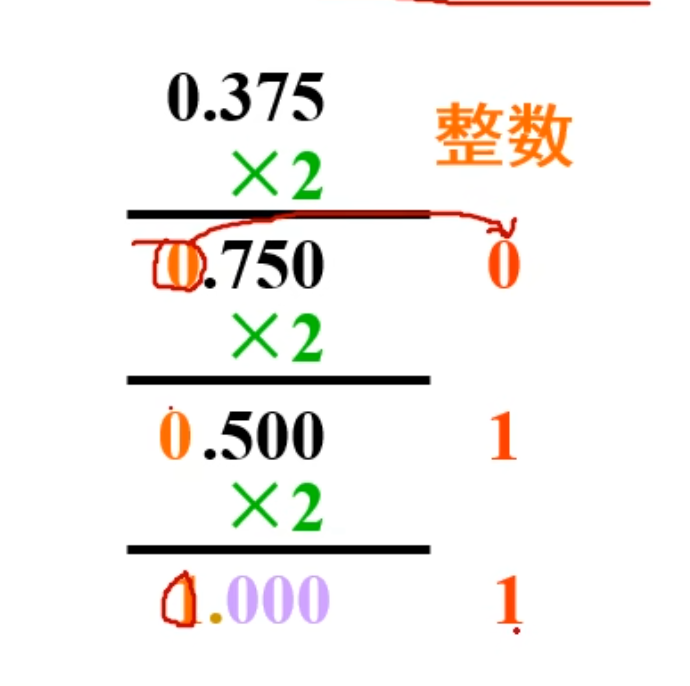
但是，这里有一点需要注意，也是经常会错的地方。

注意看第二次乘以 $2$ ， $0.75\times 2=1.5$ ，这里要把整数部分拿出来。而拿出来之后，剩下的部分再进行乘 $2$ 。 $1.5$ 把 $1$ 拿出来之后就只剩下 $0.5$ 了，所以后面再乘以 2 的部分是 $0.5$

直到最后得到的是 $0$ 乘以 $2$ 。当然，也有可能永远也得不到 $0$ ，那么只需要保留上几位小数即可。（注意看上图中的最后一次乘 $2$ ， $0.5\times 2=1$ ，而这里还是要把 $1$ 拿出来，最后剩下一个 $0$ 才算结束 ）

而读取的顺序则是和整数部分正好相反。

整数部分是从下往上读，而小数部分则是从上往下读。

下面是这个例题：

其他进制也是一样的方法，就是基变了而已。

二进制与八\十六进制快速转换

首先是二进制、八进制和十六进制之间的相互对照表。

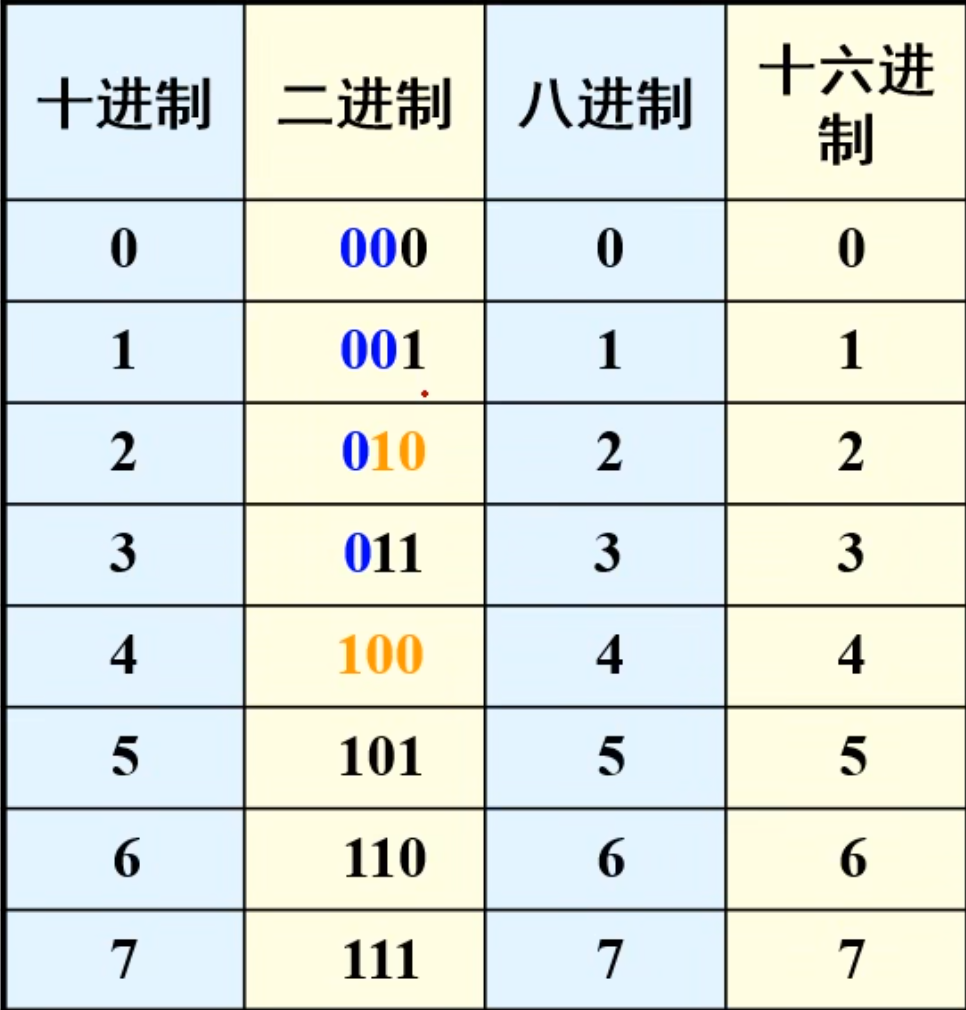
根据相互对照表，可以得到：一位八进制数需要 3 位二进制数来表示

下面是全部的对照：

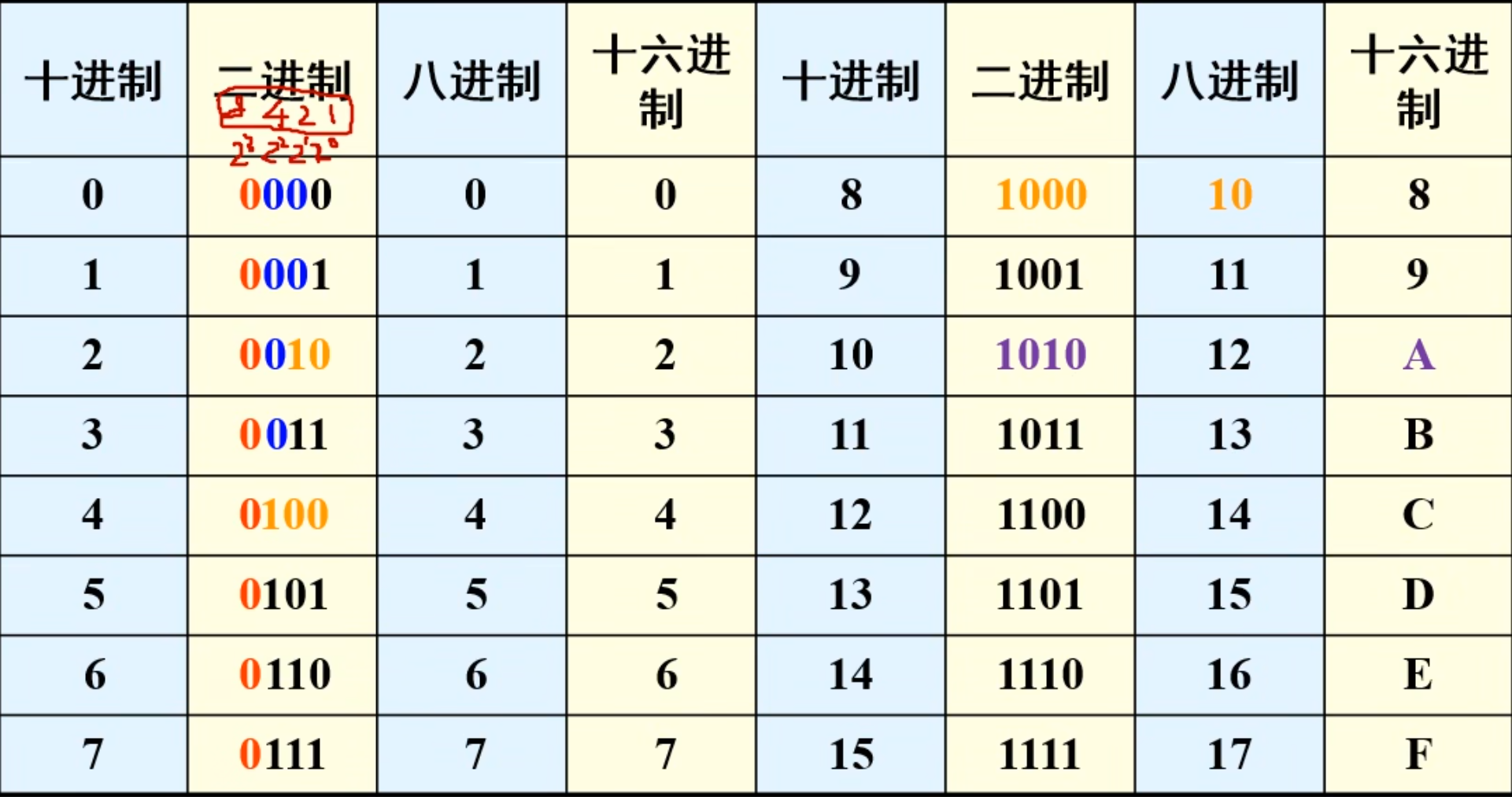
可以得到：1 位十六进制数需要用 4 位二进制数来表示

二进制与八进制

二进制到八进制：

NOTE

从小数点开始，整数部分向左、小数部分向右三位一组，不足三位的加 $0$ 补足（两边）三位，再按照顺序写出各组对应的八进制数

例如：

$$(11100101.11101011{)}_2=({)}_8$$

整数部分和小数部分分别按照上面的方法，三位一组划分开来，得到：

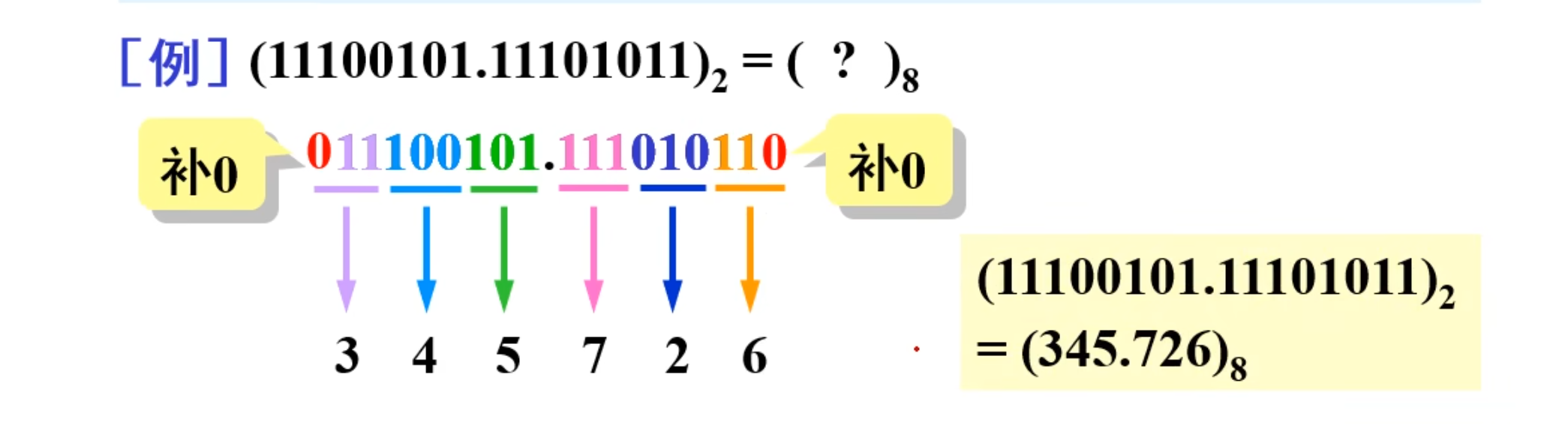
由于是转换到八进制上，所以是三个一组，而根据对应表（421）的方法就可以得到八进制数是多少。

八进制到二进制：

NOTE

将每位八进制数用三位二进制数代替，再按照原来的顺序排序。

例如：

$$(745.361{)}_8=(111100101.011110001{)}_2$$

二进制与十六进制

注意，一位十六进制数对应 4 位二进制数，因此二进制数 4 位为一组。

二进制到十六进制：

NOTE

从小数点开始，整数部分向左、小数部分向右四位一组，不足四位的加 $0$ 补齐四位，再按照顺序写出各组对应的十六进制数。

例如：

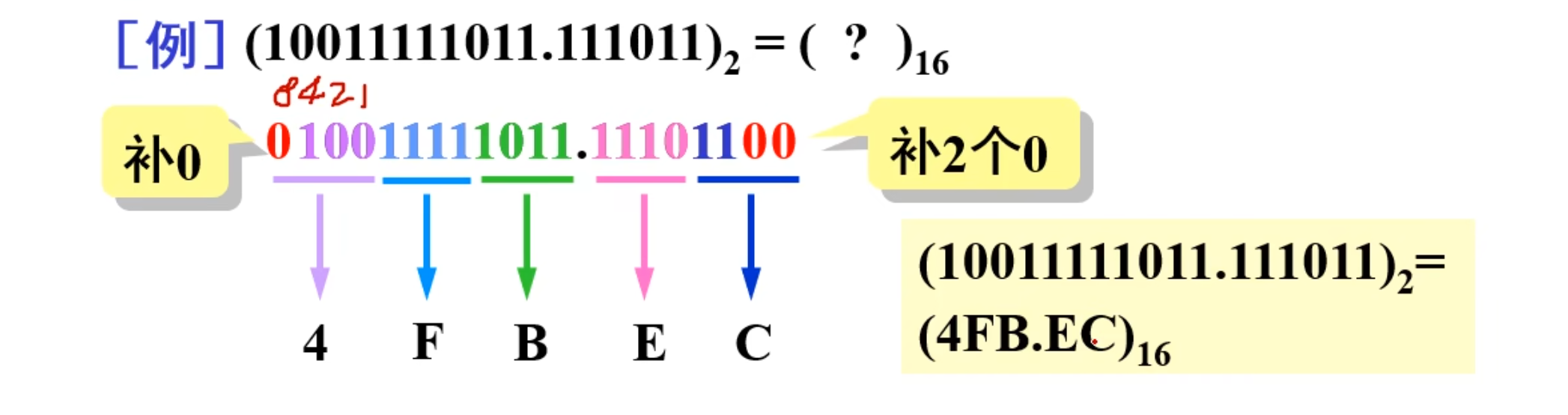
十六进制到二进制：

NOTE

每位十六进制数用四位二进制数代替，再按照原顺序排列

例如：

八进制与十六进制

这两个之间没有快速转换，只能是利用中间桥梁来实现转换。（比如二进制）

例如：

$$(653.12{)}_8=(110101011。001010{)}_2=(1AB.28{)}_{16}$$

码制

二进制代码

用数码的特定组合表示特定信息的过程称为编码

BCD 码（二进制表示十进制）

四位二进制码有十六种组合，表示 $0\sim 9$ 十个数有多种方案，所以 $BCD$ 码有多种

8421 BCD 码

这个是恒权码，取 4 位自然二进制数的前 10 种组合。

这个就是比较常见的哪个 BCD 码

2421 BCD 码和 5421 BCD 码

有权码，从高位到低位的权值分别为 $2、4、2、1$ 和 $5、4、2、1$

余 3 BCD 码

这个是无权码

无权码表示不能用之前 8421 之类的一样的去乘，没有这样的规律。

比 8421 BCD 码多余 3 (0011)

8421 BCD 是从 0000 开始的，而余 3 BCD 码是从 0011 开始的

例题

用 BCD 码来表示十进制数码

$$(36{)}_{10}=(00110110{)}_{8421BCD}$$

IMPORTANT

注意，转换成 8421 BCD 数，每一位都要变换。比如有两位数，那么就是分别对这两位进行变换。

例如下面这个：

$$(10{)}_{10}=(00010000{)}_{8421BCD}$$$$(9{)}_{10}=(1001{)}_{8421BCD}$$$$(4.79{)}_{10}=(0100.01111001{)}_{8421BCD}$$

当然，反过来也是很简单的，比如：

$$(01010000{)}_{8421BCD}=(50{)}_{10}$$

可靠性代码

格雷码

格雷码（Gray 码，又称为循环码）

最次位（最右边一位）以 $0110$ 为循环节一直循环四次

此低位（右边数第二个）以 $00111100$ 为循环节一直循环两次

第三位 （右边数第三个）以 $0000111111110000$ 为循环节

最高位（右边数第四个）以 $0000000011111111$ 为循环节

后面在卡诺图那里会用到，其特点是相邻项之间只有 1 位不同

二进制与格雷码互转

NOTE

总结：

二进制数转格雷码：

这个是第一位不变，格雷码的后面一位等于二进制数中对应的此位数与二进制数中前一位数进行异或

格雷码转二进制数：

依然是第一位不变，从第二位开始，二进制数的后面一位等于对应位置的格雷码与前面一位的二进制数进行异或

首先是二进制转格雷码

从二进制的左边开始，右边一位与左边的一位进行异或，如果不同变成 1，如果相同变成 0；最高位不变

直接上例题：

$$(101110{)}_B\to (111001{)}_G$$

然后是格雷码转二进制代码。

这个稍微比较复杂

方法是：高位不变，后面的低位，由前一高位与二进制数中对应位异或得来。

比如说，要求二进制中的第二高位，则是由二进制中的第一高位与格雷码中的第二高位异或，得到的值就是二进制的第二高位。

直接上例题：

$$(11010{)}_G=(10011)$$

图解：

奇偶校验码

奇偶校验码由两部分组成：

1. 信息码：需要传送的信息本身
2. 1 位校验码：取值为 $0$ 或者为 $1$ ，以使整个代码中 $1$ 的个数为奇数或者偶数

使 " $1$ "的个数为奇数的称为奇校验，使 " $1$ "的个数为偶数的称为偶校验

NOTE

举个例子：如果信息码是 $0110$ ，并且使用 8421 奇校验码，那么还要再加上一个校验码 $1$ ，原因是信息码 $0110$ 中有两个 $1$ ，是偶数，但是使用的是奇校验，所以要再加上一个 $1$ 。反之，如果还是使用奇校验，且信息码是 $1110$ ，那么校验码就是 $0$ ，因为信息码中 $1$ 的个数已经是奇数了，不需要加上一个校验码凑出奇数来了。

基本逻辑运算与复合逻辑运算

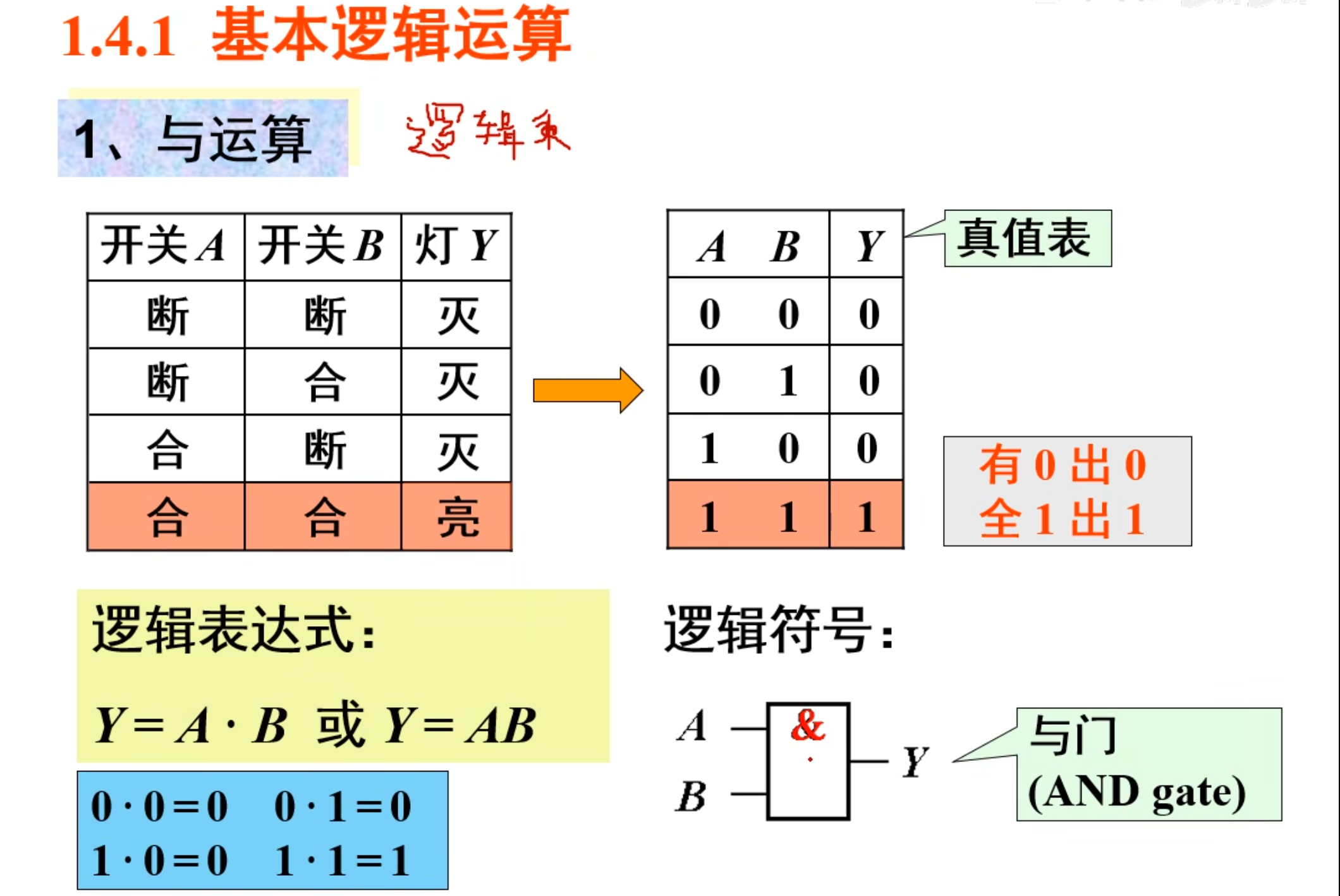
与运算

NOTE

当决定某一件事的所有条件都满足的时候，该事件才会发生。

例子：

记忆：有 0 出 0，全 1 为 1

其逻辑表达式为：

$$Y=A\cdot B=AB$$

当然，还有相对应的电路符号。在下图中。其实就是 c 语言中的 &

或运算

NOTE

当决定某一件事情的诸多条件中，只要有一个或者一个以上的条件具备时，该事件就发生。

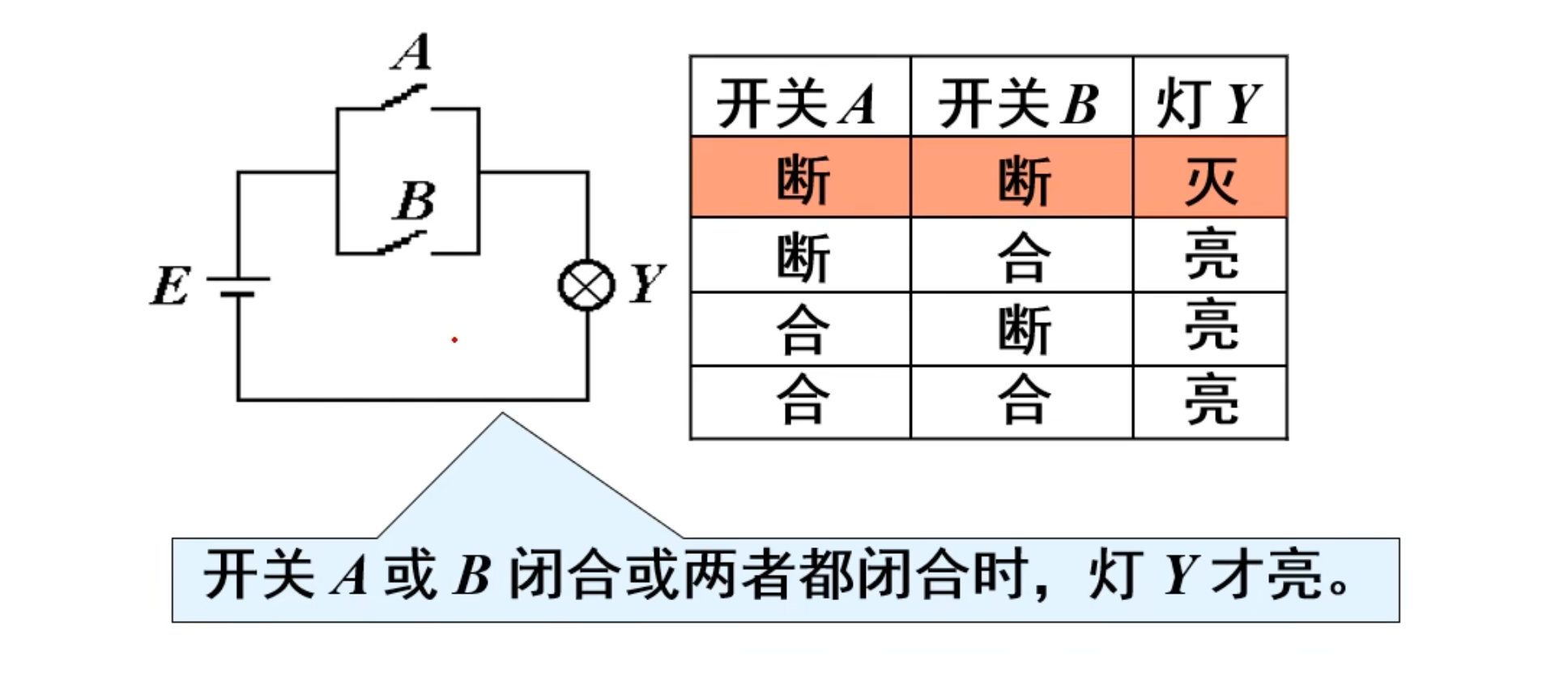
记忆：有 1 出 1，全 0 出 0

逻辑表达式为：

$$Y=A+B$$

电路符号表达在下图中：

非运算

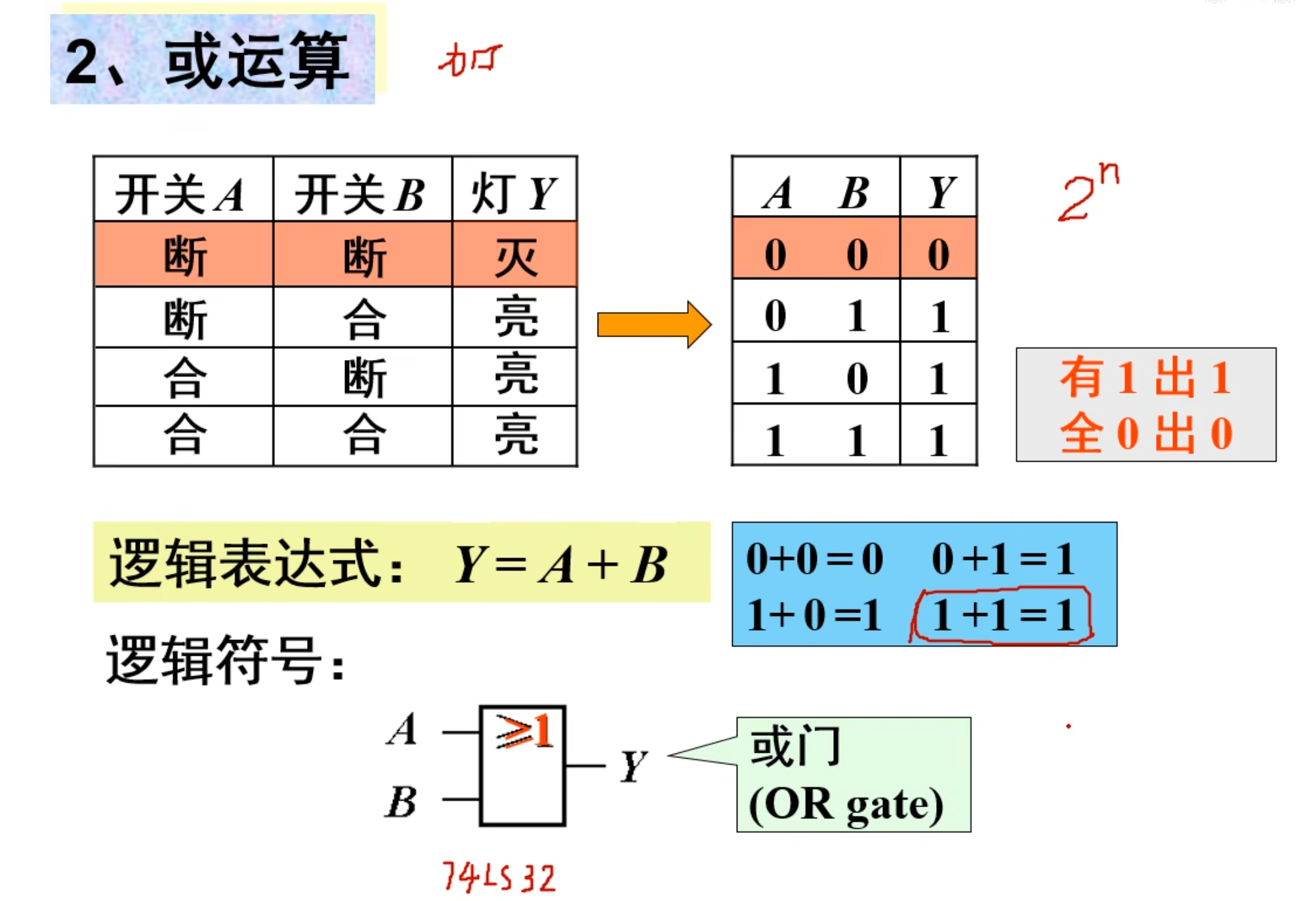
当决定某件事的条件满足时，事件不发生；反之事件发生。

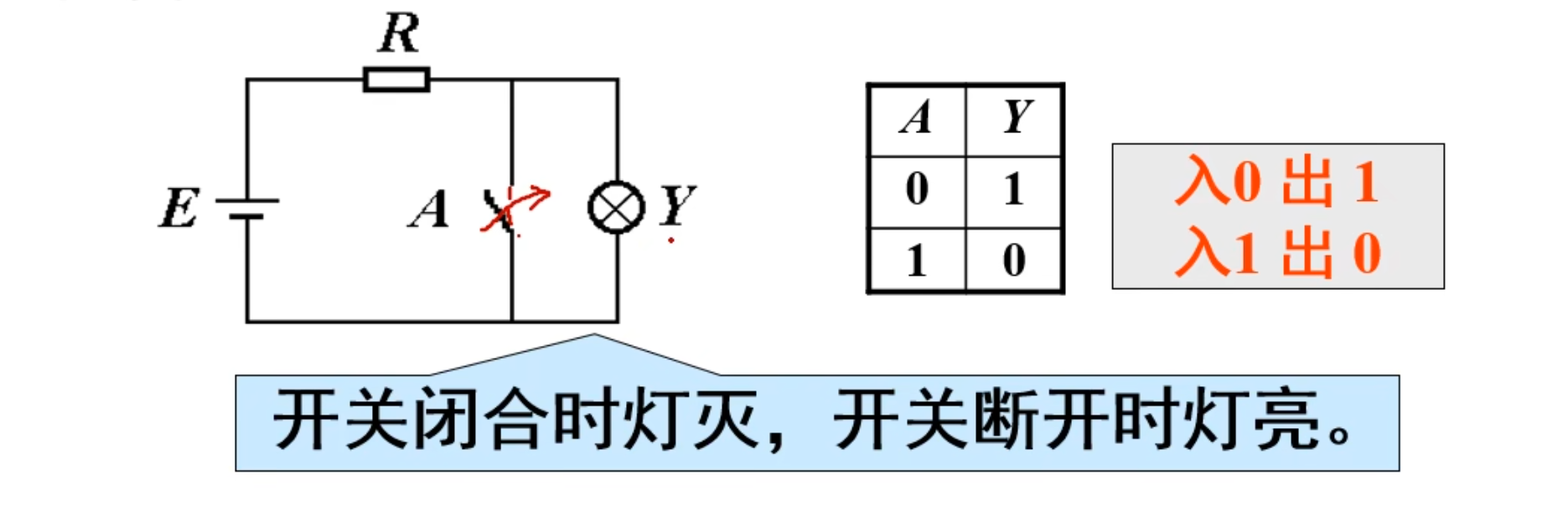
记忆：入 0 出 1，入 1 出 0

逻辑表达式：

$$A=\bar{A}$$

电路符号表达在下图中：

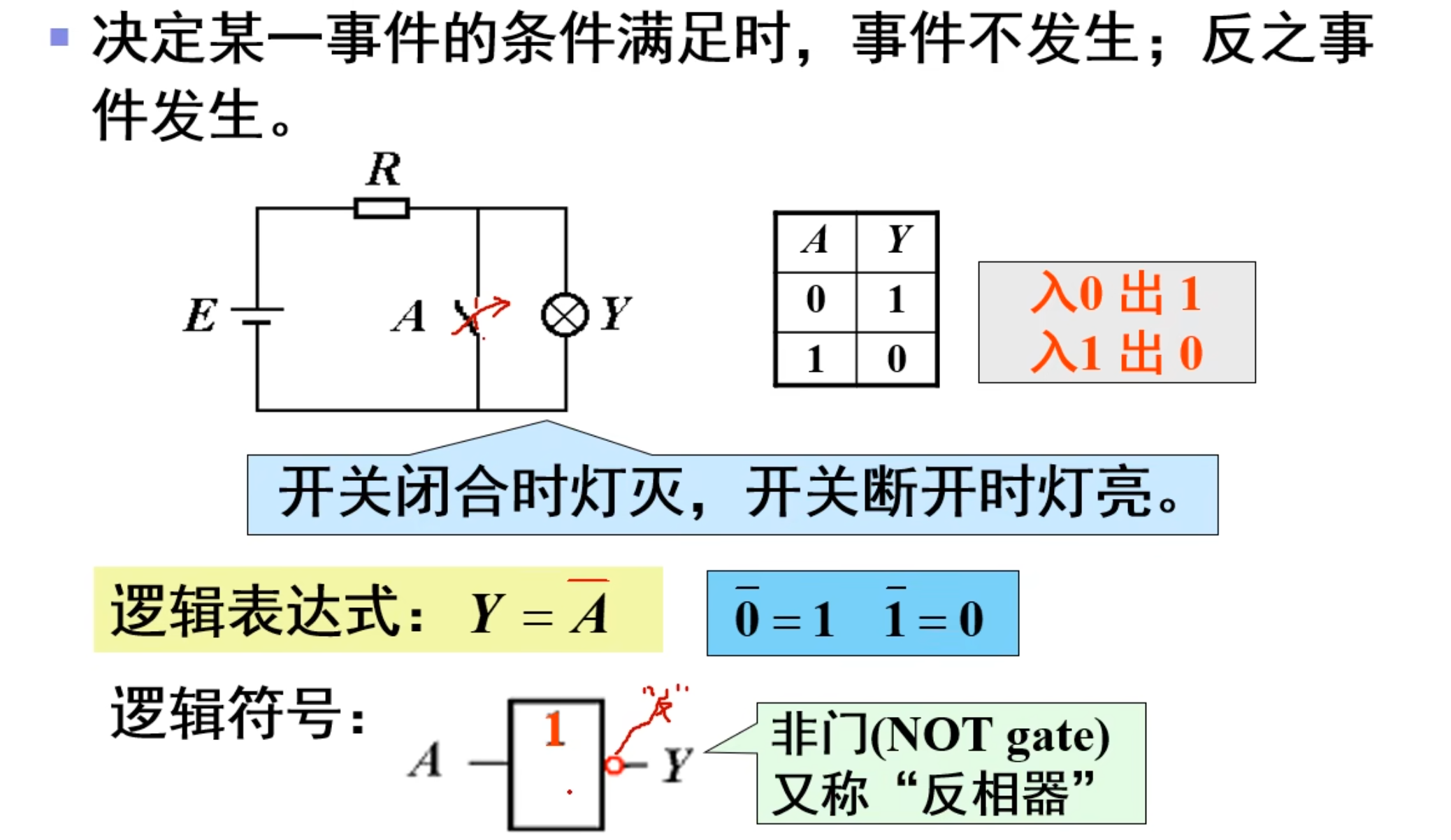
与非运算（NAND）

记忆：有 0 出 1，全 1 出 0

其本质上就是 先与后非

逻辑表达式为：

$$Y=\overline{AB}$$

电路符号表达在下图中

或非运算（NOR）

记忆：有 1 出 0 ，全 0 出 1

其本质上是 先或后非

逻辑表达式为：

$$Y=\overline{A+B}$$

电路符号表达在下图中

异或运算（Exclusive-OR）

记忆：相同为 0，不同为 1

逻辑表达式为：

$$Y=A\oplus B=\bar{A}B+A\bar{B}$$

电路符号表达在下图中：

NOTE

这里需要注意的是，在电子元器件中，异或运算的输入只有两个，所有如果要设计三变量之间的异或运算，需要组合逻辑电路，在后面会学到。

异或器还能组成反相器

$$1\oplus A=\bar{A}$$$$0\oplus A=A$$

同或运算（Exclusive-NOR）

记忆：相同为 1，不同为 0

本质上就是异或运算取非运算得到的。

逻辑表达式：

$$\begin{array}{rl}Y& =A\odot B\\ & =\overline{A\oplus B}\\ & =\bar{A}\bar{B}+AB\end{array}$$

电路符号表达在下图中：

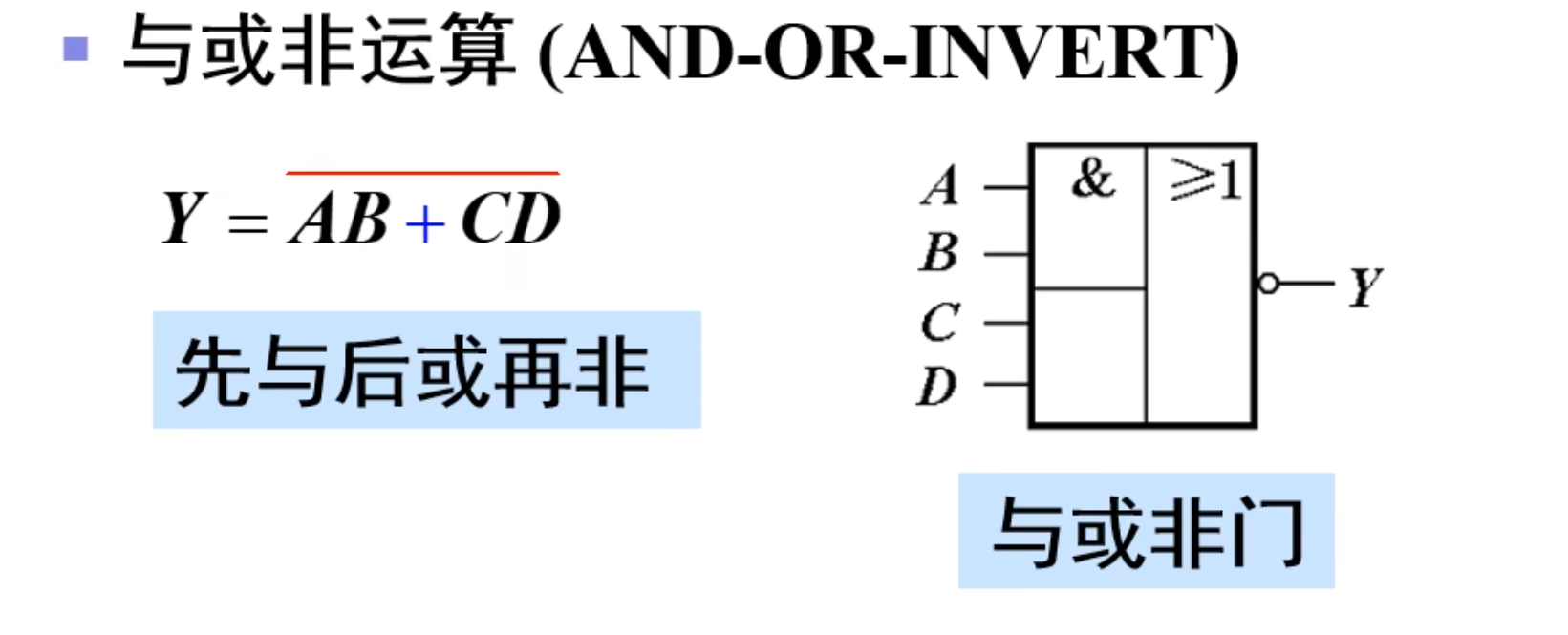
与或非运算（AND-OR-INVERT）

其本质上是先与后或再非

逻辑符号为：

$$Y=\overline{AB+CD}$$

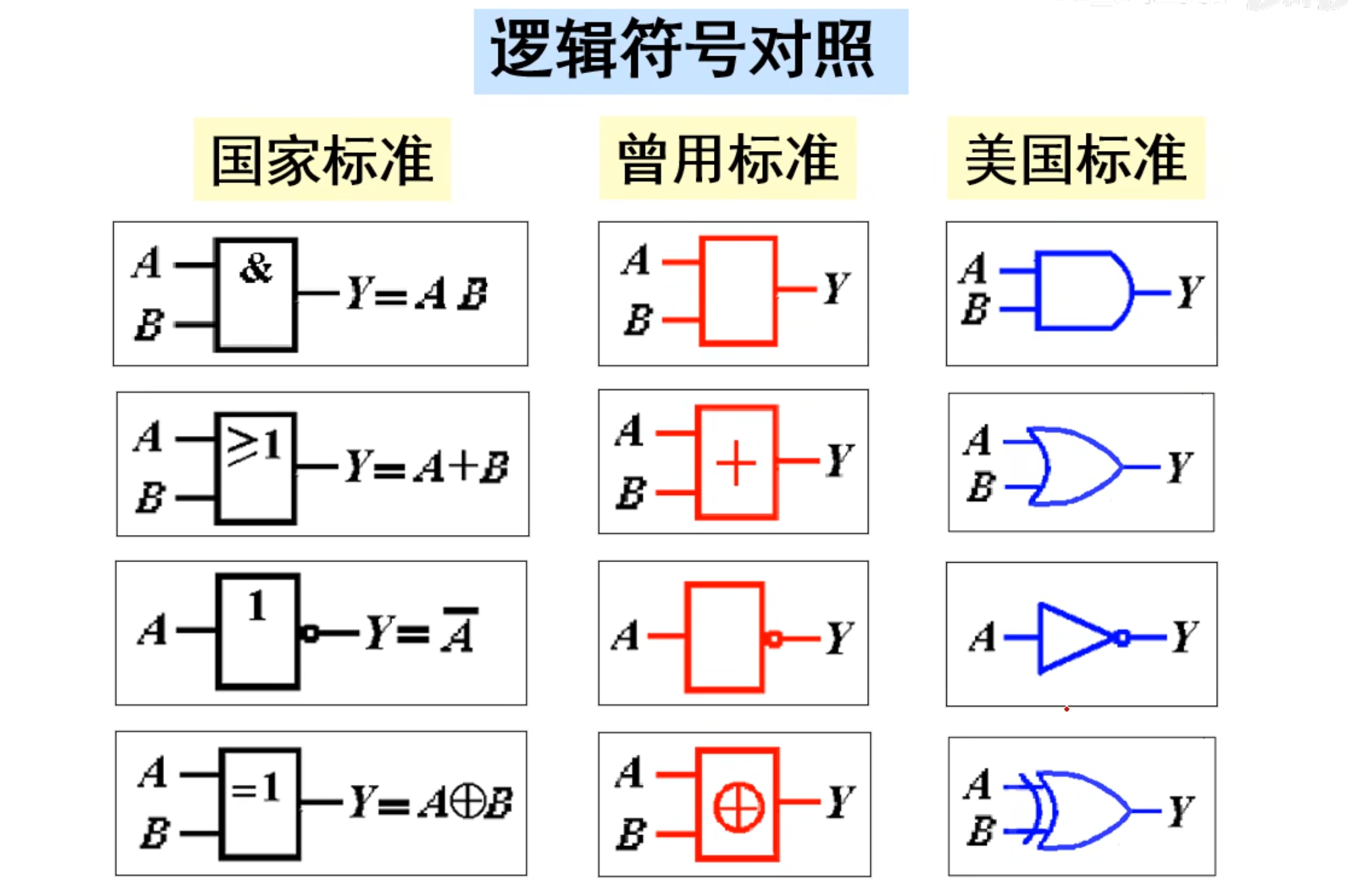
逻辑符号对照

逻辑代数的基本定律与规则

常量之间的运算

与运算、或运算、非运算：

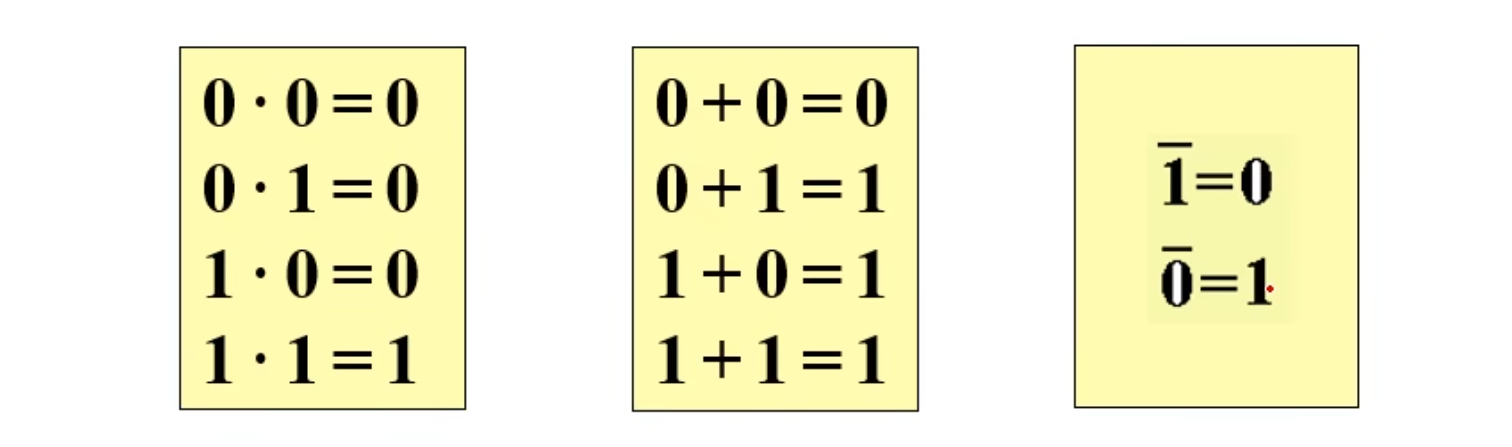
逻辑变量与常量之间的运算

0-1 律

如果之间是与运算，如果与 1 则是本身，与 0 则是 0

如果之间是或运算，如果或 1 则是 1，或 0 则是本身

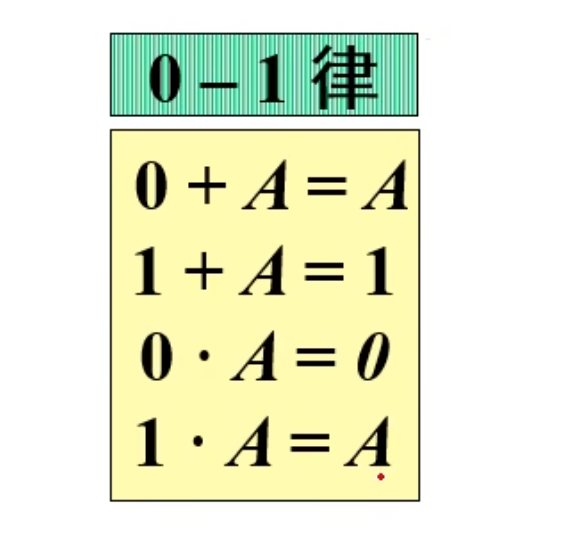
换种记忆方法：

可以将上面的与运算和或运算就当成乘法和加法。（除了 $1+A=A$ ）

NOTE

0 加任何数都是任何数，0 乘任何数都是 0，1 乘任何数都是任何数，当然，1 加 A 是等于 A 的

同一律

这个很好理解：

$$A+A=A$$$$A\cdot A=A$$

将其展开就是 $0\cdot 0=0$ ， $1\cdot 1=1$ ， $0+0=0$ ， $1+1=1$

互补律

$$A+\bar{A}=1$$$$A\cdot \bar{A}=0$$

理解起来也不难，首先是第一个，无论如何，里面肯定有 1，而或运算只要有 1 那就是 1。

第二个，无论如何，里面肯定有 0，而与运算只要有 0 那就是 0。

还原律

$$\overline{\stackrel{―}{A}}=A$$

与普通代数类似的定律

交换律

$A+B=B+A$

$A\cdot B=B\cdot A$

结合律

$(A+B)+C=AB+AC$

$(A\cdot B)\cdot C=A\cdot (B\cdot C)$

分配律

$A(B+C)=AB+AC$

$A+BC=(A+B)(A+C)$$AB+C=(A+C)(B+C)$

特别需要注意的是第二个，要把后面与的部分拆开。

IMPORTANT

注意，这里一定要拆开计算，合起来计算是计算错误的。不能直接先计算 $AB$ 再进行或运算

摩根定律（反演律）

$$\overline{(A\cdot B)}=\bar{A}+\bar{B}$$$$\overline{A+B}=\bar{A}\cdot \bar{B}$$

NOTE

这里的定律一定要记住，这个在后面化简公式的时候经常用

推广公式：

$$\overline{A\cdot B\cdot C\cdots }=\bar{A}+\bar{B}+\bar{C}+\cdots$$$$\overline{A+B+C\cdots }=\bar{A}\cdot \bar{B}\cdot \bar{C}\cdots$$

如何正面两个公式相等呢？

第一种方法就是列真值表来对比：

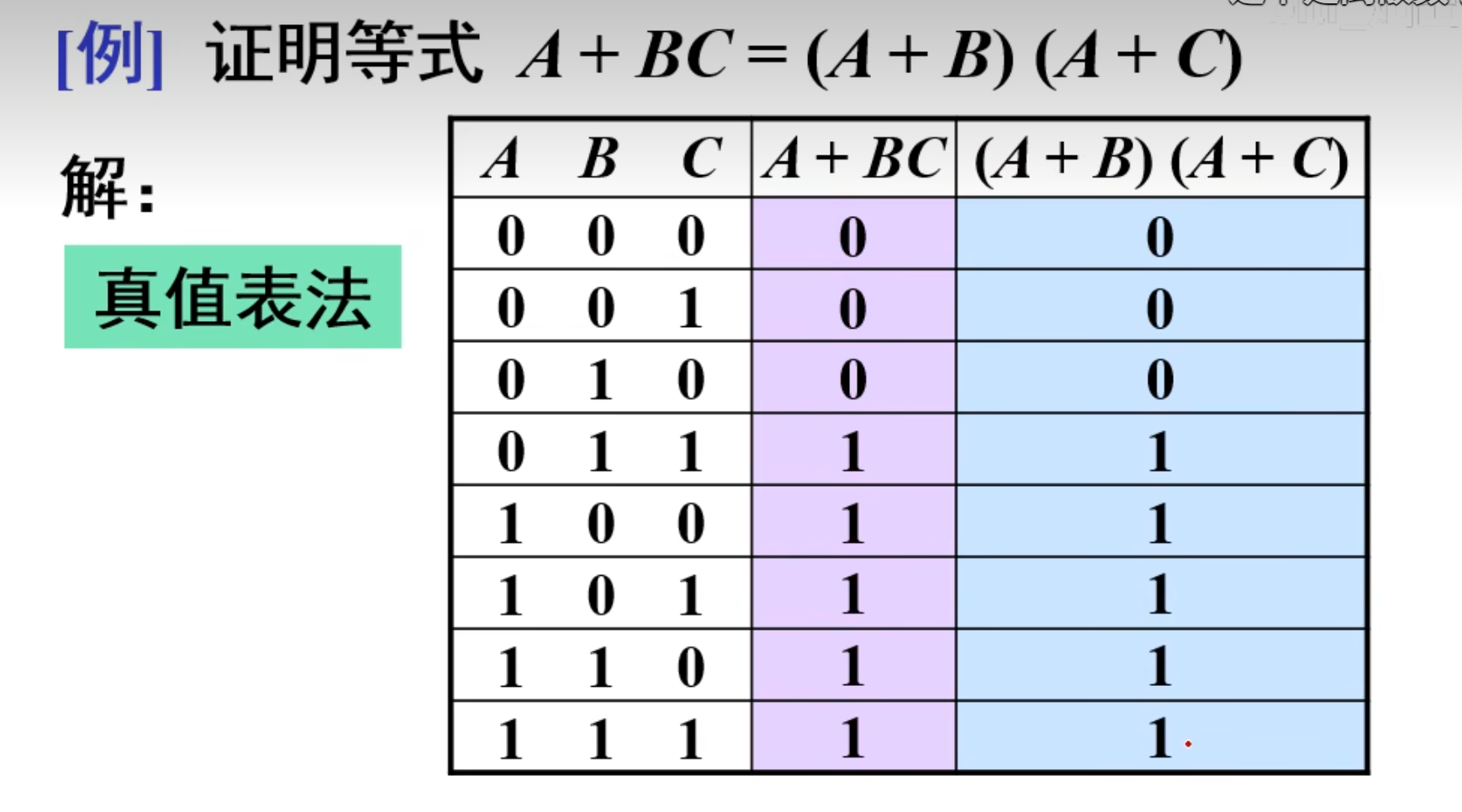
第二种就是公式法：

$$\begin{array}{rl}(A+B)(A+C)& =AA+AC+BA+BC\\ & =A+AC+AB+BC\\ & =A(1+C+B)+BC\\ & =A+BC\end{array}$$

逻辑代数的常用公式

吸收律

一、

$$AB+A\bar{B}=A$$

解释： $AB+A\bar{B}=A(B+\bar{B})=A$

二、

$$A+AB=A$$

解释： $A+AB=A(1+B)=A$

三、

$$A+\bar{A}B=A+B$$

解释：（用的分配律） $A+\bar{A}B=(A+\bar{A})(A+B)=A+B$

记忆的时候，如果出现一个变量与它的反变量，则直接划去这个反变量就是最后的结果。

推广公式： $\bar{A}+AB=\bar{A}+B$

冗余律

$$AB+\bar{A}C+BC=AB+\bar{A}C$$

这个需要记住的是如何找到冗余项，首先找到主变量，就是 $A$ ，其特点是式子中存在其相反变量 $\bar{A}$ ，那么主变量和主变量取反与的这两项合起来就是冗余项

下面是证明：

$$\begin{array}{rl}AB+\bar{A}C+BC& =AB+AC+BC(A+\bar{A})\\ & =AB+\bar{A}C+ABC+\bar{A}BC\\ & =AB(1+C)+\bar{A}C(1+B)\\ & =AB+\bar{A}C\end{array}$$

推广公式：

$$AB+\bar{A}C+BCD\cdots =AB+\bar{A}C$$

证明：

$$\begin{array}{rl}AB+\bar{A}C+BCD\cdots & =AB+\bar{A}C+BC+BCD\cdots \\ & =AB+\bar{A}C+BC(1+D\cdots )\\ & =AB+\bar{A}C+BC\\ & =AB+\bar{A}C\end{array}$$

上面这个其实是原公式中的右边展开了。

$\overline{A\stackrel{―}{B}+\stackrel{―}{A}B}=\bar{A}\bar{B}+AB$

证明其实也不难：

$$\begin{array}{rl}\overline{A\stackrel{―}{B}+\stackrel{―}{A}B}=\overline{A\stackrel{―}{B}}\cdot \overline{\stackrel{―}{A}B}& =(\bar{A}+B)(A+\bar{B})\\ & =\bar{A}A+\bar{A}\bar{B}+AB+B\bar{B}\\ & =\bar{A}\cdot \bar{B}+AB\end{array}$$

其本质是

$$\overline{A\stackrel{―}{B}+\stackrel{―}{A}B}=\overline{A\oplus B}=A\odot B=\bar{A}\bar{B}+AB$$

下面来一个推广公式：

$$\overline{AB+\stackrel{―}{A}C}=A\bar{B}+\bar{A}\bar{C}$$

上面这个推广公式比较重要，可以记下来

NOTE

思考：

若已知 $A+B=A+C$ ，则 $B\ne C$

若已知 $AB=AC$ ，则 $B\ne C$

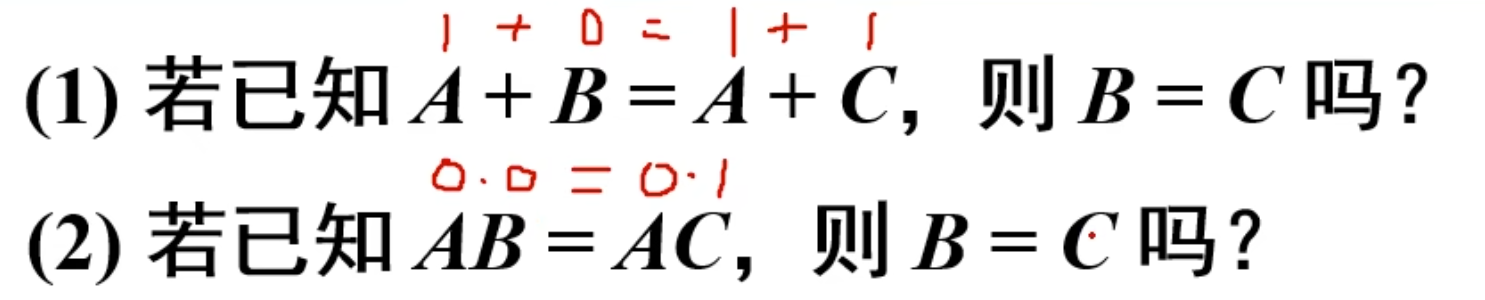
关于异或运算的一些公式

交换律：

$$A\oplus B=B\oplus A$$

结合律：

$$(A\oplus B)\oplus C=A\oplus (B\oplus C)$$

分配律：

$$A\cdot (B\oplus C)=AB\oplus AC$$

常量和变量的异或运算：

$$A\oplus \mathbf{1}=\bar{A}A\oplus \mathbf{0}=AA\oplus A=\mathbf{0}A\oplus \bar{A}=\mathbf{1}$$

异或：相同为 0，不同为 1

同或：相同为 1，不同为 0

因果互换律：

如果 $A\oplus B=C$ 则有 $\{\begin{array}{rl}A\oplus C& =\mathit{B}\\ \mathit{B}\oplus \mathit{C}& =\mathit{A}\end{array}$

逻辑代数的基本规则

代入规则

将逻辑等式两边的某一变量均用同一个逻辑函数替代，等式仍然成立。

例如：

$$A+\bar{A}B=A+B$$

将 $A$ 均用 $\bar{A}$ 来代替，则得到： $\bar{A}+AB=\bar{A}+B$

亦或者，将 $B$ 均用 $C$ 来代替，则得到： $A+\bar{A}C=A+C$

再来一个例子：

$$\overline{A+B}=\bar{A}\cdot \bar{B}$$

将上面公式中的 $B$ 交均用 $B+C$ 来代替，则得到： $\overline{A+B+C}=\bar{A}\cdot \overline{B+C}$

NOTE

利用代入规则，可以扩展基本定理的应用

反演律

对任一个逻辑函数式 $Y$ ，将式中所有的 “.”换成“+”，“+”换成“.”，“0”换成“1”，“1”换成“0”,，原变量换成反变量，反变量换成原变量，则得到原逻辑函数的反函数 $\bar{Y}$ 。

IMPORTANT

注意：

变换的时候不能改变其运算顺序

原变量变成反变量，反变量换成原变量只对单个变量有效，而对长非号保持不变。

例题：

$$Y_1=A\cdot \overline{B+C}+CD$$

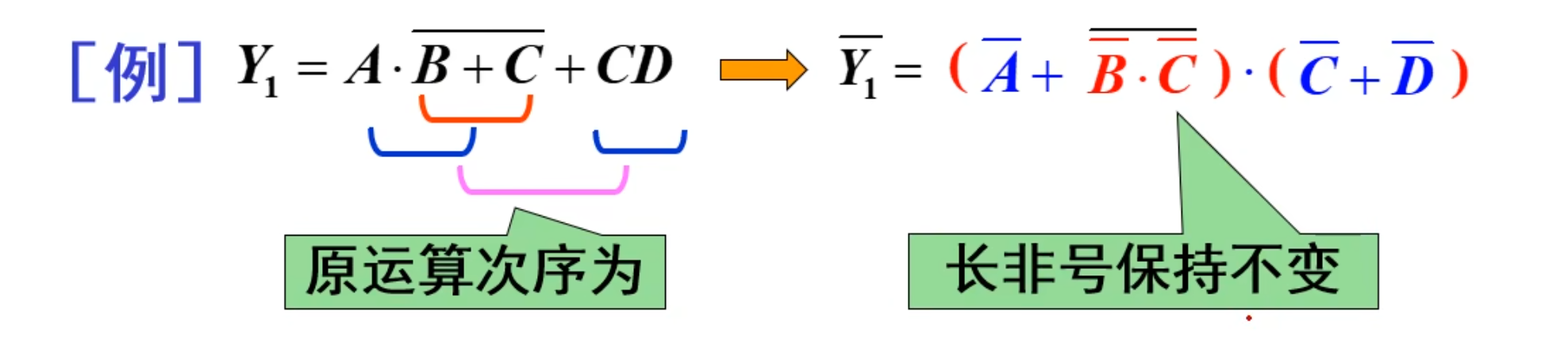
另外一个例题：

$$Y_2=\overline{\stackrel{―}{A\stackrel{―}{B}+C}+D}+E$$

NOTE

求逻辑函数的反函数有两种方法：利用反演规则或者摩根定律来求解。

对偶规则

对任一个逻辑函数式 $Y$ , 将式中所有的“.”换成“+”，“+”换成“.”，“0”换成“1”，“1”换成“0”，则得到原逻辑函数的对偶式 $Y^{\prime }$ 。

IMPORTANT

变换时需要注意的是：

不能改变原来的运算顺序

变量上的非号均不改变

主要作用是定律扩展

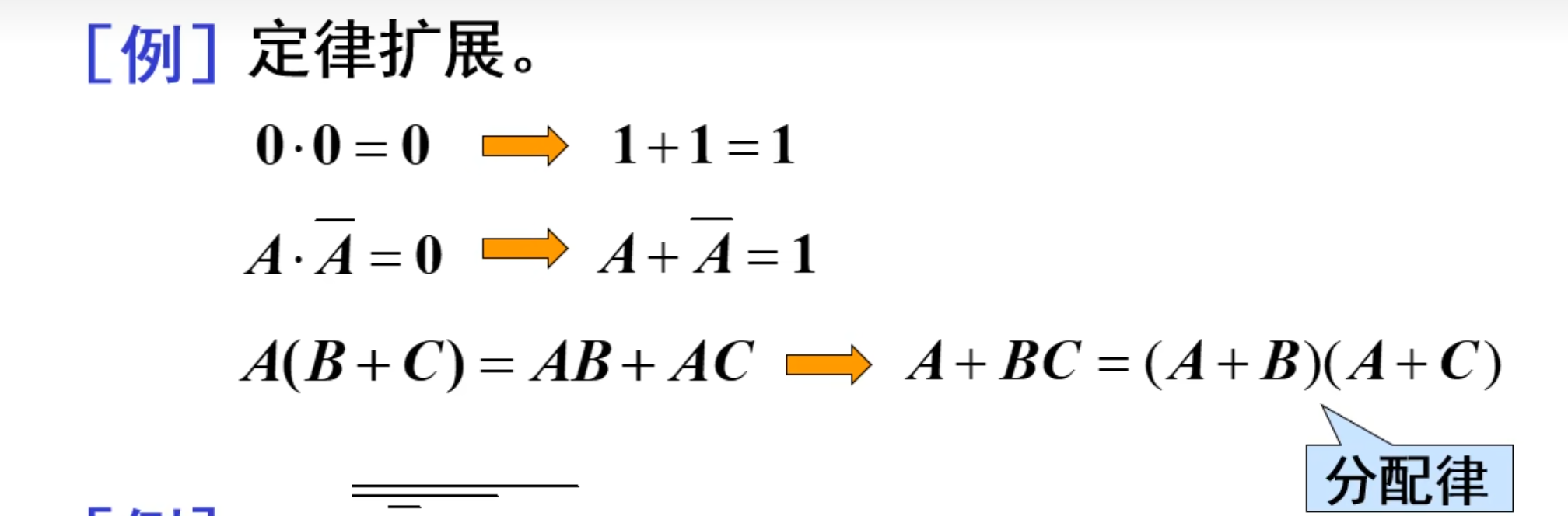
例题：

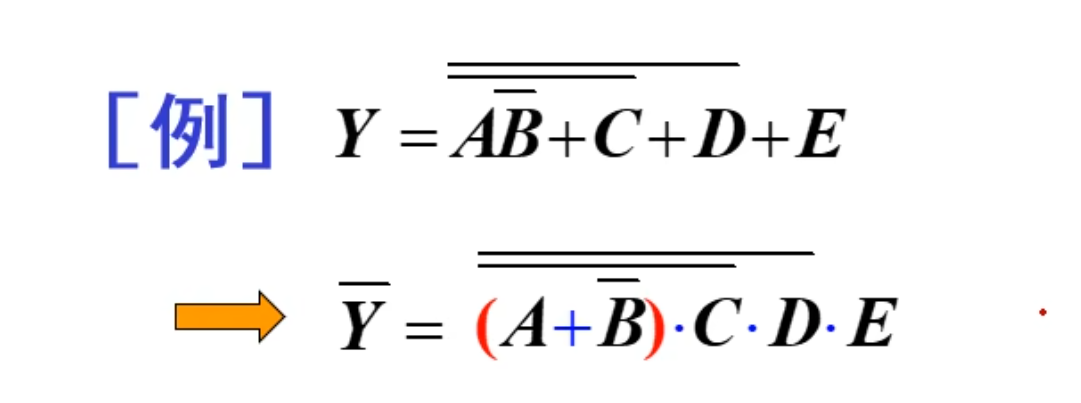
NOTE

利用对偶规则可以将基本公式和定律扩展一倍

逻辑函数的表达方法及其转换

逻辑函数的建立

下面利用这个例题来：

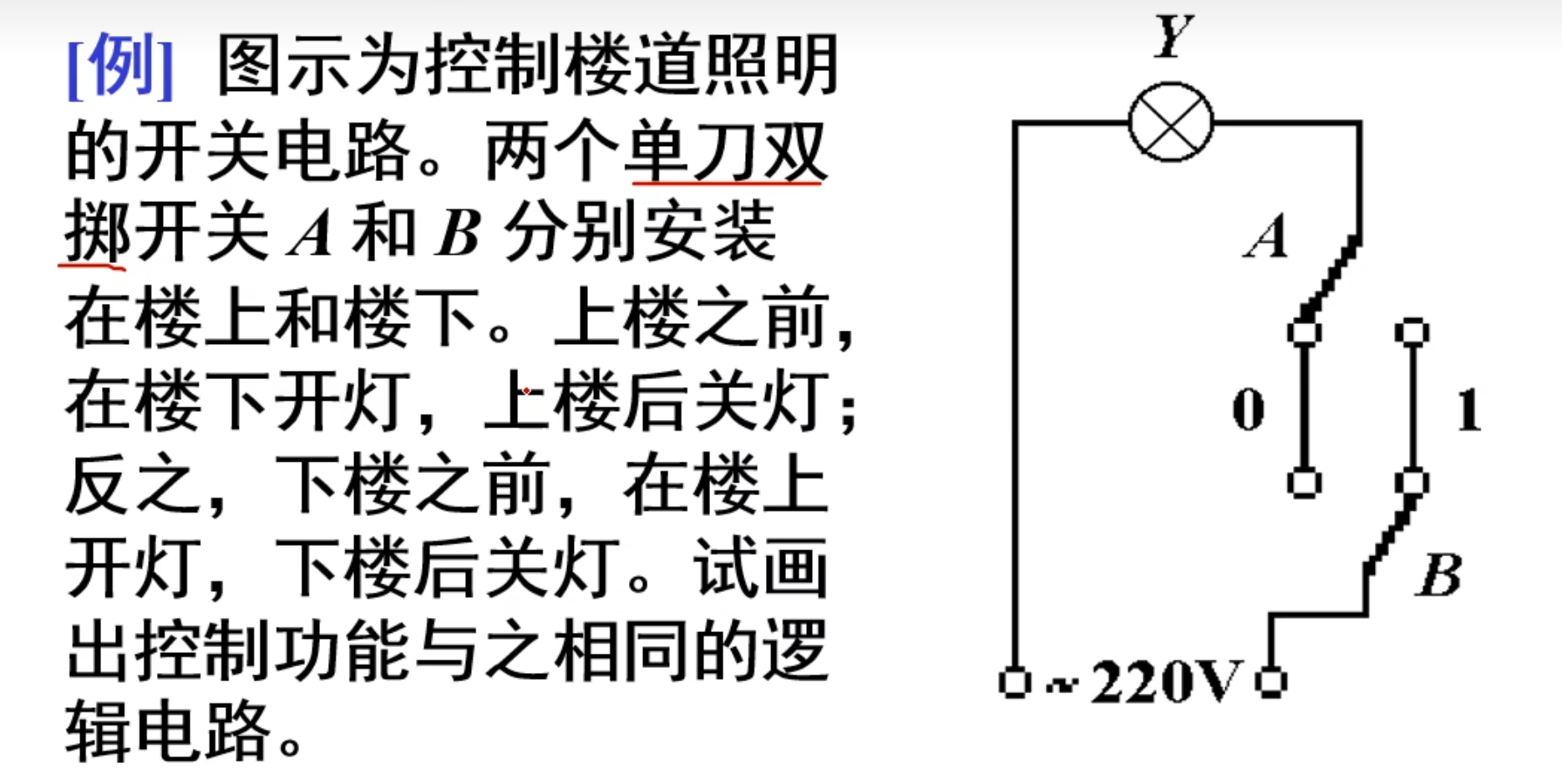
一、分析逻辑问题，建立逻辑函数的真值表

首先要找出输入变量和输出函数，对它们的取值做出逻辑规定，然后根据逻辑关系列出真值表。

在上面这个题中：

那么真值表就是：

很明显上面这个是一个同或

二、根据真值表写出逻辑式

$$Y=AB+\bar{A}\bar{B}=A\odot B=\overline{A\oplus B}$$

三、分析逻辑式以及画出逻辑图

分析逻辑式

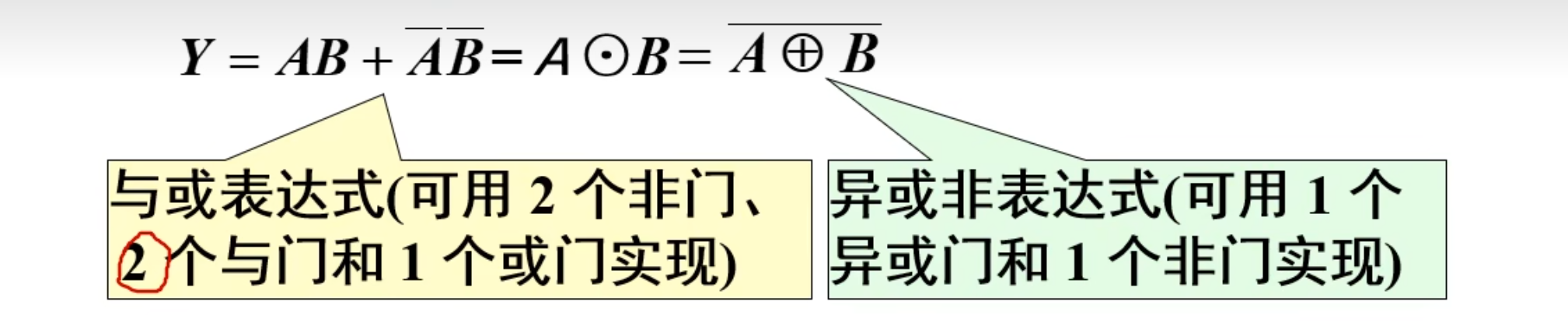
画逻辑图

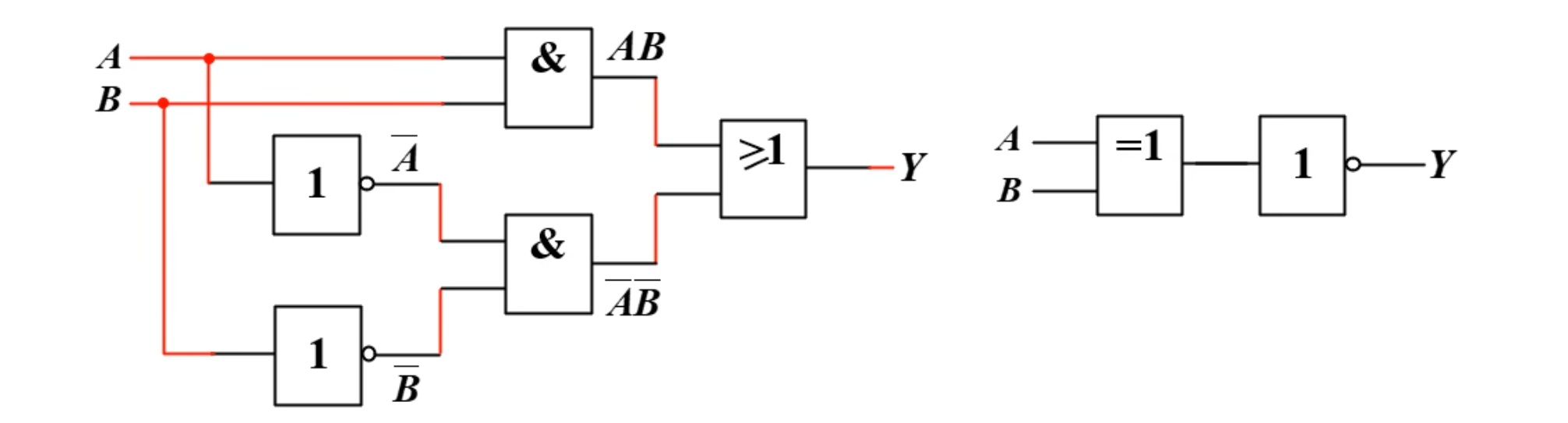
NOTE

设计逻辑电路的基本原则是使电路最简

逻辑函数的表示

NOTE

逻辑函数是用以描述数字逻辑系统输出与输入变量之间逻辑关系的表达式

换成表达式为： $Y=F(A,B,C,\cdots )$

逻辑函数由与、或、非 3 种基本逻辑运算构成

逻辑表达式

表示输出函数和输入变量逻辑关系的表达式，称为逻辑表达式，简称为逻辑式。

逻辑表达式一般根据真值表、卡诺图或者逻辑图写出。

常见表达形式

转换方法 ：

与 - 或表达式到与非 - 与非表达式

NOTE

主要方法是使用还原律（两次取反）

例如：

$$\begin{array}{rl}Y& =A\bar{B}+BC\\ & =\overline{\stackrel{―}{A\stackrel{―}{B}+BC}}\\ & =\overline{\stackrel{―}{A\stackrel{―}{B}}\cdot \stackrel{―}{BC}}\end{array}$$

上面第二行用的是还原律（两次取反），第三行用摩根定律

逻辑函数的标准表达式（最小项）

这里最主要的问题是最小项的问题。

IMPORTANT

最小项的定义：在逻辑函数中，如果一个与项（乘积项）包含该逻辑函数的全部变量，且每个变量以原变量或反变量形式只出现一次，则称该与项为最小项。对于 $n$ 个变量的逻辑函数共有 $2^n$ 个最小项。

最小项的基本性质

1. 对于变量的任一组取值，只有一个最小项的值为 1
2. 不同的最小项，使其值为 1 的那组变量取值也不同
3. 对于变量的同一组取值，任意两个最小项与的结果为 0
4. 对于变量的同一组取值，任意两个最小项或的结果为 1

最小项编号

最小项用 $m_i$ 表示，通常用十进制数作最小项的下标编号 $i$ 。编号方法是：将最小项中的原变量当作 1，反变量当作 0，则得一组二进制数，其对应的十进制数便为最小项的编号 $i$ 。

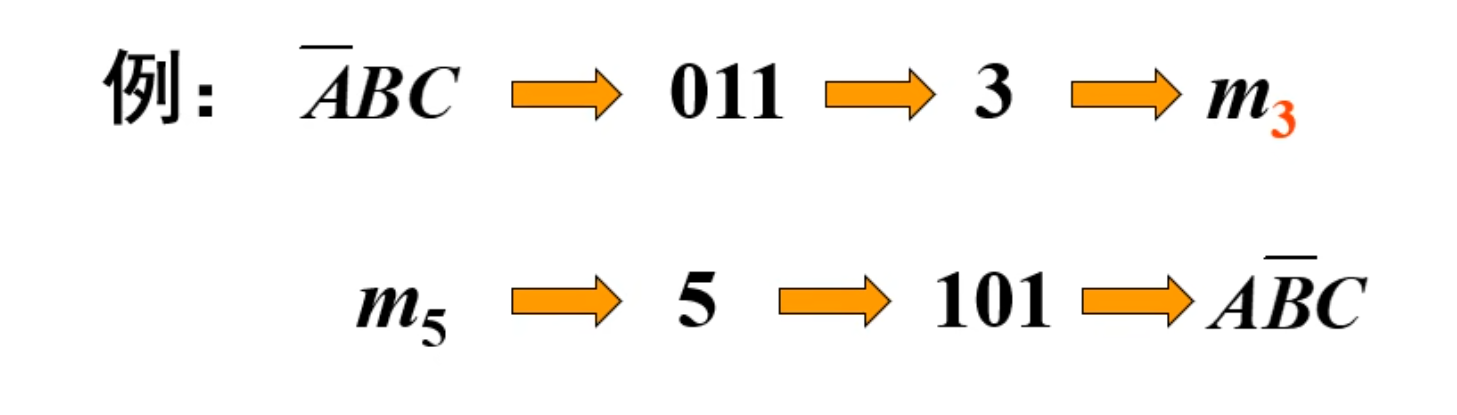
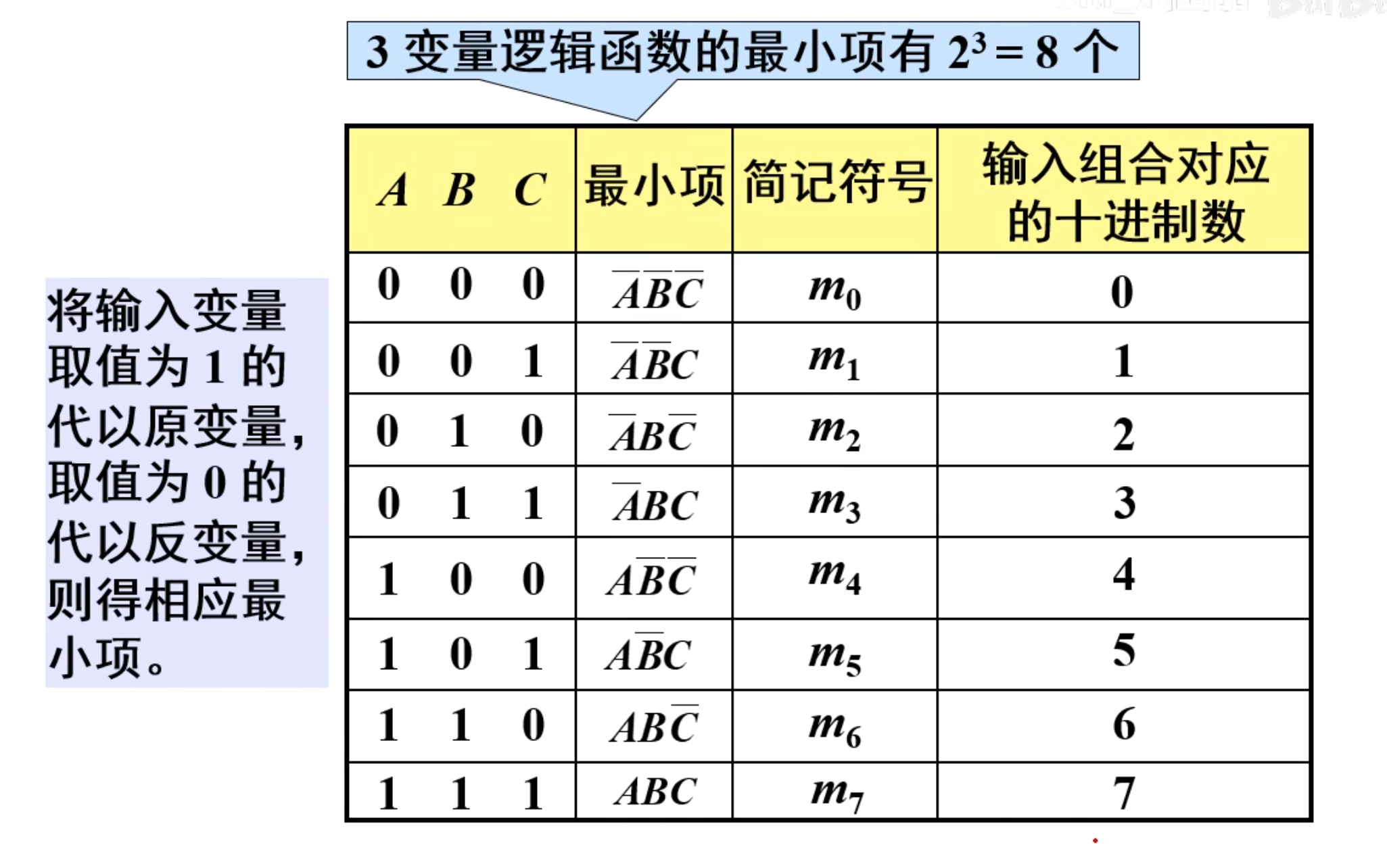
最小项表达式

这个就是标准与或表达式

任何逻辑函数都是由其变量的若干个最小项构成的，都可以表示成最小项之和的形式

而且这种形式是唯一的

NOTE

在与或表达式中，有时与项并不是最小项，可以利用 $\bar{A}+A=1$ 的形式来补充缺少的变量，将逻辑函数变成最小项之和的形式

例如下面这个：

$$Y=F(A,B,C)=AB+AC$$

结果：

$$\begin{array}{rl}\mathrm{Y}& =AB(\bar{C}+C)+\bar{A}C(\bar{B}+B)\\ & =AB\bar{C}+ABC+\bar{A}\bar{B}C+\bar{A}BC\\ & =m_1+m_3+m_6+m_7\\ & =\sum m(1,3,6,7)\end{array}$$

真值表

列出输入变量的各种取值组合及其对应输出逻辑函数值的表格称为真值表。

真值表能够直观的反应输出、输入变量的逻辑关系，在分析与设计电路时都要写出真值表。

列出真值表的方法有两种：

1. 按照 $n$ 位二进制数递增的方法列出输入变量的各种取值组合。

2. 分别求出各种组合对应的输出逻辑值填入表格

知道逻辑函数，求真值表以及结果

直接上例题：

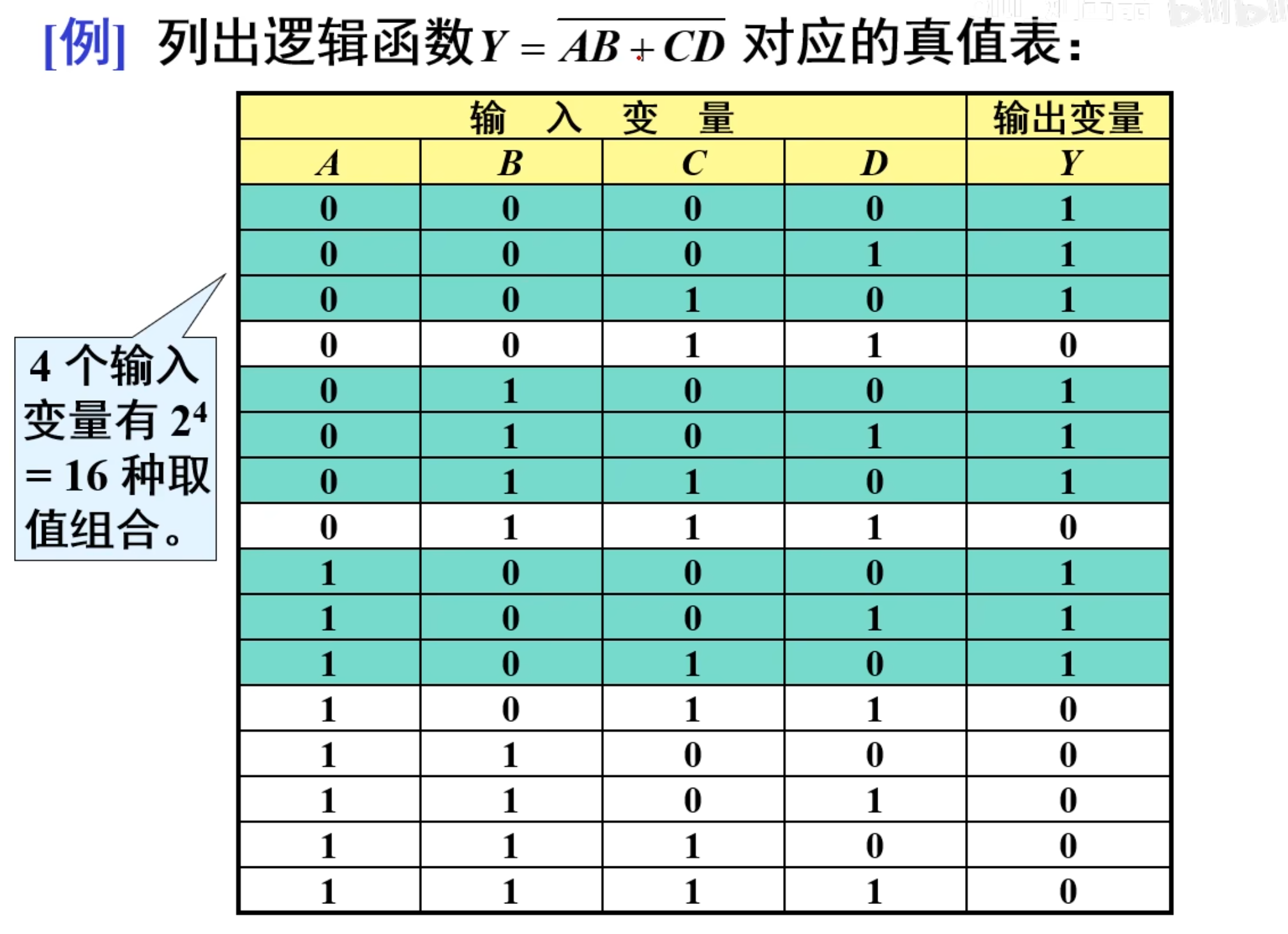
核心在于计算上面的公式中的逻辑运算。

知道真值表，求逻辑表达式。

方法如下：

1. 找出函数值为 1 的项。

2. 将输入变量取值为 1 的用原变量代替，取值为 0 的用反变量代替，则得到一系列与项。

3. 将这些与项相加（相或）就得到逻辑式

例题：

逻辑图*

逻辑图是由逻辑符号以及相应连线构成的电路图。

逻辑图一般根据逻辑式画出，将各级逻辑运算用相应的门电路实现

直接上例题：

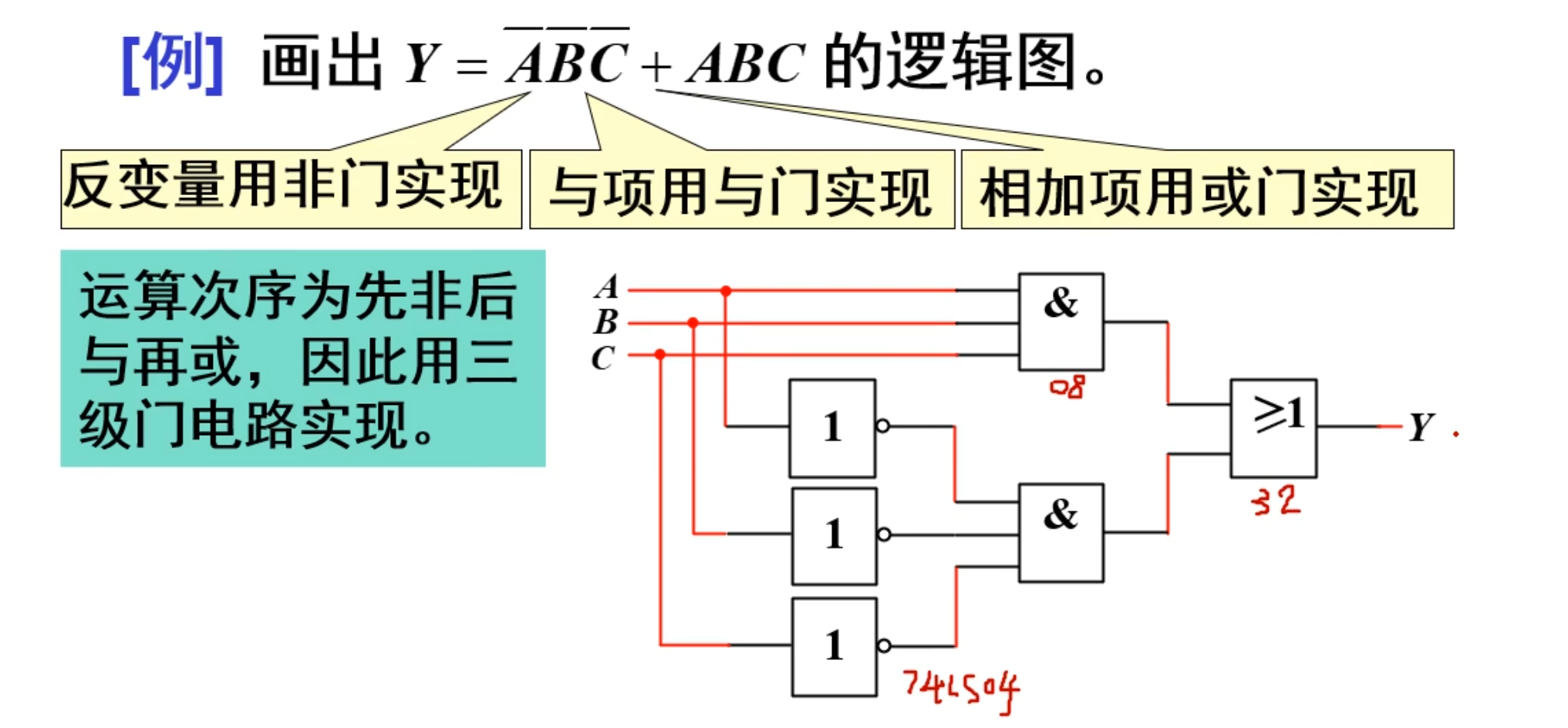
NOTE

画图的时候，要注意美观问题

当然，最重要的是，这部分考试会经常考，要多注意

波形图

波形图代表输入变量和对应的输出变量随时间变化的波形。

画波形图的时候需要注意，其横坐标是时间轴，纵坐标是变量取值，由于变量取值只有 0 和 1，一般在图中不用标出坐标轴，但输入、输出变量要对应画出。如下图所示。

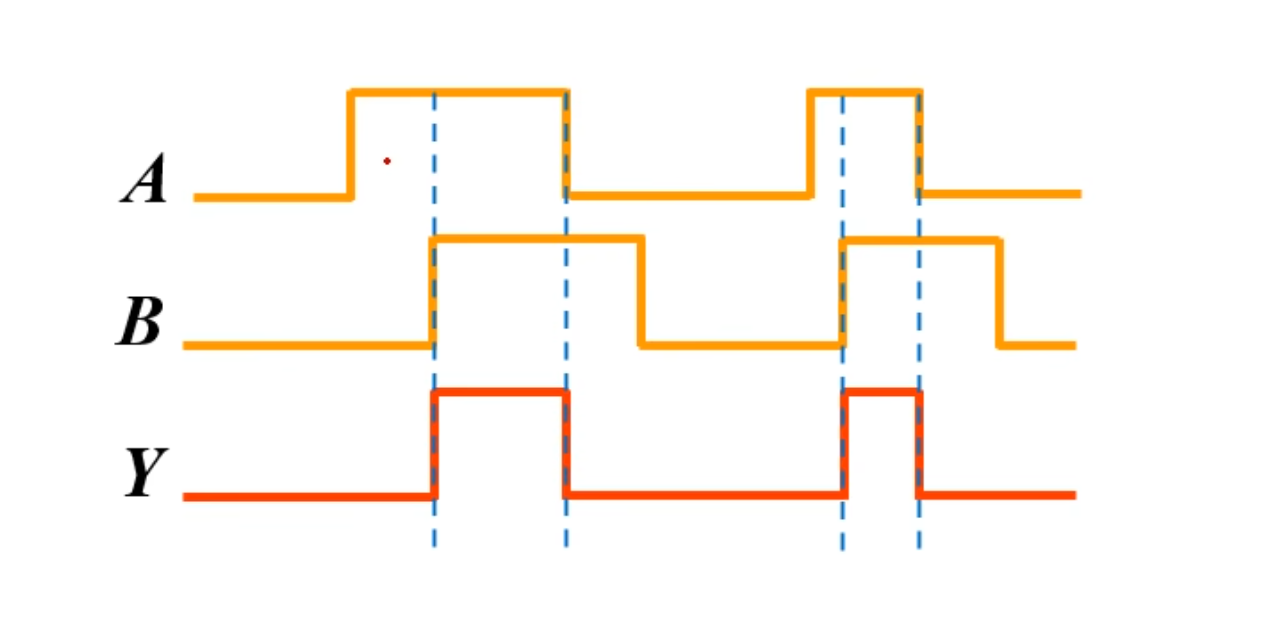
当然，主要问题是从波形图到逻辑表达式的转换是如何的。

其次，反过来从逻辑表达式转换到波形图，也是需要解决的问题。

例题：

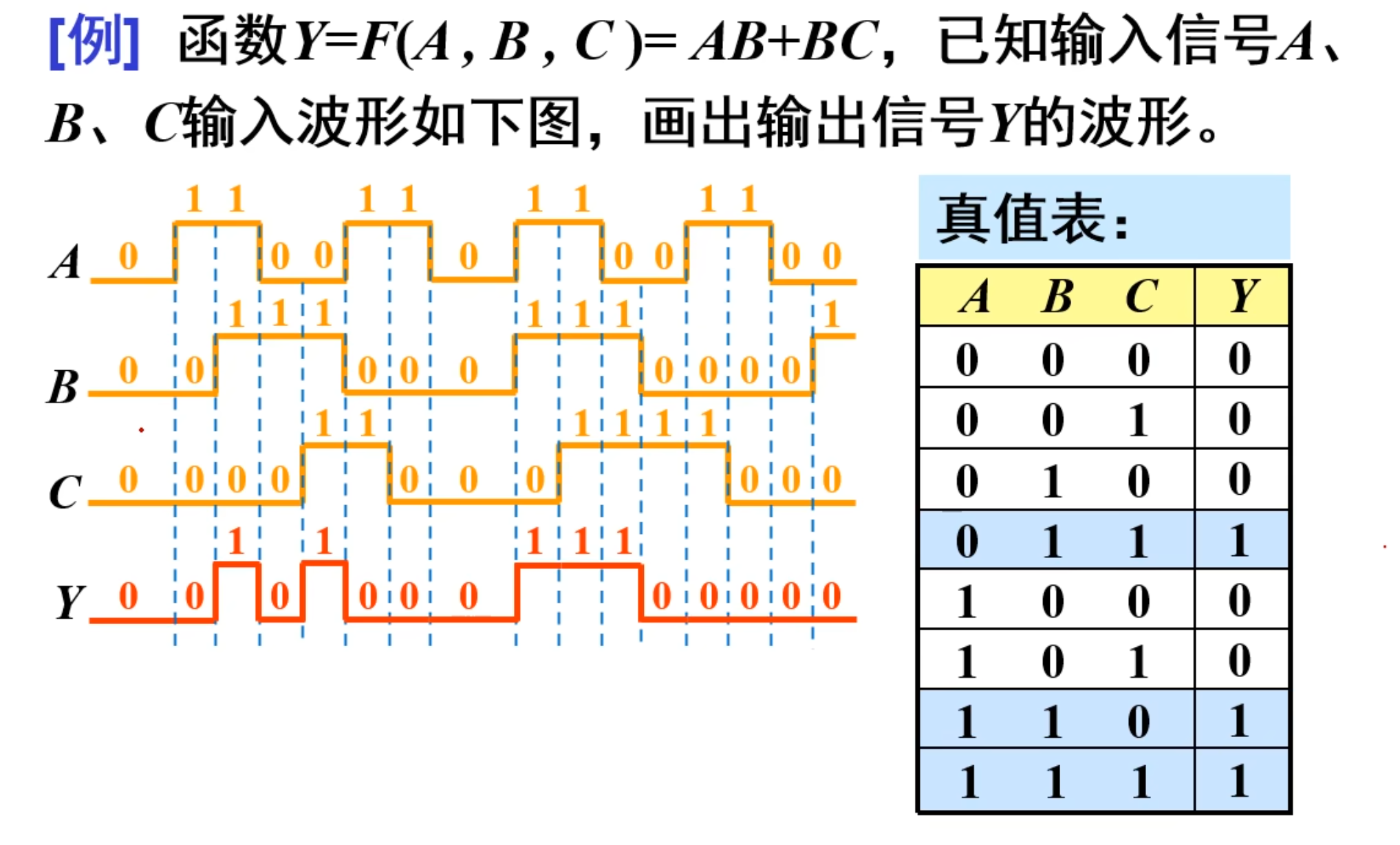
逻辑函数的化简

逻辑函数化简的意义与标准

其主要意义在于让逻辑式最简，以便设计出最简的逻辑电路，从而节省元器件、优化生产工艺、降低成本和提高系统可靠性。

直接上例题：

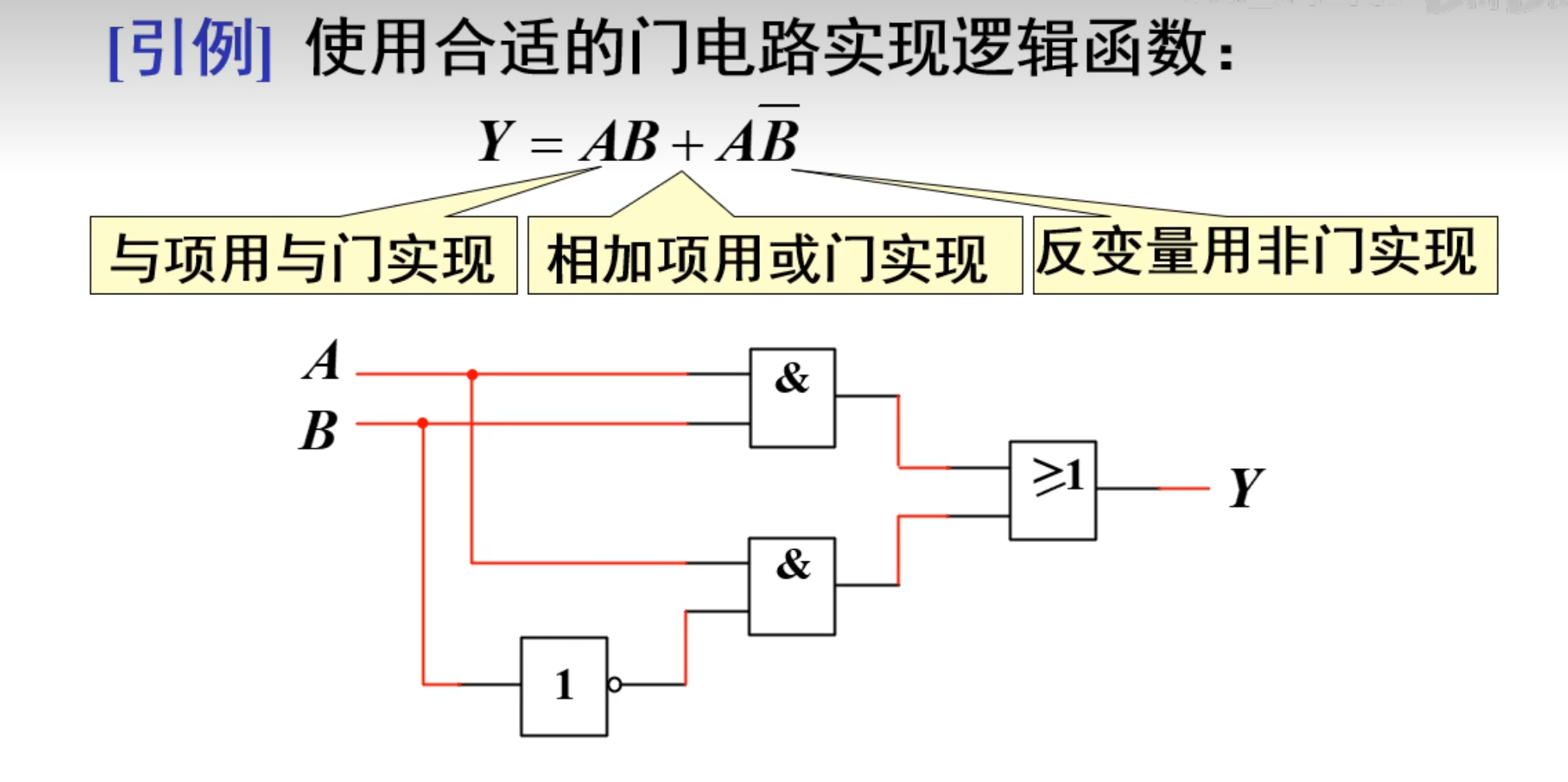
很明显，上面的电路比较复杂，所以尽可能的对其进行化简。

直接将公式化简：

$$Y=AB+A\bar{B}=A(B+\bar{B})=A$$

而得到的结果不需要任何门电路。

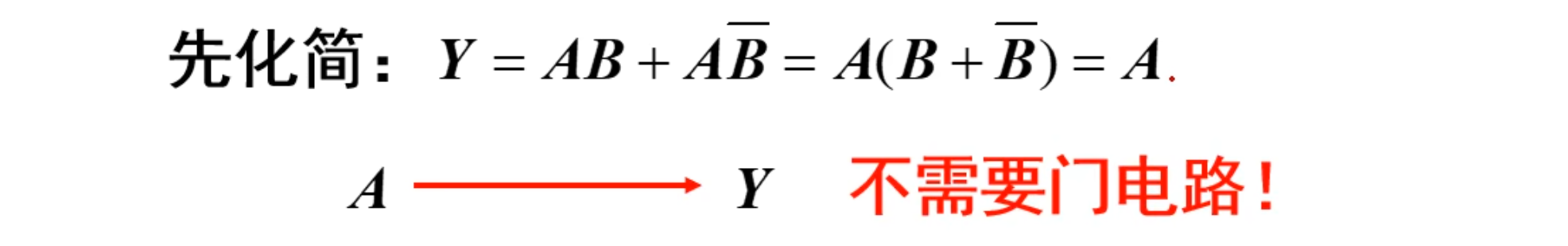
NOTE

不同形式的逻辑式有不同的最简式，一般要先求取最简与或式，然后通过变换得到所需要的最简式。

最简与或式：

1. 乘积项（即与项）的个数最少，使与门个数最少。

2. 每个乘积项中的变量数最少，使与门的输入端最少。

最简与非 - 与非式

1. 非号个数最少，使得与非门个数最少

2. 每个非号中的变量数最少，使与非门的输入端数最少。

NOTE

主要方法是使用还原律（两次取反）

在 常见表达形式 中提到

逻辑函数的公式化简法

这个主要是运用逻辑代数的基本定理和公式来对逻辑表达式进行化简

并项法

运用 $AB+A\bar{B}=A(B+\bar{B})=A$ ，将两项合并为一项，并消去一个变量。

例题：

$$Y_1=A\bar{B}C+A\bar{B}\bar{C}=A\bar{B}(C+\bar{C})=A\bar{B}$$$$\begin{array}{rl}{Y}_2& =A(BC+\bar{B}\bar{C})+A(\underset{―}{B\bar{C}+\bar{B}C})\\ & =A\overline{B\oplus C}+A(B\oplus C)\\ & =A\end{array}$$

吸收法

运用 $A+AB=A(1+B)=A$ 和 $AB+\bar{A}C+BC=AB+\bar{A}C$ ，消去多余的与项。

上面这句话中的第一个公式还好理解，主要是第二个

其实就是之前学到的冗余律

例如：

$$Y_1=AB+AB(E+F)=AB(1+E+F)=AB$$$$\begin{array}{rl}{Y}_2& =\overline{AB}+\bar{A}D+\bar{B}E\\ & =\bar{A}+\bar{B}+\bar{A}D+\bar{B}E\\ & =(\bar{A}+\bar{A}D)+(\bar{B}+\bar{B}E)\\ & =\bar{A}+\bar{B}\\ & =\overline{AB}\end{array}$$

上面的 $Y_2$ 主要是用了摩根定律。

$$Y_3=\bar{A}B+AC+\bar{B}\cdot \bar{C}+A\bar{B}+\bar{A}\cdot \bar{C}+BC=\bar{A}B+AC+\bar{B}\cdot \bar{C}$$

这道题目用的就是[冗余律]，当然用同一种方法，但是过程不一样，得到最后的结果也可能不一样

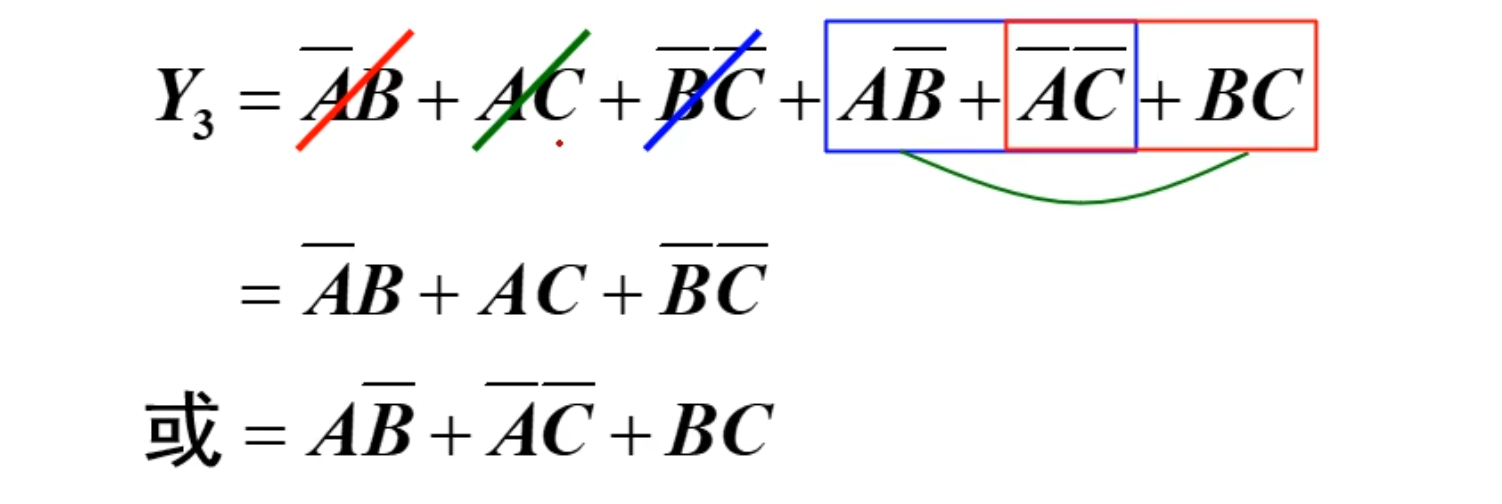
最后可以使用真值表来判断是否相等。

IMPORTANT

逻辑函数化简结果不唯一，但是结果真值表肯定一样。

消去法

运用 $A+\bar{A}B=A+B$ 或者 $\bar{A}+AB=\bar{A}+B$ ，消去多余因子

例如：

$$Y_1=\bar{A}+AB+\bar{B}C=\bar{A}+B+\bar{B}C=\bar{A}+B+C$$$$\begin{array}{rl}{Y}_2& =\overline{AB}+AC+BD=\bar{A}+\bar{B}+AC+BD\\ & =(\bar{A}+AC)+(\bar{B}+BD)\\ & =\bar{A}+\bar{B}+C+D\\ & =\overline{AB\stackrel{―}{C}\stackrel{―}{D}}\end{array}$$$$\begin{array}{rl}{Y}_3& =AB+\bar{A}C+\bar{B}C\\ & =AB+(\bar{A}+\bar{B})C\\ & =AB+\overline{AB}C\\ & =AB+C\end{array}$$

上面第二行用到了摩根定律

配项法

在函数某一项乘以 $A+\bar{A}=1$ ，将一项展开两项，或利用 $A\mathit{B}+\bar{A}C=A\mathit{B}+\bar{A}C+\mathit{B}C$ ，增加冗余项 $BC$ 。

例题：

$$\begin{array}{rl}{Y}_1& =AB+\bar{B}\bar{C}+A\bar{C}D\\ & =AB+\bar{B}\bar{C}+A\bar{C}D(B+\bar{B})\\ & =AB+\bar{B}\bar{C}+AB\bar{C}D+A\bar{B}\bar{C}D\\ & =(AB+AB\bar{C}D)+(\bar{B}\bar{C}+A\bar{B}\bar{C}D)\\ & =AB+\bar{B}\bar{C}\end{array}$$

其实上面这道题不需要这么麻烦的。直接使用冗余律就可以

$$\begin{array}{rl}{Y}_1& =AB+\bar{B}\bar{C}+A\bar{C}D\\ & =BA+\bar{B}\cdot \bar{C}+A\bar{C}D\\ & =BA+\bar{B}\cdot \bar{C}\end{array}$$

第二个：

$$\begin{array}{r}{Y}_2=A\bar{B}+\bar{A}B+B\bar{C}+\bar{B}C\end{array}$$

这道题目是否是最简单形式不太确定，其直观性不强。

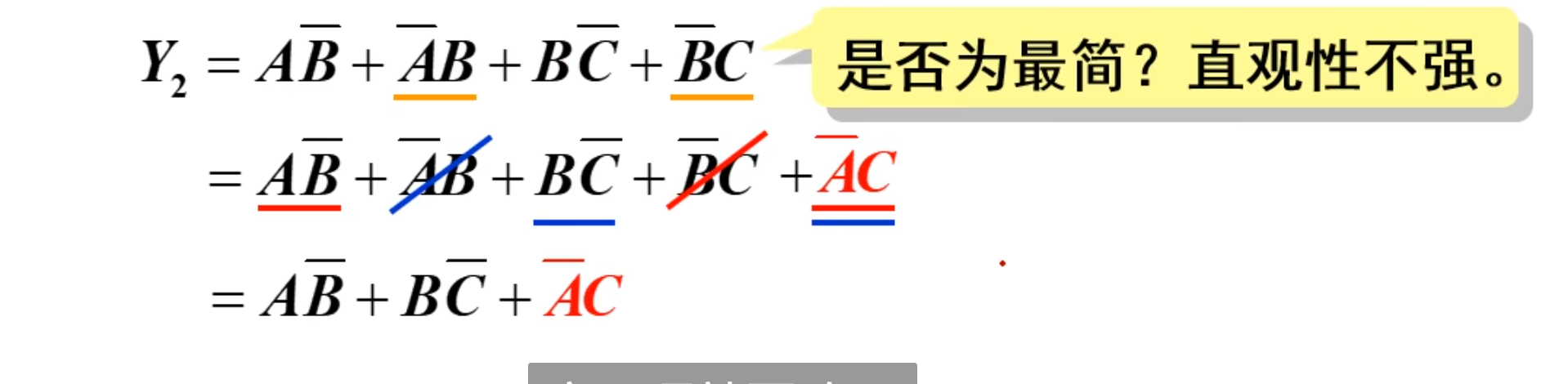
主要是使用冗余律的逆用，得到的结果就是这样的。

当然还可以针对第一个和第三个来逆用冗余律

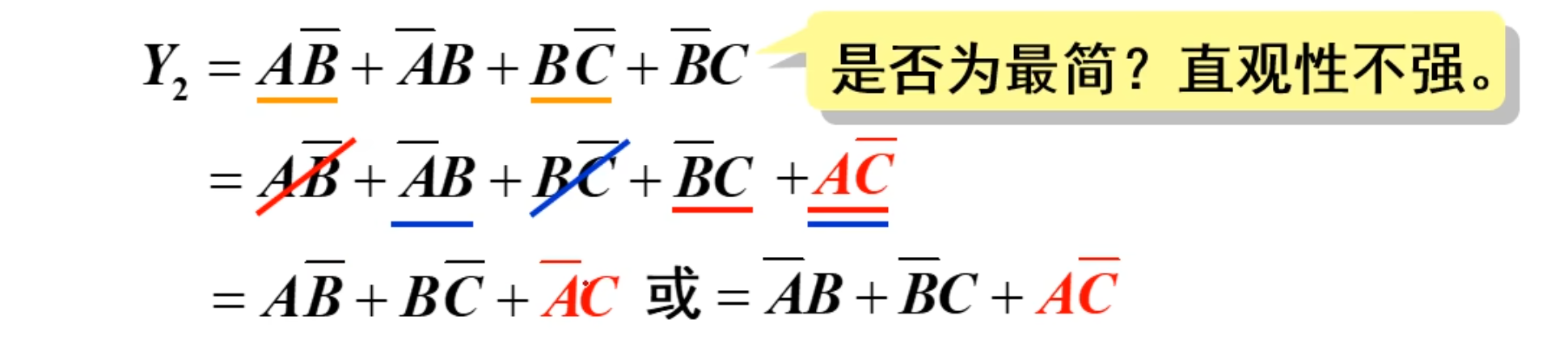
化简结果是不唯一的。

综合运用

$$\begin{array}{rl}{Y}_1& =AD+A\bar{D}+AB+\bar{A}C+BD+ACEF+\bar{B}E+DEF\\ & =A(D+\bar{D}+B+CEF)+\bar{A}C+BD+\bar{B}E+DEF\\ & =A+\bar{A}C+BD+\bar{B}E+DEF\\ & =A+C+BD+\bar{B}E+DEF\\ & =A+C+BD+\bar{B}E\end{array}$$

上面的第三行是消去法，第四行到第五行是使用了吸收法

再来一个例题：

$$\begin{array}{rl}{Y}_2& =AC+\bar{A}D+\bar{B}D+B\bar{C}\\ & =AC+B\bar{C}+(\bar{A}+\bar{B})D\\ & =AC+B\bar{C}+\overline{AB}D\\ & =AC+B\bar{C}+AB+\overline{AB}D\\ & =AC+B\bar{C}+AB+D\\ & =AC+B\bar{C}+D\end{array}$$

上面的第三行到第四行是逆向使用冗余律，然后与后面哪一项使用消去律。最后再把冗余项吸收进去。

NOTE

拿到题目之后，先看有没有能合并的，然后再看一下有什么可以拆开的，然后看下有没有可以消去的，最后看看能不能添加一个冗余项

使用公式法化简很难判定结果是否为最简，不够直观。

卡诺图化简*

最小项卡诺图的组成

相邻最小项

两个最小项中只有一个变量互为反变量，奇遇变量均相同，称为相邻最小项，简称为相邻项

相邻最小项的重要特点是：

两个相邻最小项相加（相或）可合并为一项，消去互反变量

$$ABC+AB\bar{C}=AB(C+\bar{C})=AB$$

卡诺图的组成

1. $n$ 个变量，有 $2^n$ 个最小项，每个最小项都要用 $1$ 个小方格表示。
2. 按循环码的编码顺序（格雷码）排列这个是关键，使相邻最小项在几何位置上也相邻且循环相邻

二变量卡诺图

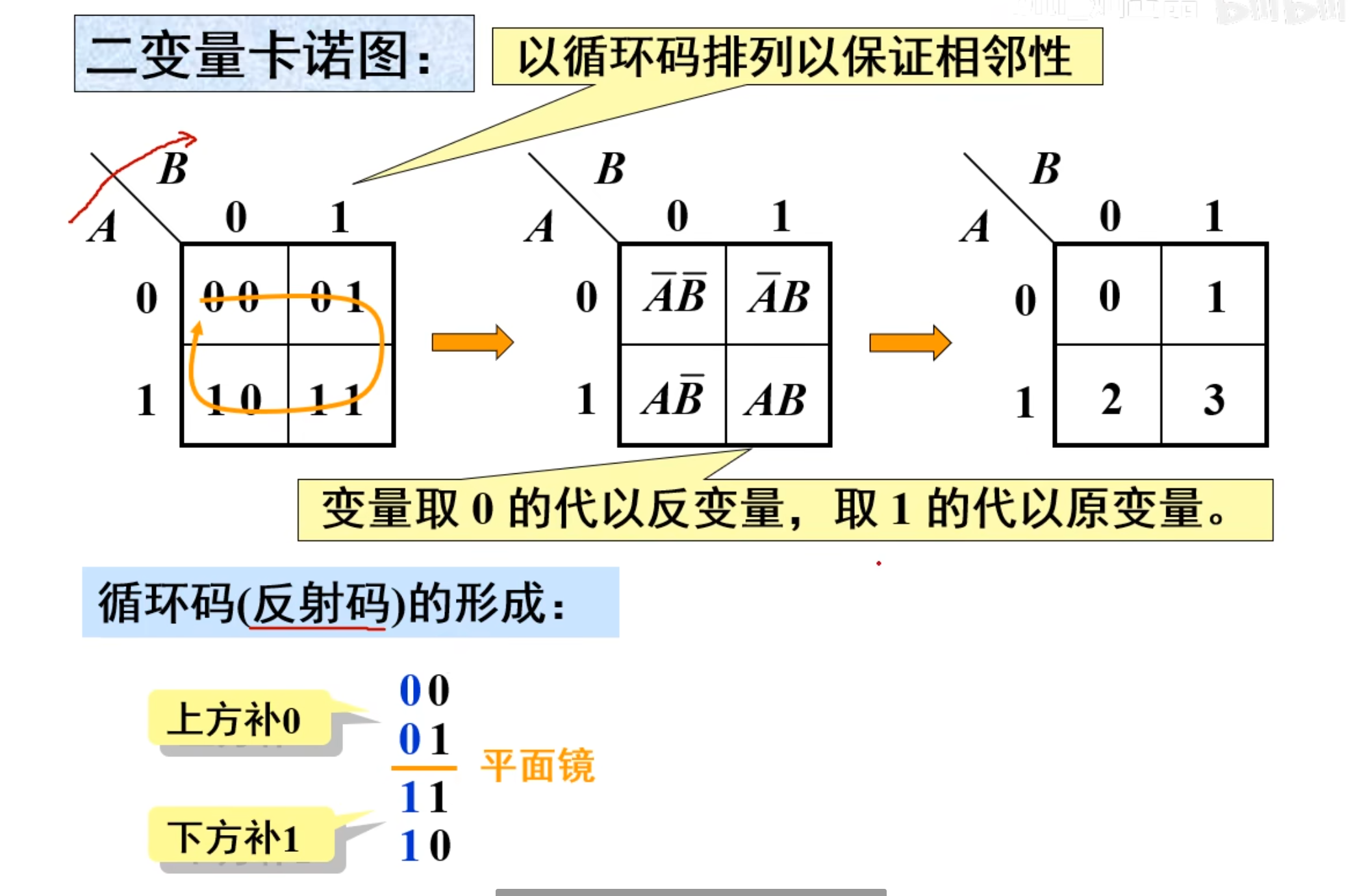
画卡托图的时候，左上角是按照顺时针的方式去写的，比如 $AB$ ，左边就是 $A$ ，右边就是 $B$ ，当然，读的时候也是按照顺时针的方法去读的。

需要注意的是，循环码的方法，是每次只有一个变量与上一个不同，从 $0$ 开始。

可以看到循环码是按照镜像的方法得到的，上面补 0，下面补 1；得到的正好是卡诺图顺时针读到的数。

而上面图中的第三个图则是用 $m_i$ 的形式来表示的。

三变量卡诺图

如果这八个格子是有 4 列，则把后两个变量放到一起，如果这个八个格子有四行，则把前两个变量放到一起。

而这个反射码则是将二变量得到的反射码镜像一下，然后在上面补 0，下面补 1。这样就得到了最后的结果。这个结果就是卡诺图中顺时针写出来的。

同时，需要特别注意下面这个图，后续用的次数非常多，比较难区分的就是顺序

四变量卡诺图

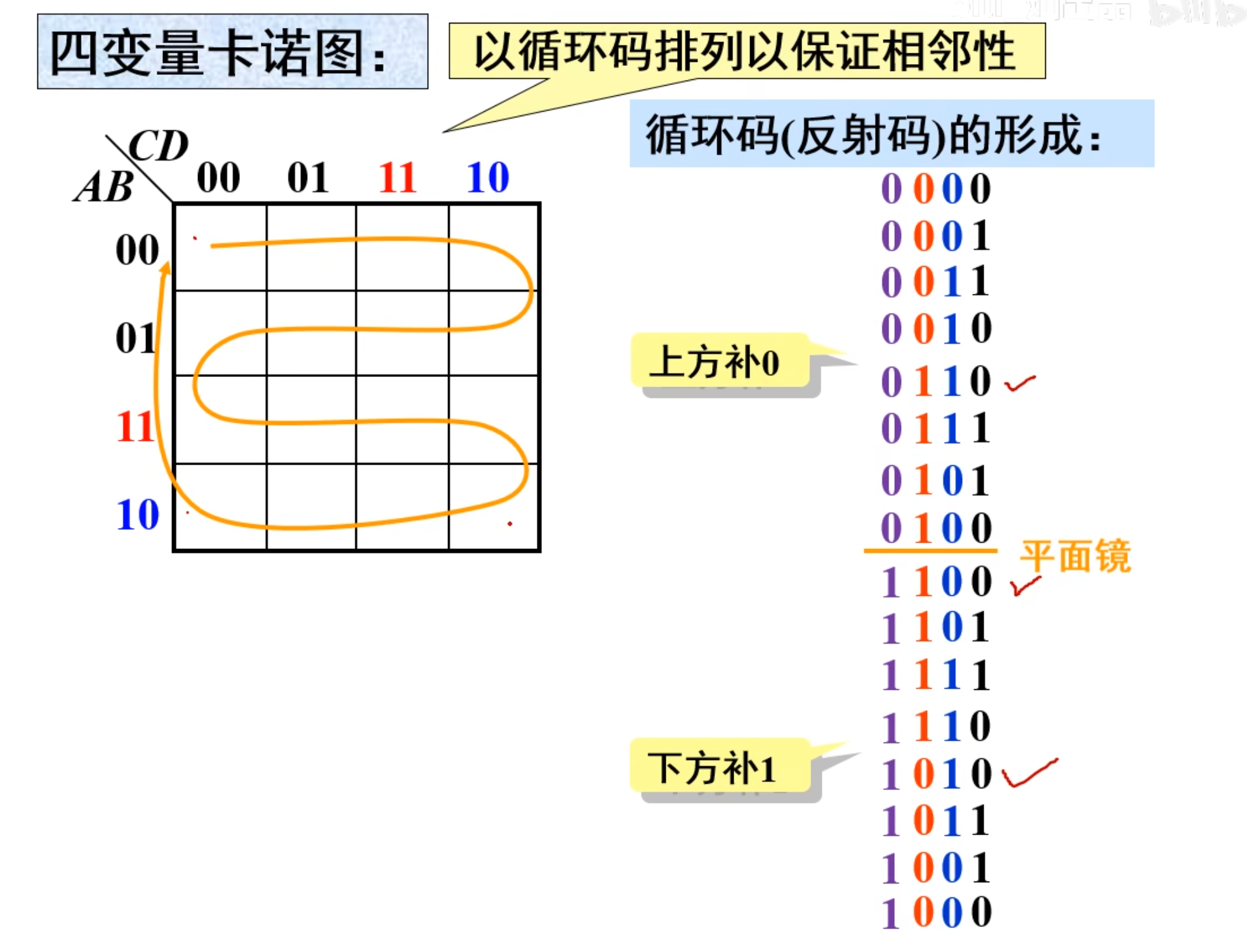
四变量卡诺图的循环码，同样的，是由三变量镜像之后，上面补 0，下面补 1 得到的。

而书写顺序则是两个顺时针圆圈。（如上面图中是黄线所示）

然后再用最小项的方法写出来就是下面这个图（非常重要，需要记住）

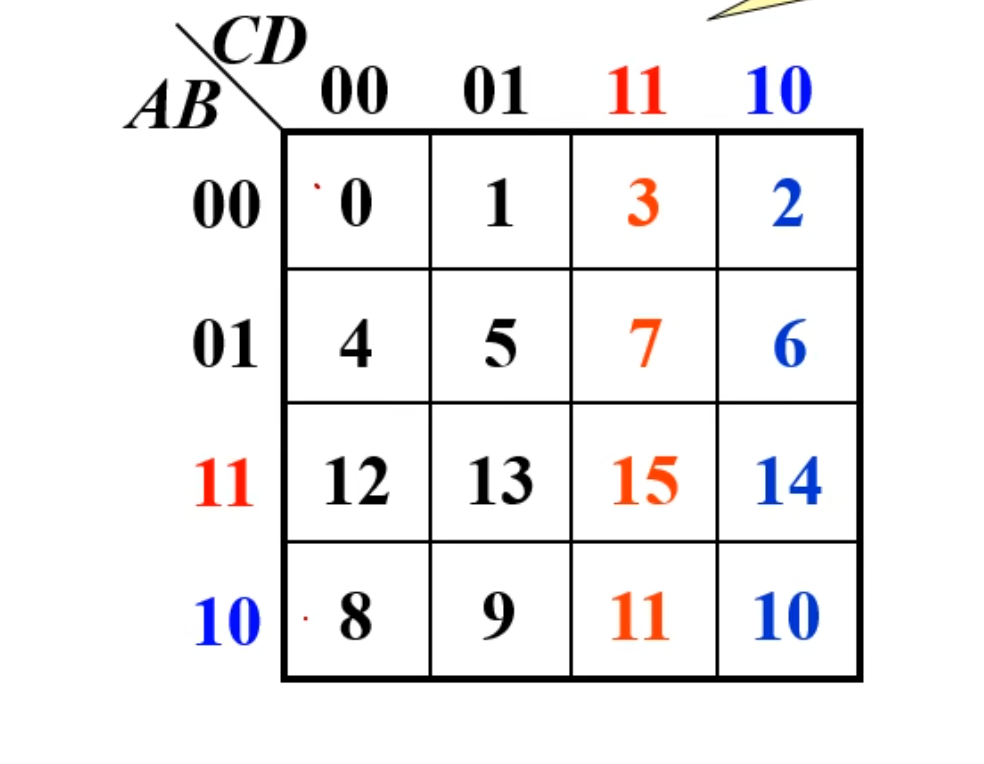
对于上面这个图，最需要注意的地方是注意 8 所在的哪一行（在最后一行，而不是倒数第二行）

卡诺图中的相邻项（几何相邻）

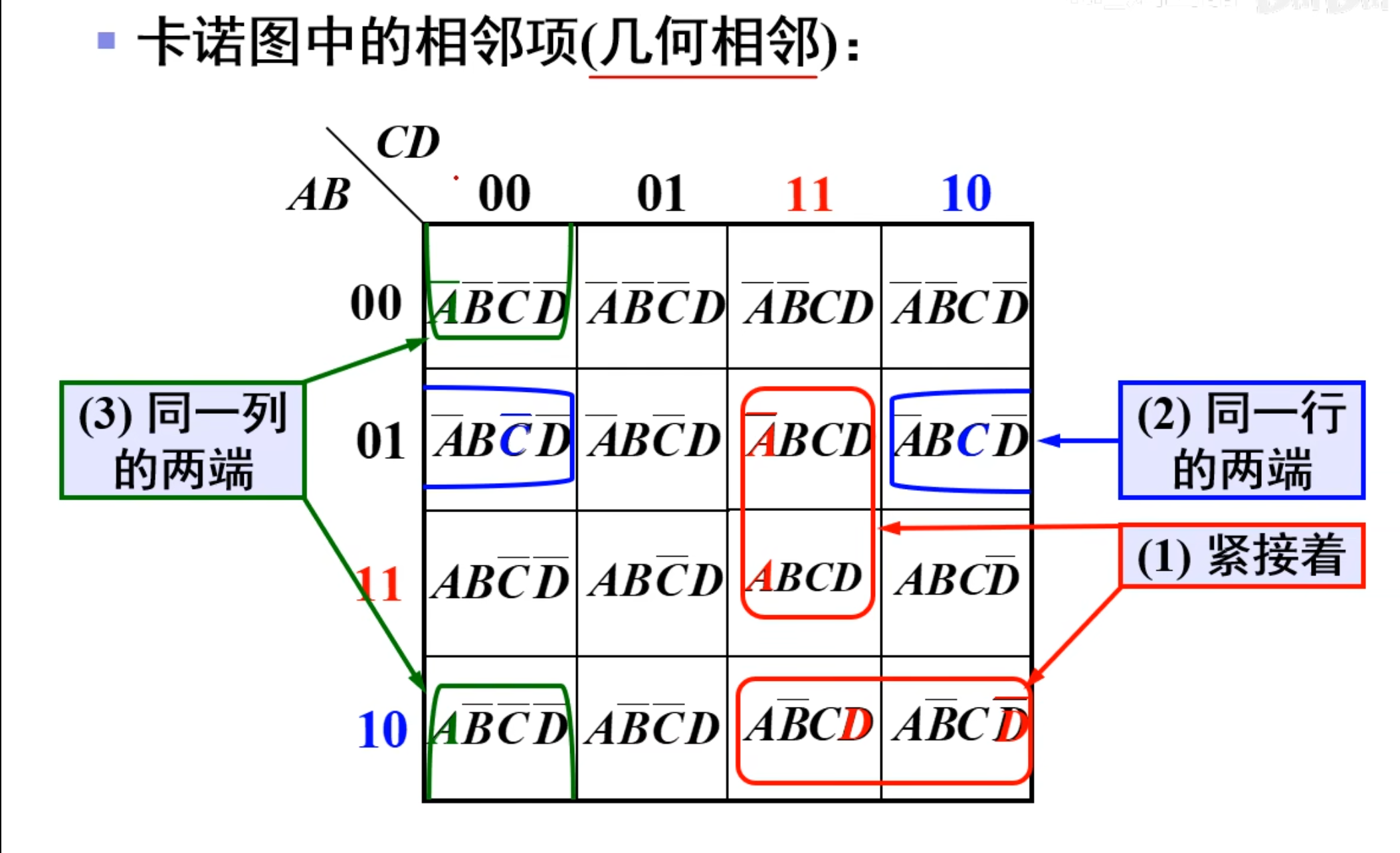
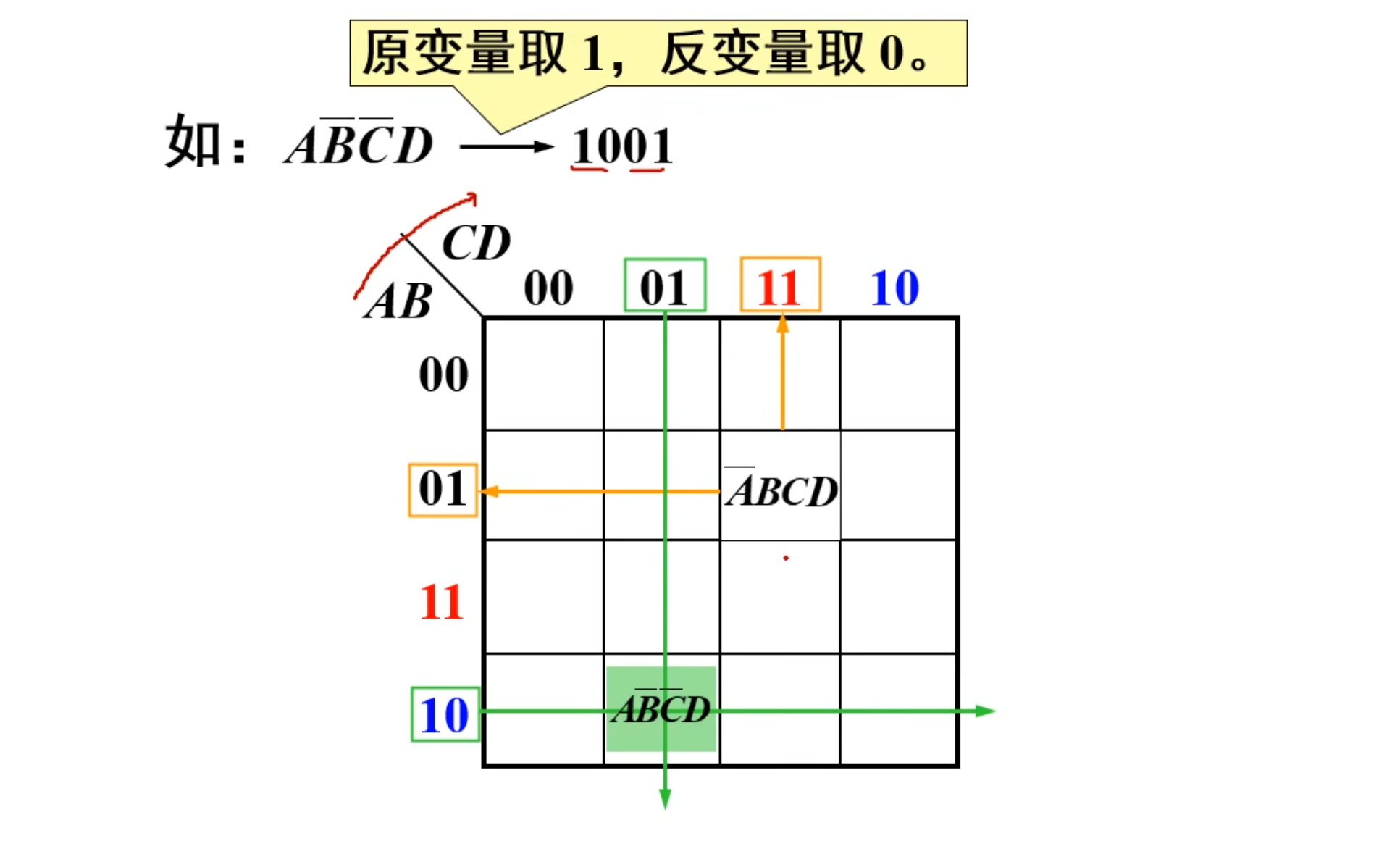
来个题目： 已知最小项如何找对应小方格？如何写出卡诺图方格对应的最小项。

如 $A\bar{B}\bar{C}D$

用卡诺图表示逻辑函数*

NOTE

基本步骤：

首先求逻辑函数的真值表、标准或一般与或式；

根据变量个数画出变量卡诺图

根据真值表、标准或一般与或式来填写卡诺图。

直接上例题：

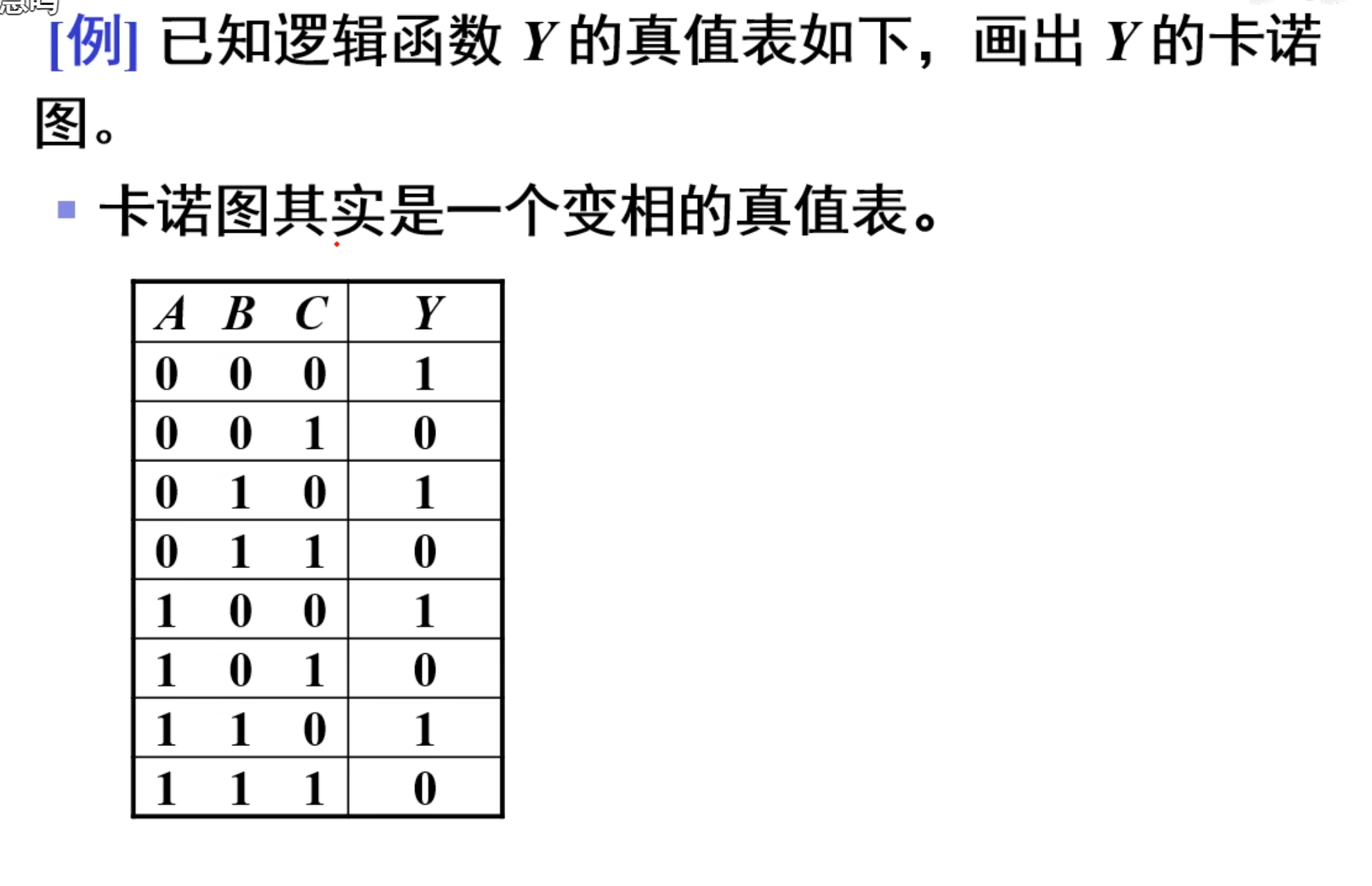
IMPORTANT

卡诺图其实就是一个变相的真值表。

解题步骤：

首先是根据题目中的真值表，画出卡诺图。

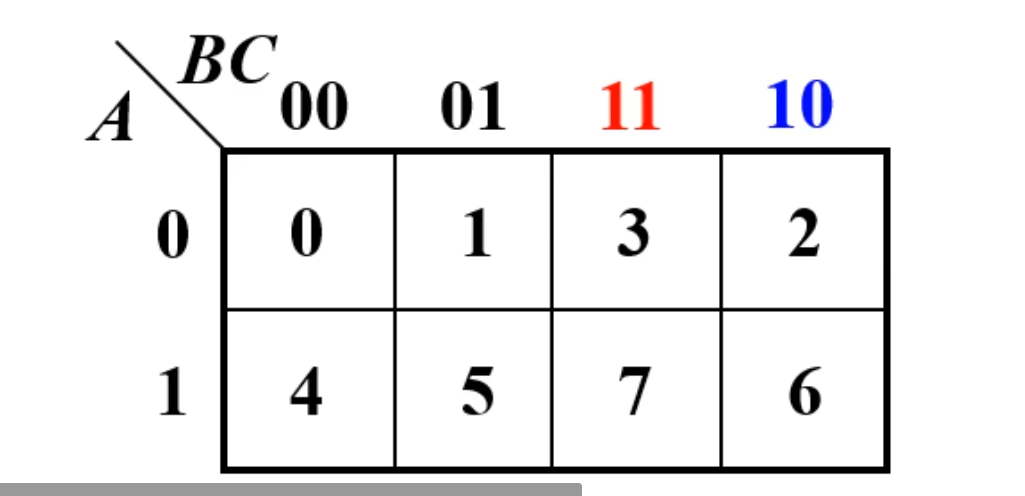
然后找出真值表中 $Y=1$ 对应的最小项，在卡诺图相应方格中填 $1$ ，其他部分不写任何东西。

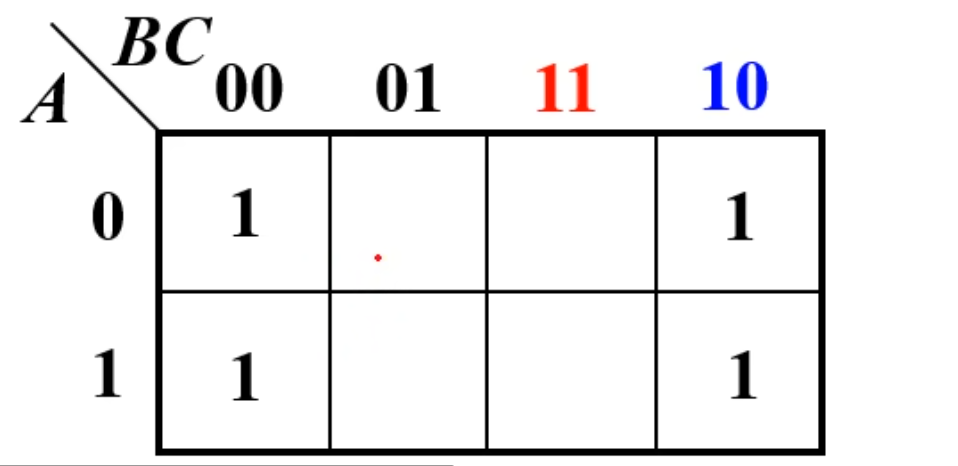
上面得到的这个卡诺图就是最后的结果。

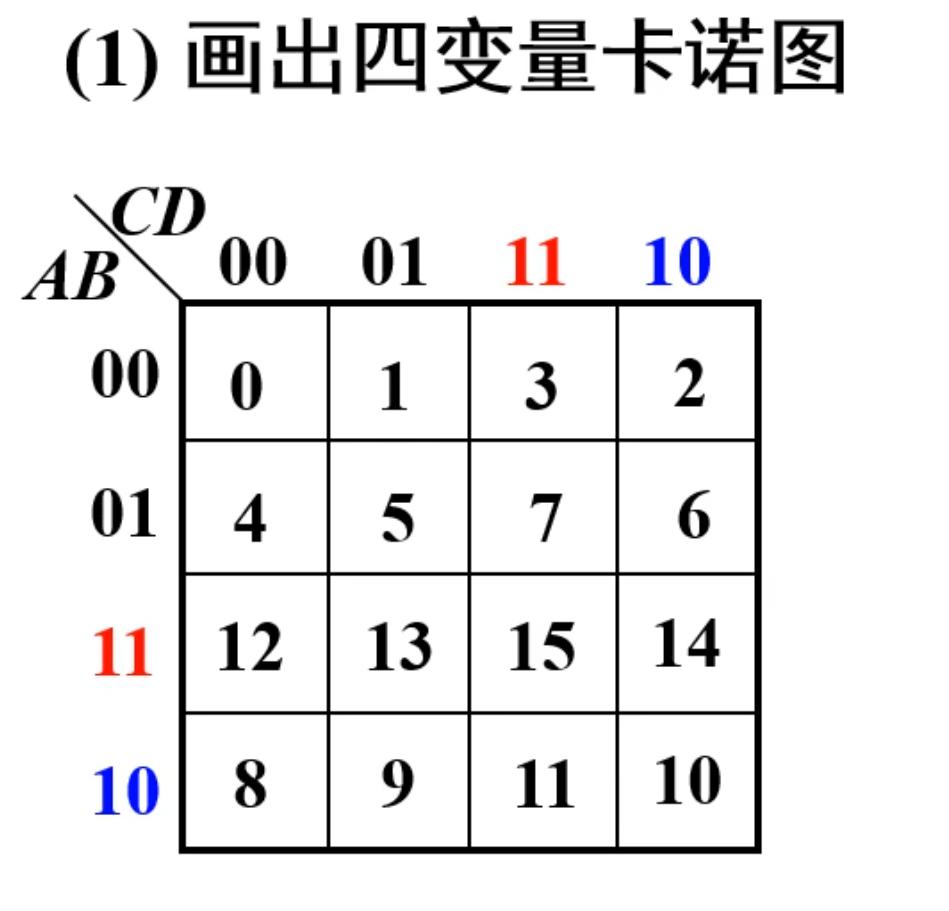
然后再来看一个例题：

注意到，上面的 $\sum m(0,1,12,13,15)$ 是最小项之和。这个逻辑函数是标准与或式。

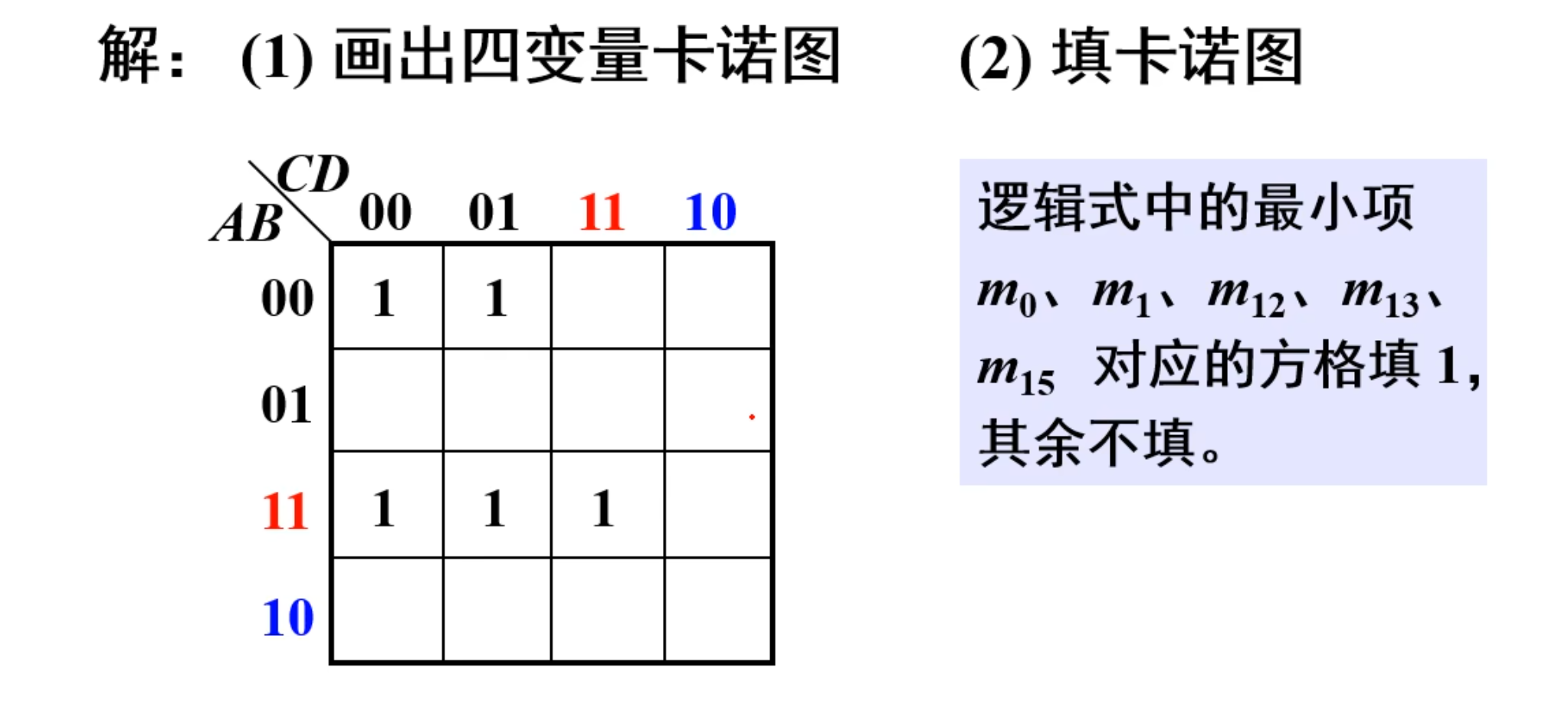
当然，首先要做的是先把基础卡诺图画出来。

然后要做的是，将逻辑式中的最小项 $m_0、m_1、m_{12}、m_{13}、m_{15}$ 对应的方格填上 1，其他的方格不写任何东西。

再来一个难题：

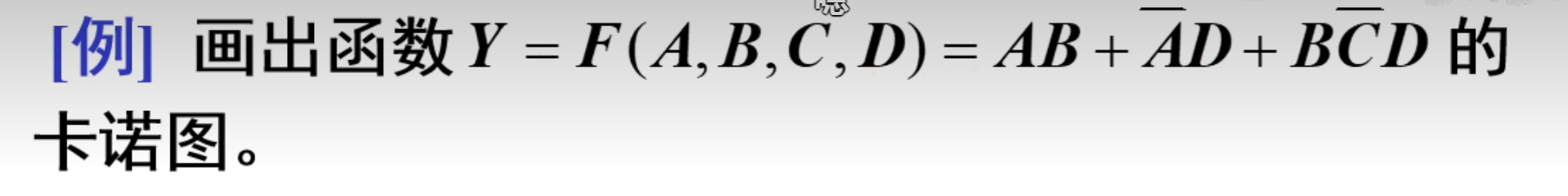
上面这个很明显不是一个标准与或式，需要先将其换成标准与或式，或者直接不转换，直接在图上进行找交集

首先是画出标准的四变量卡诺图。然后找交集。

首先看第一个变量 $AB$ ，这个代表着 $CD$ 可以任意取值。

再看第二个变量 $\bar{A}D$ ，这个代表着可以同时满足 $A=0$ ， $D=1$ 的小方格。

最后看最后一个变量 $B\bar{C}D$ ，这个代表着可以满足 $B=1$ ， $C=0$ ， $D=1$ 的小方格。

最后的结果如下：

卡诺图化简逻辑函数*

化简依据

其原理在于利用卡诺图的相邻性，对相邻最小项进行合并，消去互反变量，以达到化简的目的。

化简规律

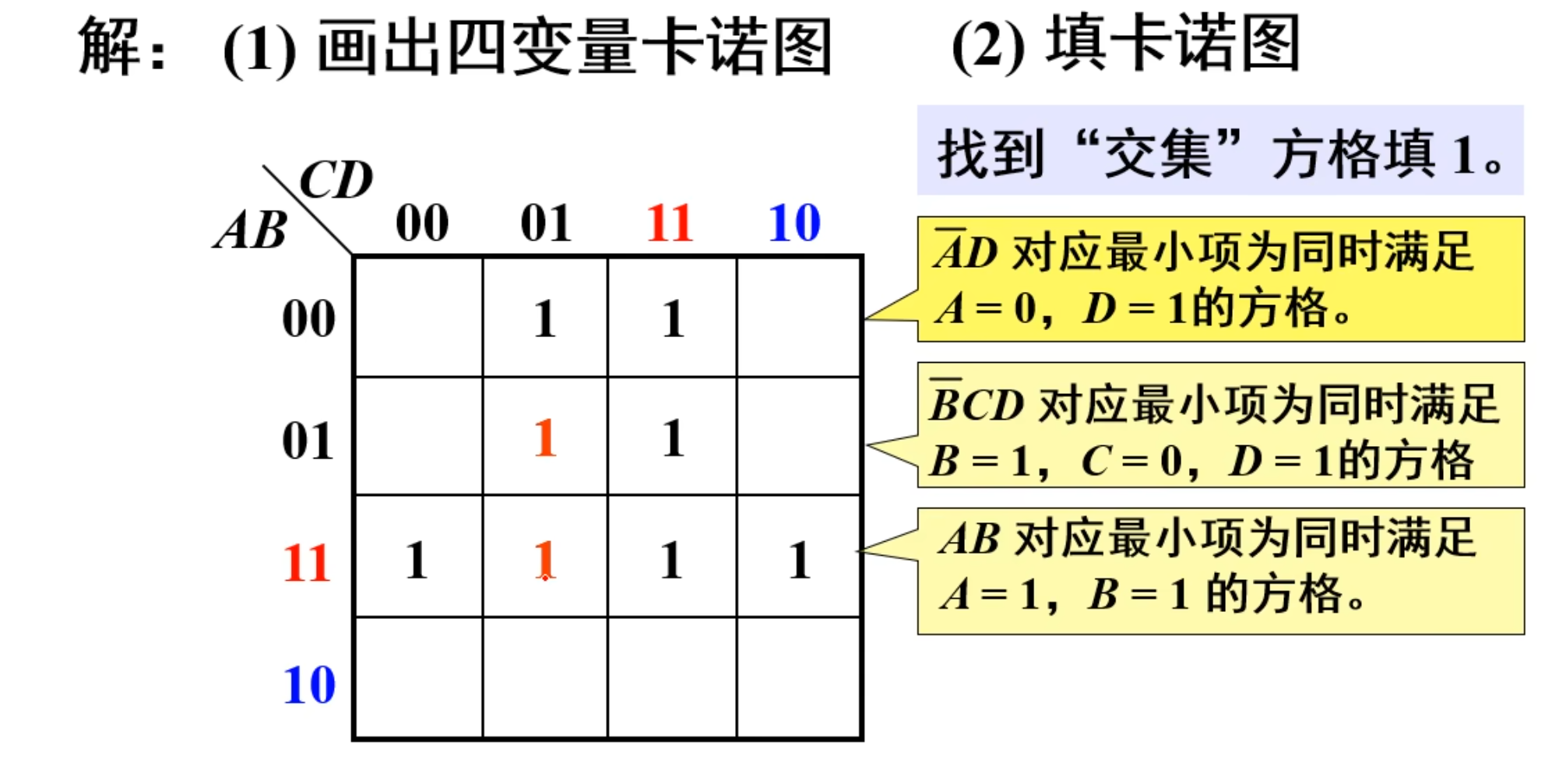
1. 当 2 个小方块相邻（包括处于同一行或同一列的两端），有 1 个变量相异，相加可以消去这一个变量，从而合并为一项

   

   当然，上面这种还需要提取出来计算的方法还是比较慢的，下面的这个方法相对来说是比较快的。

   就是这个口诀是：消异存同

   

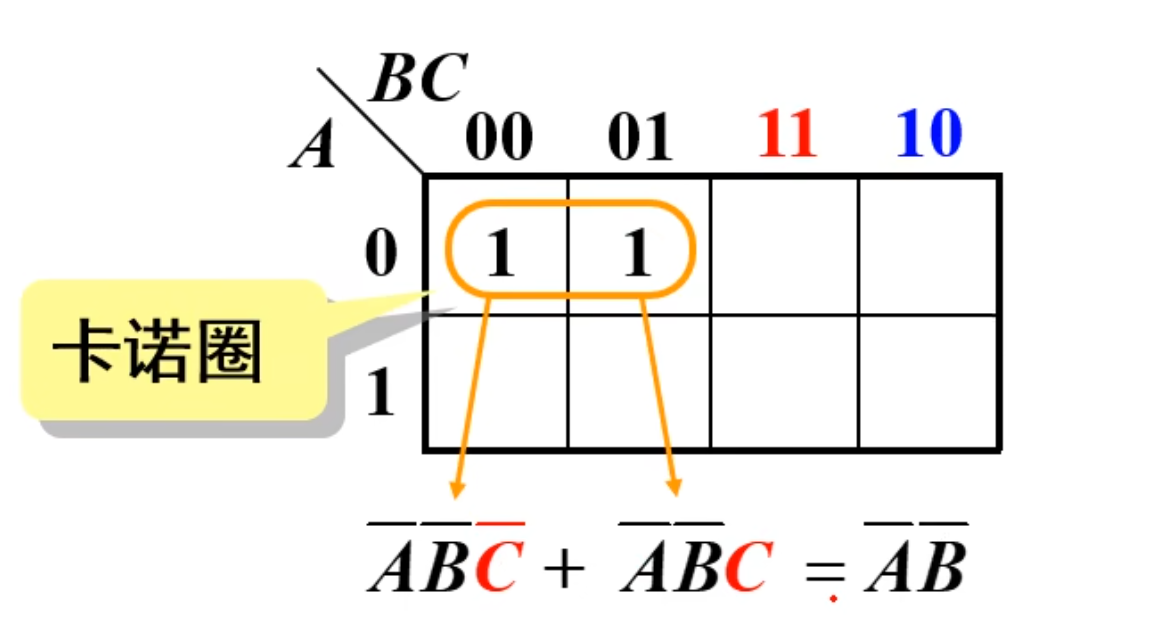
2. 4 个小方块组成一个大方块，或组成同一行/列，或组成两行/列的两端，或处于四个角上，都是可以合并的，消去两个变量

   当然，用到的方法还是消异存同

   

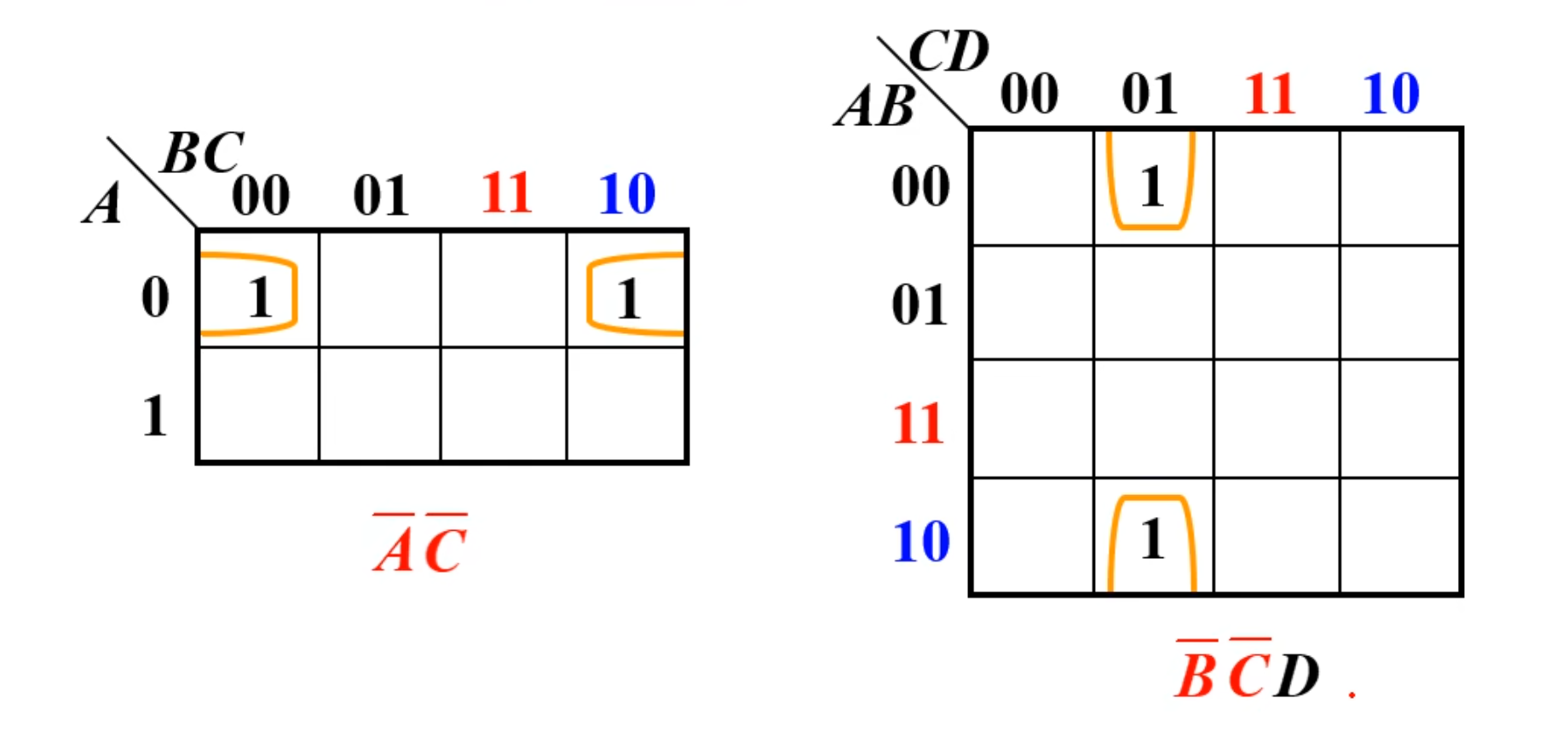
3. 8 个小方块组成两行/列，或组成两边的两行/列，可以合并，消去 3 个变量

   用到的方法也是消异存同

   

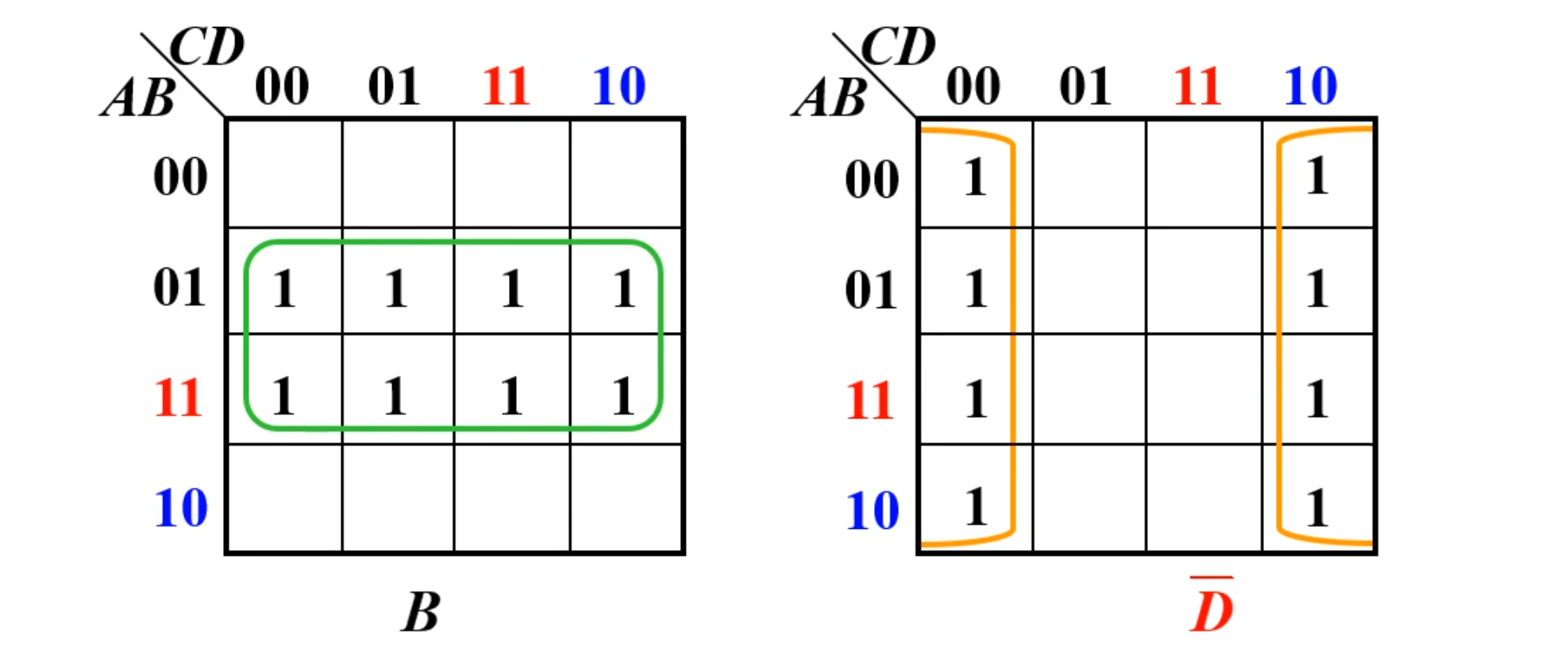
化简步骤

NOTE

首先是画出函数的卡诺图

然后，画卡诺圈，将相邻的 $1$ 方格按照 $2^n$ 圈为一组，直到所有的 $1$ 被圈完

然后，将各个卡诺圈分别化简。

最后，将各卡诺圈的化简结果逻辑加

IMPORTANT

卡诺圈的数量要越少越好，圈越大越好

一个圈中的小方格至少有一个小方格不为其它圈所圈。

直接上例题：

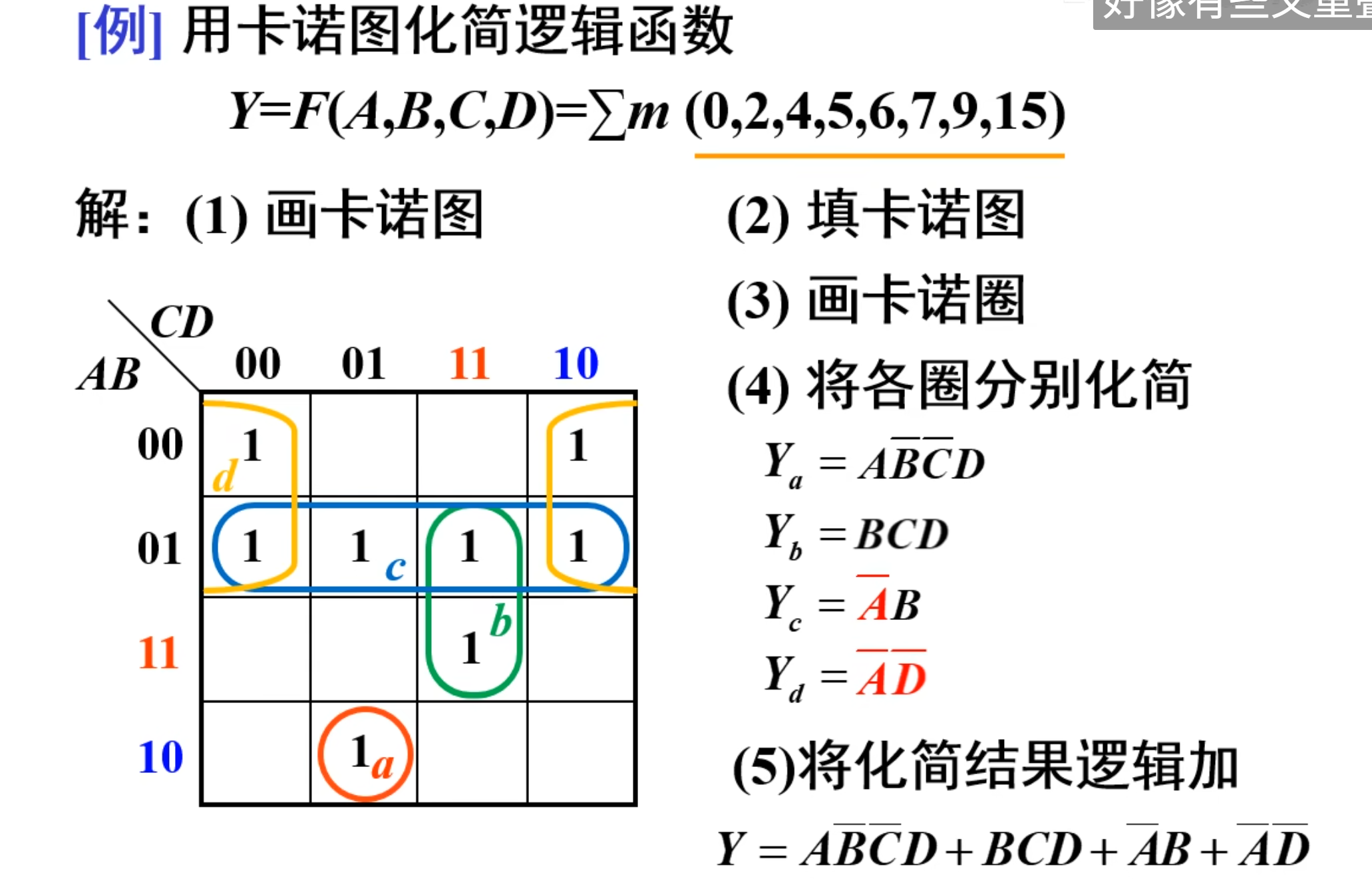
再来一个例题：

上面这题，主要说明的形式是第二个，一个卡诺圈内的 1（变量）至少有一个没有被其他圈给圈起来，这也就导致了中间的哪个大圈其实是多余的。

画卡诺圈规则

1. 每个圈中所包含“1”的小方块数只能为 $2^n$ 个，如 $2、4、8$ ;

2. 画圈的时候，应该将圈画的尽量大，圈数最少

3. 一些为 1 的小方块，可以被圈一次以上

4. 一个圈内至少要有一个之前没有被圈过的 1 的小方块

5. 所有的 1 都要被圈起来，孤立的 1 也不能漏掉

再来几个例题：

特殊情况

有可能出现，多种花圈的方式，进而导致后面的结果也是不一样的。

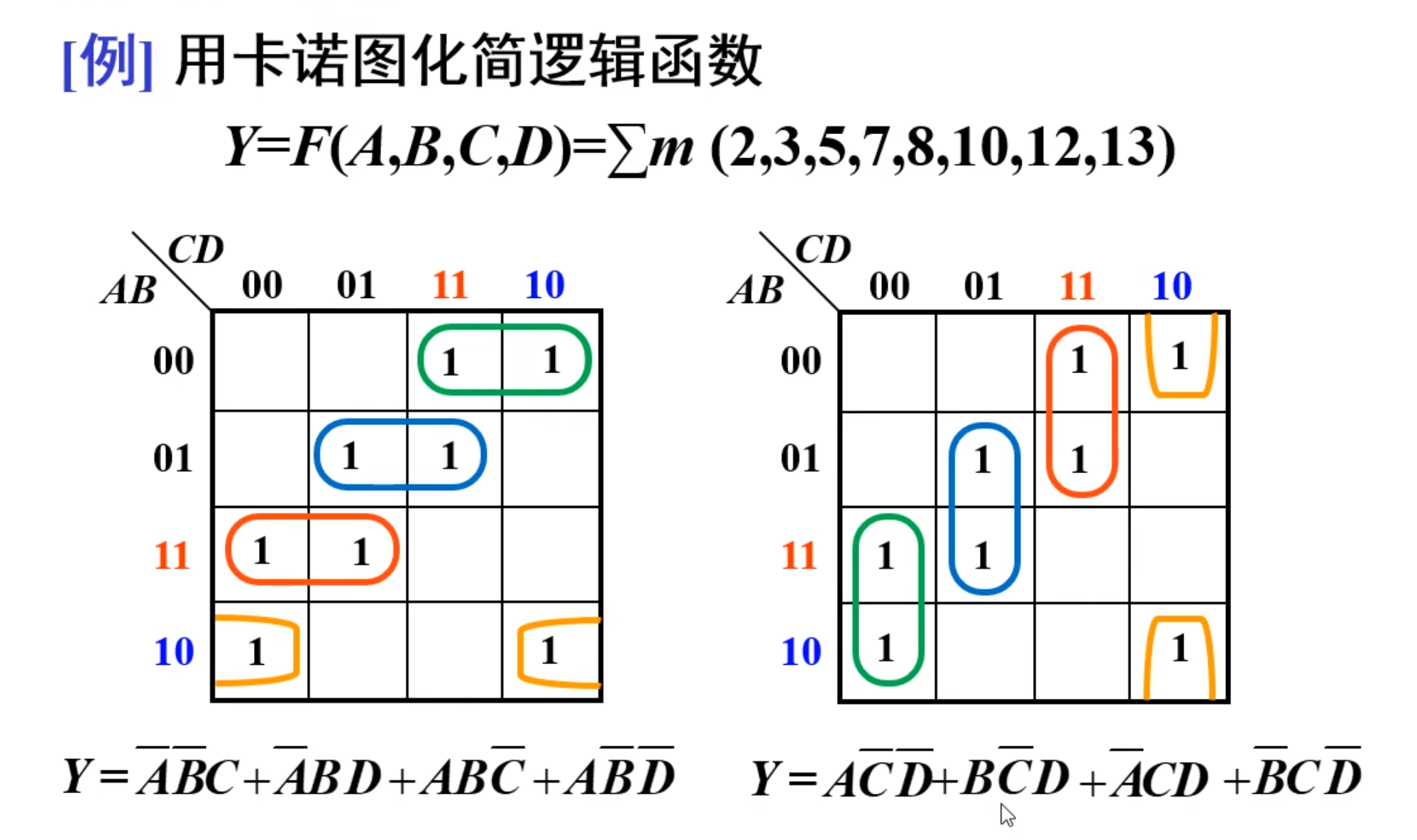
NOTE

逻辑函数化简的结果不唯一

再来一个例题：

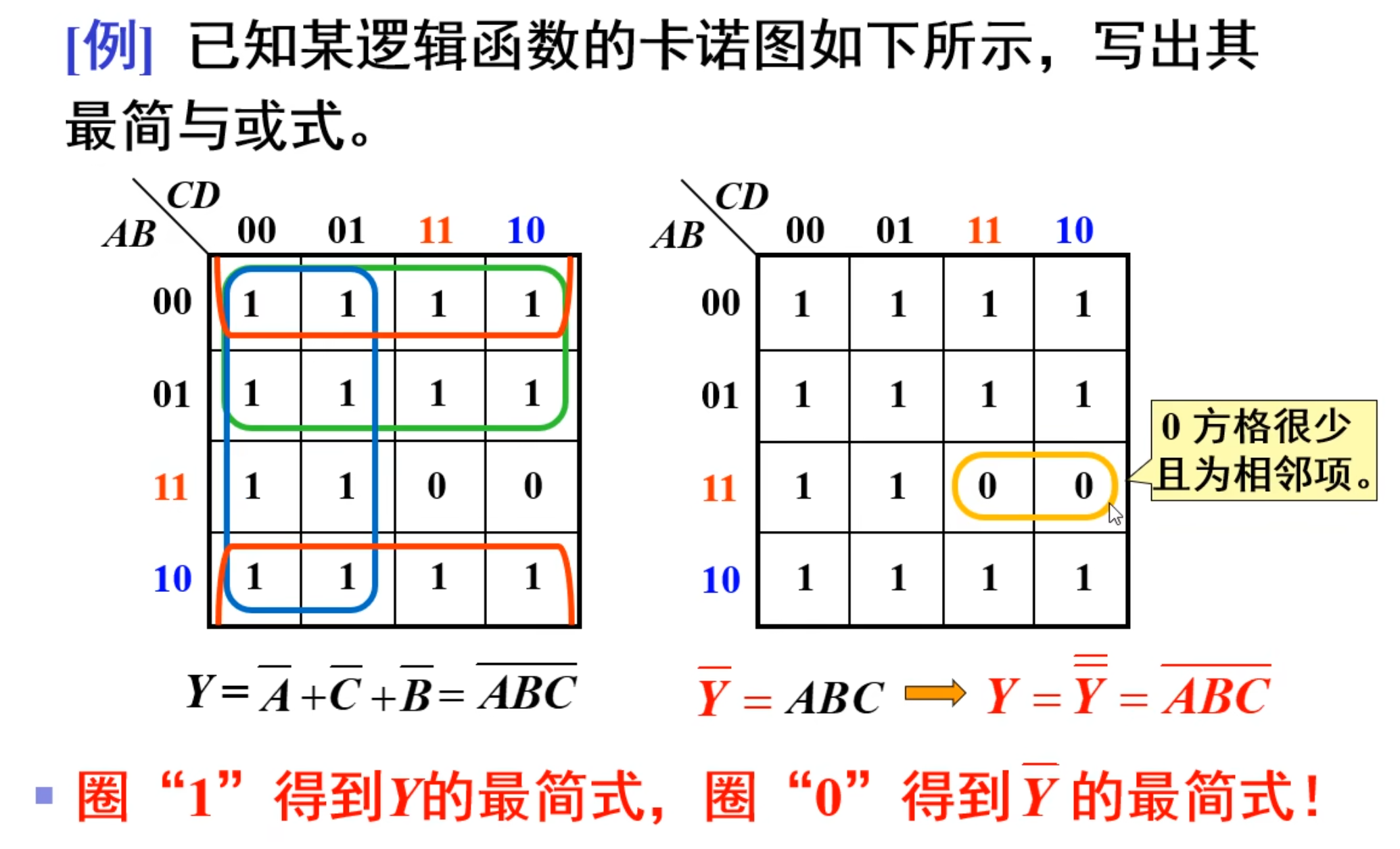
上面这个题目说明，可以使用两种圈卡诺圈的方式来化简。

但是，上面第二种方法中，0 必须是相邻项才行，当 1 比较多的时候，可以考虑

有约束的逻辑函数的卡诺图化简

NOTE

约束条件当作备胎来用，需要的时候就用，不需要的时候就不用。

有些题目中，会提供某些选项不能同时出现，比如说之前 8421 BCD 码，后面 6 种都是约束项，不能同时出现。

而约束条件，用 $d$ 来表示

由于其约束项的值恒为 0，将这些为 0 的最小项加入到逻辑函数与或式中，或者不加进去，都不会影响函数的值，所以在化简的时候将其看成 1 或者 0 都是可以的，使圈最少且最大即可，从而将结果最简。

直接上例题比较好理解：

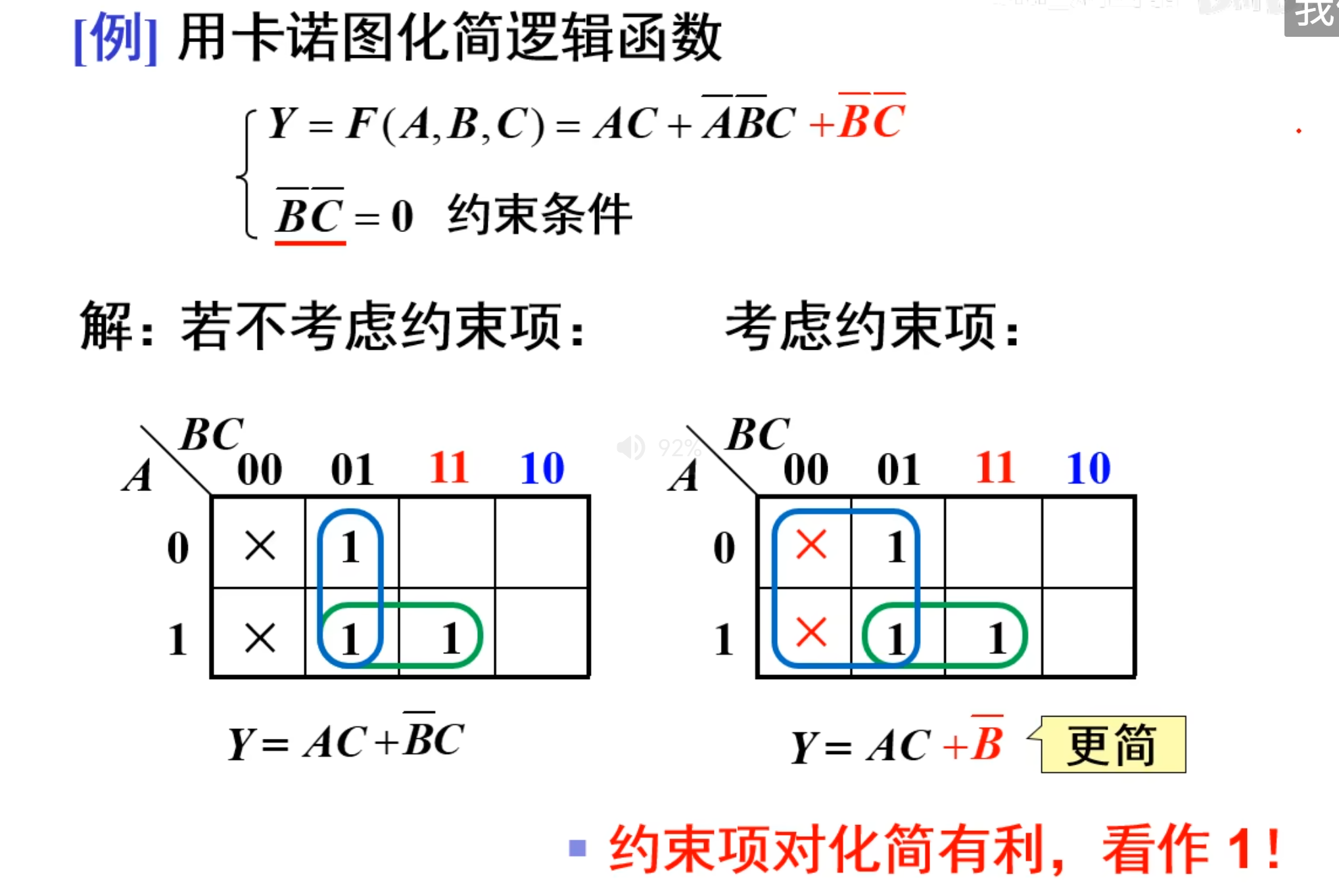
在来一个例题：

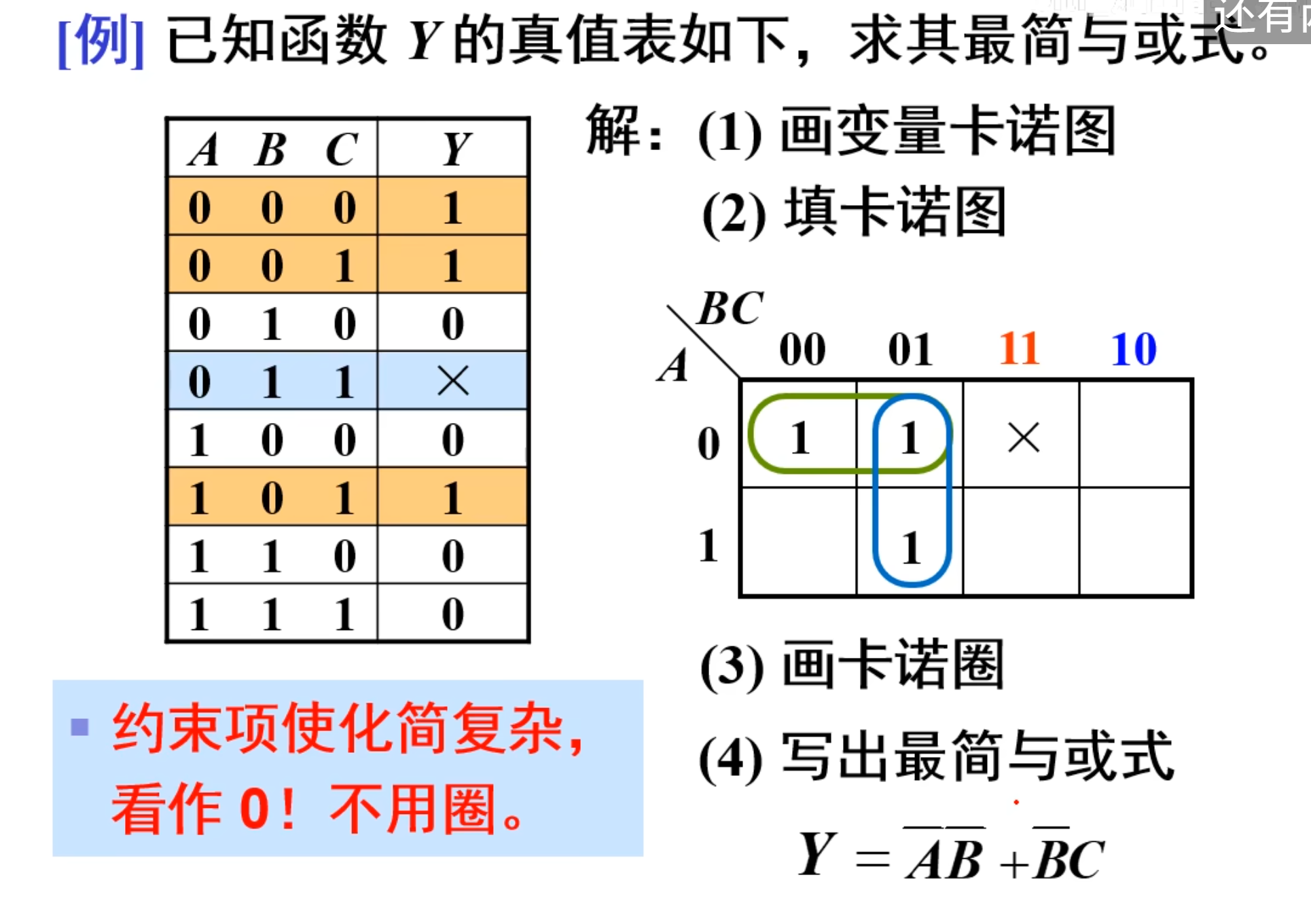
再来例题：

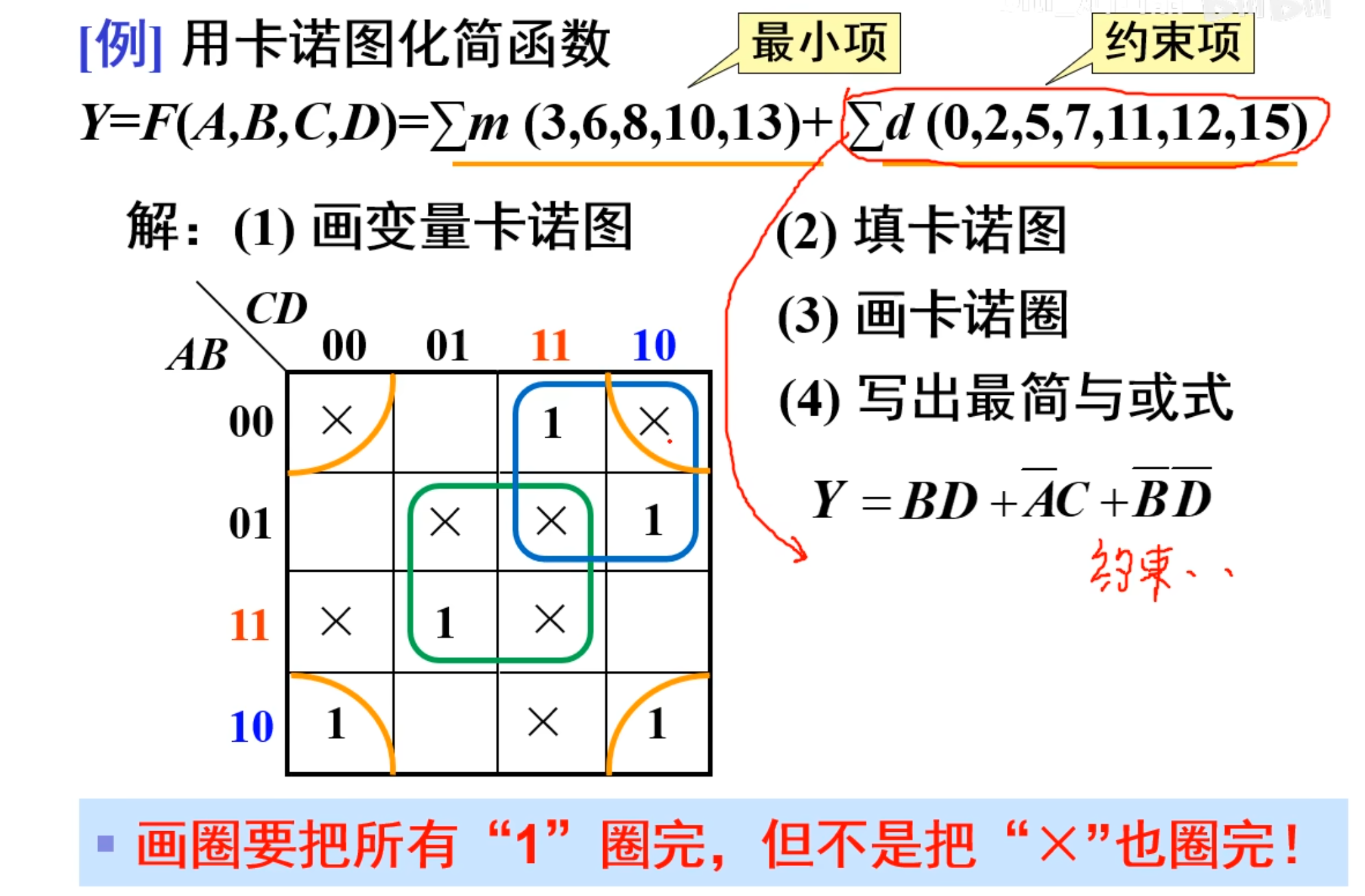
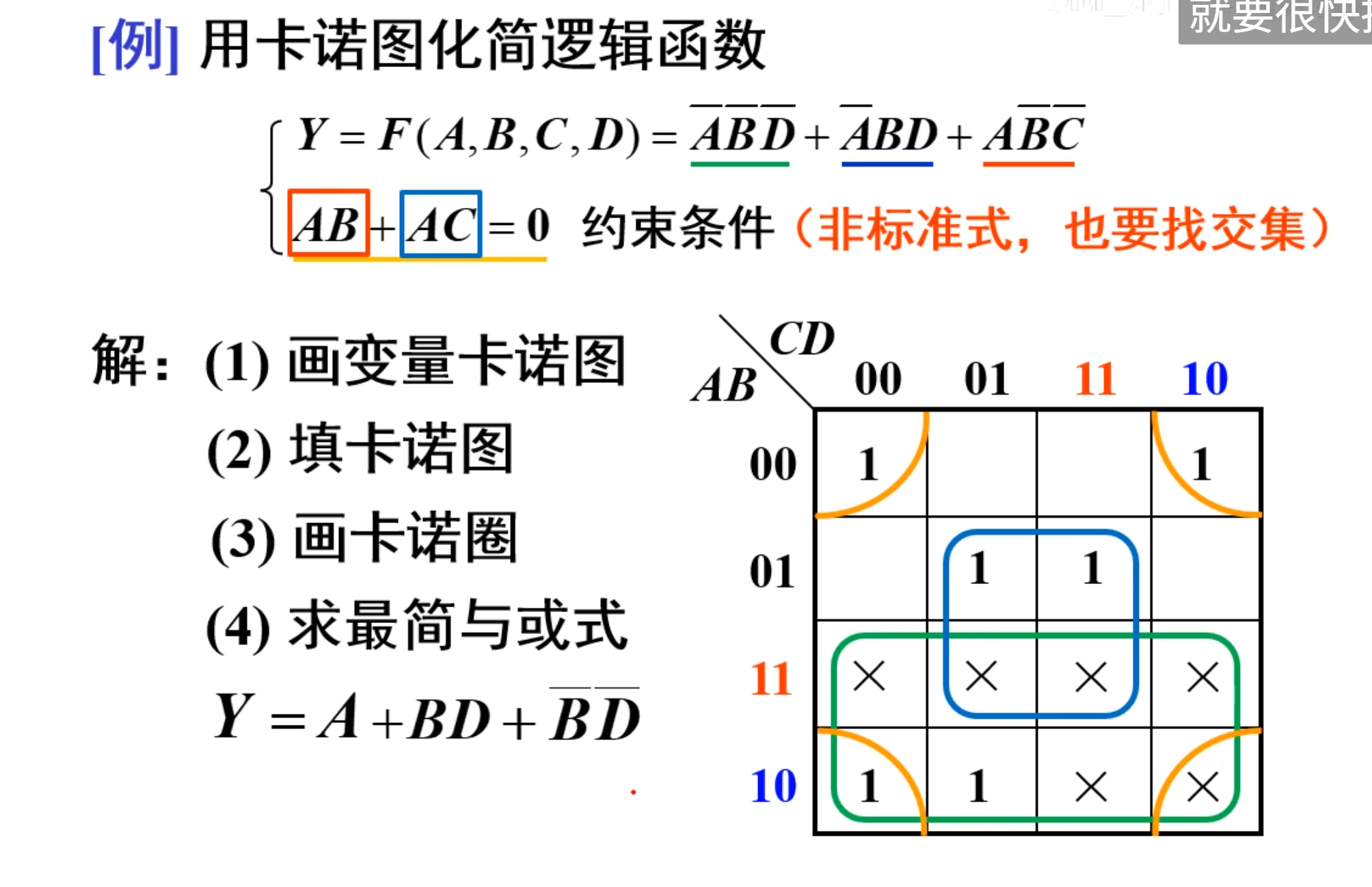
最后一个比较难的题目：

贡献者

王海平

文件历史

最后编辑于 9 天前查看完整历史

28d3e-笔记上传:2025-10-29 16:54:06