字数

1511 字

阅读时间

7 分钟

求函数的单调区间与极值

解题过程和步骤

1. 定义域，任何题目都需要在定义域内
2. 求 $f^{\prime }(x)$；
   1. 寻找定义域内 $f^{\prime }(x)=0$ 的点；（驻点）
   2. 寻找定义域内 $f^{\prime }(x)$ 不存在的点。（不要遗漏）
3. 以上点把定义域分成几部分。
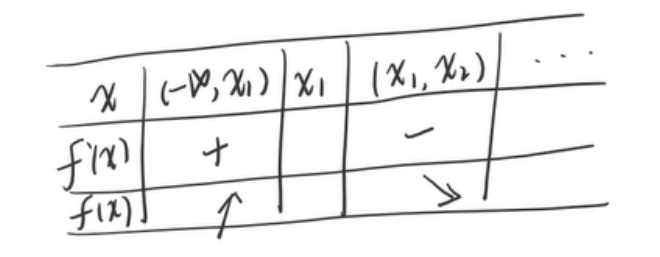
4. 下结论，在什么地方递增，在什么地方递减等。

在求极值的过程中，如果感觉判断左右两边导数值大于 0 还是小于 0 不太好判断，可以使用关于导数、极小值、极大值、拐点之间的关系中的二阶导数来判断（有局限性），具体如下：

若 $f^{\prime }(x_0)=0$ 且 $f^{\prime \prime }(x_0)>0$，则 $(x_0,f(x_0))$ 为极小值点。

若 $f^{\prime }(x_0)=0$ 且 $f^{\prime \prime }(x_0)<0$，则 $(x_0,f(x_0))$ 为极大值点。

解释导数与单调增或减之间的关系

解释为什么 $f^{\prime }(x)>0$ 单调递增， $f^{\prime }(x)<0$ 单调递减：

例题一

$$\text{ 求 }f(x)=(x-4)\cdot \sqrt[3]{(x+1{)}^2}\text{ 的单调区间和极值 }$$

定义域：$(-\mathrm{\infty },+\mathrm{\infty })$。

求导数：

$$\begin{array}{rl}{f}^{\prime }(x)& =\sqrt[3]{(x+1{)}^2}+(x-4)\cdot \frac{2}{3}(x+1{)}^{-\frac{1}{3}}\\ & =\frac{(x+1{)}^{\frac{2}{3}}}{1}+\frac{2}{3}\cdot \frac{x-4}{\sqrt[3]{x+1}}\\ & =(x+1{)}^{\frac{2}{3}}+\frac{2}{3}\cdot (x-4)\cdot (x+1{)}^{-\frac{1}{3}}\\ & =(x+1{)}^{-\frac{1}{3}}\cdot [(x+1)+\frac{2}{3}\cdot (x-4)]\\ & =(x+1{)}^{-\frac{1}{3}}\cdot [\frac{5}{3}x-\frac{5}{3}]\\ & =(x+1{)}^{-\frac{1}{3}}\cdot \frac{5}{3}(x-1)\\ & =\frac{5(x-1)}{3\sqrt[3]{x+1}}\end{array}$$

求完导数，找出导数等于 $0$ 和导数不存在的点，不难发现是 $x_1=1,x_2=-1$。

列表：（做的快，可以不列）核心是看邻域内是正是负，本质是求极限，可以代入特殊值

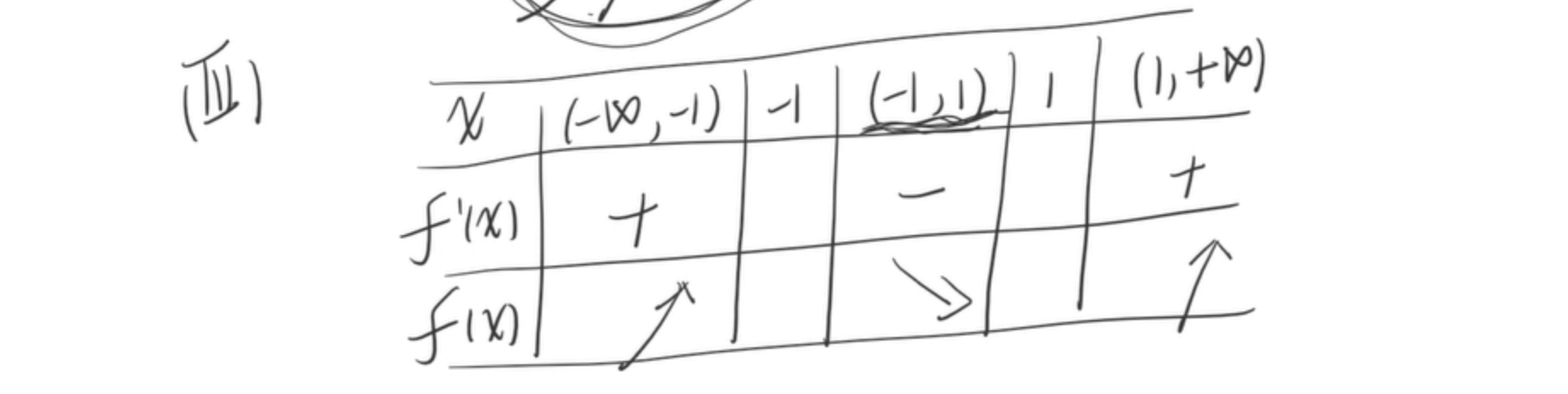
下结论：

$$\begin{array}{rl}& f(x)\text{ 在 }(-\mathrm{\infty },-1),(1,+\mathrm{\infty })\text{ 上单调递增, }\\ & \text{ 在 }(-1,1)\text{ 上单调递减。 }\\ & \text{ 极大植为 }f(-1)=0\text{ ， }\\ & \text{ 极小值为 }f(1)=-3\sqrt[3]{4}\text{ 。 }\end{array}$$

结束。

例题二

$$f(x)=2x^3-9x^2+12x-3$$

定义域是：$(-\mathrm{\infty },+\mathrm{\infty })$

直接求导：

$$\begin{array}{cc}{f}^{\prime }(x)& =6x^2-18x+12\\ & =6(x^2-3x+2)\\ & =6(x-1)(x-2)\end{array}$$

进而得到：

$$x_1=1,x_2=2$$

没有导数不存在的点。

后面直接下结论：

	$(-\mathrm{\infty },1)$	$1$	$(1,2)$	2	$(2,+\mathrm{\infty })$
$f^{\prime }$ (x)	$>0$	$0$	$<0$	$0$	$>0$
$f(x)$	↑		↓		↑

最后的结论略。

证明不等式

直接上例题，通过例题来理解这个应用。

$$\text{当}x>0\text{时，证明}1+\frac{1}{2}x>\sqrt{1+x}$$

解题过程：

$$\begin{array}{rl}\text{证明:令}& f(x)=1+\frac{1}{2}x-\sqrt{1+x}(x>0)\\ & \therefore f^{\prime }(x)=\frac{1}{2}-\frac{1}{2}(1+x{)}^{-\frac{1}{2}}=\frac{1}{2}-\frac{1}{2\sqrt{1+x}}>0\\ & \therefore f(x)\text{在}(0,+\mathrm{\infty })\text{上单增}\\ & \therefore x>0\text{时},f(x)>f(0)\\ & \text{即}1+\frac{1}{2}x-\sqrt{1+x}>0\\ & \therefore 1+\frac{1}{2}x>\sqrt{1+x}(x>0)\end{array}$$

其核心思想主要是证明复合函数的单调性。

当一阶导数求完之后，可能存在无法判断是否大于 $0$，或者小于 $0$，那么这时候就需要求二阶导数，通过凹凸性来辅助判断一阶导数的正负。

判断方程根的个数

IMPORTANT

若 $f^{(n)}(x)\ne 0$ ，则 $f(x)=0$ 至多有 $n$ 个不同根

NOTE

主要思想是利用导数，求出来单调区间以及极值点，根据单调区间与极值点以及单调区间上的极限值。

例如：已知 $x=1$ 为极大值， $f(1)>0$ ，且在 $-\mathrm{\infty }\to 1$ 单调增， $1\to +\mathrm{\infty }$ 单调减。

如果要判断根的个数，只知道单调性是不够的，还需要利用介值定理： 当 $x\to -\mathrm{\infty }$ 的时候，若 $f(x)<0$ ，那么可以知道在此区间内有一个根。

但如果当 $x\to +\mathrm{\infty }$ 的时候，若 $f(x)>0$ ，那么由于两个端点都是大于 $0$ 的，那么在此区间内就没有根

首先是需要先求函数的单调区间与极值

然后是求定义域内 $f^{\prime }(x)=0$ 的点以及 $f^{\prime }(x)$ 不存在的点。（基本上要化简到不能有加减法的地步）

然后求出极大值和极小值来。

紧接着，需要求出函数区间端点上的极限值，如果没有区间，则是定义域端点上的极限值，（特别注意 $\ln x$ ）

用下面这个题来说明：

当 $x>0$ 的时候，方程 $kx+\frac{1}{x^2}=1$ 有且仅有一个根，求 $k$ 的取值范围。

令 $g(x)=kx+\frac{1}{x^2}-1$ ， $g^{\prime }(x)=k-2x^{-3}$ 。

由于 $x>0$ ，所以当 $k\le 0$ 的时候， $g^{\prime }(x)<0$ ， $g(x)$ 单调递减。接下来看两个端点的值：

$$\underset{x\to 0^{+}}{lim}g(x)=+\mathrm{\infty }$$$$\underset{x\to +\mathrm{\infty }}{lim}g(x)<0$$

所以有一个唯一的根。

然后是分析当 $k>0$ 的时候，令 $g^{\prime }(x)=0$ ，得到： $x={\left(\frac{2}{k}\right)}^{\frac{1}{3}}$ 。而在 $0\sim {\left(\frac{2}{k}\right)}^{\frac{1}{3}}$ ，对于 $g^{\prime }(x)=k-2x^{-3}$ 得到： $g^{\prime }(x)<0$ 。（这里需要自行尝试，普遍来说，带入一个在此区间内方便计算的值即可）；

而当 $x>{\left(\frac{2}{k}\right)}^{\frac{1}{3}}$ 的时候， $f^{\prime }(x)>0$ ，也就是说 $x={\left(\frac{2}{k}\right)}^{\frac{1}{3}}$ 是极小值，为：

$$f\left({\left(\frac{2}{k}\right)}^{\frac{1}{3}}\right)=\frac{3-\sqrt[3]{\frac{4}{k^2}}}{\sqrt[3]{\frac{4}{k^2}}}$$

因为是只有一个根，所以，令此最小值等于 $0$ ，得到：

$$k=\frac{2}{3\sqrt{3}}$$

综上所述：

当 $k\le 0$ 或者 $k=\frac{2}{3\sqrt{3}}$ 的时候，方程有唯一根。

再来一个例子：

再来一个例子：

曲率与曲率半径

曲率，主要是用到了与导数相关的知识。

曲率：

$$K=\frac{|y^{\prime \prime }|}{{[1+(y^{\prime }{)}^2]}^{\frac{3}{2}}}$$

曲率半径：

$$R=\frac{1}{K}$$

贡献者

王海平

文件历史

最后编辑于 9 天前查看完整历史

28d3e-笔记上传:2025-10-29 16:54:06